Усні рахунки до теми "Числові нерівності"

 

Алгебра,9 клас

СИСТЕМА УСНИХ РАХУНКІВ  ДО ТЕМИ « ЧИСЛОВІ НЕРІВНОСТІ »

До уроку № 1

1.Чи виконуються такі нерівності:

а)   -8:2<10:(-3);   б) 3 -5< -1 ;   в) 1-1,8:0,04 > -10 ;

г) - >  ;  д) (0,12 -)3 < - 0,2;         е) >0 ?

2.Який знак - > чи < потрібно поставити між дробами   і    , щоб нерівність була правильною?

3.Не обчислюючи, встановіть, чи може значення виразу 1000:390+2 бути розв’яз -ком нерівності х > 5.

4. Які з тверджень правильні:

1) Якщо  -4х  > -8, то х > 2;    2) Якщо  |а|  > 3, то а > 3; 

3) Якщо  х  > у, то  < ;   4) Якщо  х  > у, то2х+0,1 > 2у+0,1.

5) Якщо    > 0, то .

До уроку № 2

1. Які з чисел  3; 3,14;  3,1403; π є розв’язком нерівності х < 3,14.
2. Який знак - > чи < потрібно поставити між виразами|a+b| і   |a|+| b | , якщо а>0,   b <0
3. За якої умови  |a+b| =|a|+| b |?
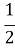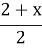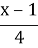4. Розв’яжіть нерівність:   а) 1-х <;   б)-6х <0,3;    в) х +2 <х-4; г) – < 6.

До уроку № 3

1.Використовуючи знак модуля, складіть правильні нерівності, рівносильні нерівностям:  1) -4≤х≤4; 2) -10<х<10;  3) х > 10 і х<10.

2. Зобразити наведені нижче числові проміжки на числовій прямій: а)х Є (-2;2);

б) х Є (-;-6) і (6; );   в) х Є (-10;- 5) і (5; 10 ).

3.Задати наведені вище проміжки за допомогою нерівності, яка містить знак модуля.

4. Розв’яжіть нерівність:   а) 2х- 0,3 >   ;   б) 3х  >6+х ;    в)х (2-х) <2х-1; г)   >0.

До уроку № 4.

1.Функцію  f(x) =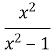 задано на проміжку [-2;2]. Чи для всіх х  з цього проміжку вона існує? Знайдіть проміжки існування функції.

2. Знайдіть найменший натуральний  розв’язок нерівності: а) | - 2| <1;

б)    <0,3; в) | | <1;    г) | | >2;    д)     >29,9.

3. Розв’яжіть нерівність:   а) 2х <-4;   б) 2х+1 <5+3х;    в)   <4; г)   < 0.

4.Перемножте почленно нерівності:  1)  0,04>0,004  і  0,56>0,096

 

До уроку № 5

1. Розв’яжіть нерівність:   а)   - (х-1) <6;   б)5-2х <1-(3+2х);    в)>1;г) |х|≤ 1.

 

2.Точка з координатою а міститься на числовій прямій зліва від точки 0. Порівняйте числа а і 0,00001.

3.Додайте   2     до обох частин нерівності  -5   >-7.

4.Відніміть  -1,02 від обох частин нерівності -1 <0.

До уроку № 6.

1. Розв’яжіть нерівність:  а)  |х|  > 3;  б)   > 1-х ;    в); г) |1-х|≥ 1.

2.Помножте обидві частини нерівності  -1 > -3 на  -2   ; на 5,7.

3.Як на координатній площині зображається множина   розв’язків нерівності

1) –х+3 ≤0 ;  2) 6<-2х.

4.Перемножте почленно нерівності:  1)     >    і   >.

.До уроку № 7.

1. Розв’яжіть нерівність:   а)  |х+|  > 5;  б)   <0 ;    в); г) ах <1-b якщо а <b;   д)  х-1 ≤ 1-   ; е) |х-1|<6

2.Поділіть обидві частини нерівності  0,1 > 0,02 на  -0,01   ; на .

3.У яких межах міститься число , якщо   m< .

4. Перемножте почленно нерівності:  1)    <2    і 2 <2.

До уроку № 9.

1. Розв’яжіть нерівність:   а)1<  - х <2;   б)1 <х-1<3;    в)>1;г) 5≤ 2х+1<6;

 г) 5≤-2х-1≤6;  д) 1,53 ≤ 2-m ≤ 1,54; e)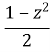 <2.5.

2.Hехай виконуються нерівності  3+а >3+b  i  3+b >3+c,  чи правильно, що  а>с?

3. Перемножте почленно нерівності:  1) -2   <2    і 8  >.

4.За якої умови справджується нерівність: 1) 10-t < 10-k ;    2)8+5b>8+10a;

 3)х-10>у+10;   4)а-10>b-9;    5)(0.1-2.7х)²≥ 0;    6)> .

До уроку № 10

1. Розв’яжіть нерівність:   а)(z-1)(z-2) >0;      б)(n+2)(n-1) <0;        в)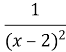>0;

2.Знайдіть ті значення а, при яких мають додатні розв’язки рівняння:

1) ах-2=3х;  2) 5х-3=а;  3) х-ах+а²=1.

3.Розв’яжіть систему нерівностей: 1) х >2 ,         2)       х <10,    3)     х>2.

       х>3;       х<7;        х<3.

4.Знайдіть помилки в міркуванні: Маємо правильну нерівність -1<0. Додавши до обох  її  частин довільне число х, дістанемо  х-1<х. Помноживши обидві частини нерівності на  -х, дістанемо:   -х²+х < -х², звідки х<0.   Отже, будь-яке число від’ємне.

До уроку № 11.

1. Розв’яжіть систему нерівностей: 1)  х-5 >0,         2)     2 х <6,    3)     х>10.

       Х-10 <0;  х >0;           х-2<3.

2.Знайдіть цілі розв’язки нерівності: 1) 4 <х-1 <5;    2)-6 <х+8 <-2;    3) х+5 >х+3.

3.Точка  М лежить всередині квадрата, три вершини якого мають координати 

(-2;1);(-1;1);(-1;2).Назвіть межі координат точки  М.

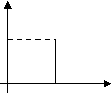
4.На малюнку зображені певні геометричні місця точок координатної площини. Виразити ці місця за допомогою систем рівнянь і нерівностей.

 

 

 

 

До уроку № 12.

1. Розв’яжіть систему нерівностей: 1)  4х-12 >2х+1-, 2)     х <-2,    3)     3х+1>6х-5.

       2Х-6≤ х+5;             х >- 5             1-х<2х+4.

2.Знайдіть цілі розв’язки нерівності: 1) |х|<3;    2) 1≤+3≤5;    3) >0.

3.Маємо системи: 1)   х=0;         2)      у=2;  3) у=0,

      0≤у≤2;      0≤х≤1;            0≤х≤1.

 Що являє собою геометричне місце точок, координати яких задовольняють ці системи?

До уроку № 13.

1. Знайдіть цілі розв’язки систем нерівностей: 1)  х >3;     2)   х≤-10 ;      3)  х≥ 5.

                х <10;       х >-15;         х <7

2. Що являє собою геометричне місця точок,заданих системою:         х ≤6

1)    х =0  2)    у=х-1.   3)   у=х-1   4)       х=2

      0≤у≤1;        0≤х≤1;                  0≤х≤1;          0≤у≤1;