Урок алгебри "Лінійне рівняння"

Рівняння. Лінійні рівняння з однією змінною

Мета уроку: систематизувати відомості про рівняння, корені рівняння; сформувати поняття лінійного рівняння з однією змінною та рівняння першого ступеня з однією змінною; домогтися розуміння учнями алгоритму розв’язування лінійних рівнянь; розвивати пам'ять, логічне мислення, культуру математичних записів.

Очікувані результати: учні повинні розпізнавати лінійні рівняння, наводити приклади лінійних рівнянь, розв’язувати нескладні лінійні рівняння з однією змінною, застосовуючи відповідний алгоритм.

Тип уроку: урок узагальнення й систематизації знань.

■ І. Організаційний етап

Привітання. Перевірка присутності учнів. Перевірка готовності учнів та кабінету до уроку.

■ II. Аналіз контрольної роботи

Оголосити результати контрольної роботи, проаналізувати типові помилки, яких припустилися учні під час її виконання.

■ ІІІ. Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності

▪ Оголошення теми уроку

▪ Формулювання разом з учнями мети й завдань уроку

▪ Мотивація навчальної діяльності

Розв’язання багатьох практичних задач зводиться до розв’язування рівнянь, які можна шляхом певних перетворень звести до вигляду , де a і b — задані числа, x — невідоме. Наведіть приклади таких рівнянь. Сьогодні ви навчитеся розв’язувати нескладні лінійні рівняння з однією змінною, застосовуючи відповідний алгоритм.

■ IV. Актуалізація опорних знань

▪ Виконання усних вправ

1. Спростіть вираз:

а) ;

б) ;

в) .

2. Обчисліть:

а) ;

б) .

■ V. Повторення й аналіз фактів

▪ Бесіда

Орієнтовний перелік питань

1. Означення лінійного рівняння. Приклади.

2. Означення рівняння першого ступеня з однією змінною. Приклади.

3. Кількість коренів рівняння першого ступеня з однією змінною.

4. Кількість коренів лінійного рівняння з однією змінною.

5. Алгоритм розв’язування лінійних рівнянь з однією змінною.

1. Рівняння виду , де a і b — деякі відомі числа, а x — змінна, називають лінійним рівнянням з однією змінною.

Числа a і b називають коефіцієнтами лінійного рівняння.

Наприклад, рівняння , , , — лінійні.

2. Якщо , то рівняння називають рівнянням першого ступеня з однією змінною.

Зверніть увагу, що рівняння , не є рівняннями першого ступеня.

3. Рівняння першого ступеня завжди має тільки один корінь, оскільки поділивши обидві частини рівняння на a, одержимо єдиний корінь цього рівняння: .

4. Для того щоб з’ясувати, скільки коренів може мати лінійне рівняння, розглянемо рівняння:

а) ;

б) ;

в) .

а) Щоб розв’язати рівняння , достатньо обидві його частини розділити на 10. Одержимо єдиний корінь цього рівняння: .

б) Ліва частина рівняння дорівнює нулю для будь-якого числа x, а права частина не дорівнює нулю. Отже, це рівняння коренів не має.

в) Рівність є правильною для будь-якого числа x, тому коренем цього рівняння є будь-яке число (говорять, що рівняння має безліч коренів).

Таким чином, лінійне рівняння може мати один розв’язок, мати безліч розв’язків або не мати розв’язків взагалі.

5. Під час розв’язування лінійного рівняння потрібно дотримуватися певного алгоритму.

Алгоритм розв’язування лінійних рівнянь із однією змінною

1) Якщо в рівнянні є вираз із дробовими коефіцієнтами, то треба помножити обидві його частини на найменший спільний знаменник дробів.

2) Розкрити дужки.

3) Перенести всі доданки, що містять змінну, в одну частину рівняння, а ті, що не містять змінну,— в іншу.

4) Звести подібні доданки й звести рівняння до вигляду .

Схема розв’язування лінійного рівняння

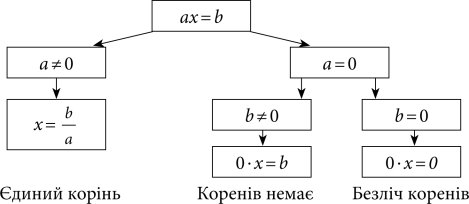
Приклад 1. Розв’яжіть рівняння .

Розв’язання

1) Розкриємо дужки: .

2) Перенесемо доданок x у ліву частину рівняння, а доданок 50 — у праву частину, змінивши при цьому їхні знаки: .

3) Зведемо подібні доданки: .

4) Розділимо обидві частини рівняння на 6: .

Відповідь: –8.

Застосовуючи тотожні перетворення й властивості рівнянь, ми послідовно заміняли одне рівняння на інше, рівносильне йому. Отже, коренем вихідного рівняння є число –8. У цьому прикладі вихідне рівняння було зведено до рівносильного йому лінійного рівняння , у якому коефіцієнт при x відмінний від нуля.

Приклад 2. Розв’яжіть рівняння .

Розв’язання

;

;

;

.

Отримане рівняння не має коренів, отже, рівняння не має коренів.

Відповідь: коренів немає.

Приклад 3. Розв’яжіть рівняння .

Розв’язання

;

;

;

.

Коренем цього рівняння є будь-яке число, отже, і коренем вихідного рівняння є будь-яке число.

Відповідь: будь-яке число.

■ VІ. Удосконалення вмінь

Розв’яжіть рівняння:

а) ;

б) .

в) ;

г) .

№ 47

■ VІІ. Підбиття підсумків уроку

▪ Графічний диктант

Чи є правильними твердження? (Так , ні__.)

1. Рівняння є лінійним.

2. Рівняння має один корінь.

3. Рівняння має безліч коренів.

4. Рівняння не є лінійним.

5. Рівняння не має коренів.

6. Число –1 є коренем рівняння .

Ключ-відповідь:

Запропонувати учням здійснити самоперевірку за ключем-відповіддю, заздалегідь підготовленим на відкидній дошці; відповісти на запитання, що виникли в учнів під час виконання роботи.

 VIII. Домашнє завдання, інструктаж щодо його виконання

§1 повторити, №38, №48