Урок "Арифметична і геометрична прогресії. Історичні задачі."
Тема. Арифметична і геометрична прогресії. Історичні задачі.
Мета : узагальнити і систематизувати знання і вміння по темі „ Послідовності.Арифметична та геометрична прогресії .”;
Повторити вивчені формули та застосування їх до розв’язування задач по темі;
Розвивати логічне мислення учнів, допитливість, потяг до знань;
Виховувати зацікавленість до історії математики.
Тип уроку: узагальнення і систематизація знань.
Твої завдання.
|
Знати: Поняття послідовності; означення арифметичної та геометричної прогресій; формули n –го члена арифметичної та геометричної прогресії та формули суми n – перших членів арифметичної та геометричної прогресії. |
|
Цінувати: Уважність; наполегливість; логічне мислення; набуті знання; час. |
|
Пам’ятка для учня
|
Девіз уроку: недостатньо лише мати гарний розум, головне — це добре застосовувати його.
Р. Декарт
1. Актуалізація опорних знань
Гра „ брейн – ринг”.
( Клас поділено на дві команди. Якщо відповідь готова, то капітан сигналізує хлопком .)
- я задумала арифметичну прогресію. Поставте мені такі два запитання, щоб після відповідей ви могли б назвати швидко сьомий член цієї прогресії.
( а
і d ); ( a
I a
)
- на дошці написано всі натуральні числа від 1 до 50, крім чисел кратних 5. Виберіть із них такі п’ять, які утворили б арифметичну прогресію.
- на дошці написано 20 чисел.
1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55,58. учитель стоїть спиною до дошки. Учні називають номер, а вчитель називає число. Пояснити, як я це роблю.
- задайте арифметичну прогресію з допомогою двох чисел,
причому не можна використати а
і d.
-
(b
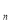) геометрична прогресія, у якій b
= 2. знайдіть такий
знаменник, щоб 120< b
<130.
підсумок гри та визначення команди – переможниці.
2. Мотивація навчальної діяльності.
До сьогоднішнього уроку ви, користуючись додатковою літературою, виписали приклади історичних задач на прогресії.
Оголошую конкурс на найдавнішу задачу.
3. Конкурс історичних задач
(учень представляє задачу та її розв’язок)
№1
|
Сто мір хліба слід розділити між п’ятьма людьми так, щоб другий одержав на стільки ж більше від першого, на скільки третій одержав більше від другого, четвертий більше від третього і п’ятий від четвертого. Крім того, двоє перших повинні одержати в 7 разів менше за трьох інших. Скільки потрібно дати кожному. |
Ця задача записана в єгипетському папірусі Рінда, яка відноситься, можливо до ІІІ століття до нашої ери.
Розв’язування:
(a
) –арифметична прогресія
S
= 100 мір
( a
+ a
)* 7 = a
+ a
+ a
( a
+ ( a
+ d ))* 7 = ( a
+ 2d)*( a
+3d)
S= 
14a
+ 7d = 3a + 9d
100= 
11a
= 2d
20 = a
+ 2d d = 
a
a
= 20 – 2 *
a
; 20 = 12 a
; a
=
= 
;
d= 
*
= 9
a
= 
+9
= 1
+9=10
; a
= 10 + 9= 20
a
=20 + 9= 29
a
= 29+ 9 =38 
.
Отже, 100 мір хліба було розділено таким чином
1; 10; 20; 29; 38 .
№ 2
|
10 мір ячменю розділили між 10 людьми так, щоб кожний наступний одержав на (папірус Ахмеса) |
міри більше від попереднього
Розв’язування:
S = 10мір.
d =
S
= 
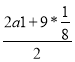10 =
*10
2=2a
+ 
2a= 
a
= 
.
Отже, кожен отримає: 
;
;
;
;
;
;
;
;
;
мір ячменю.
№3
|
10 братів; 1 |
міни срібла; брат над братом піднімається, на скільки піднімається— я не знаю. Частка 8-го — 6 шенкелів. На скільки брат над братом піднімається
Розв’язання:
1 міна = 60 шенкелів
(а
) – арифметична прогресія
n = 10; S
= 1
міни = 100 шенкелів
a
= 6
S= 
; 100 =;
або
20 = 2a
+ 9d
6 = a
+ 7d
8 = - 5d; d = -
= - 1
a
= 6-7d = 6 + 7 * 
= 6 + 
= 6 + 11
= 17
a
= 17- 1 = 15
і т. д.
Отже, брат над братом піднімається на -1
№4
|
Задача Феофана Прокоповича Якась людина має багато коней, і всім їм різна ціна. Найгірший кінь коштує 4 золотих, а найкращий 55 золотих, і ціна від одного до другого коня весь час піднімається на 3 золотих. Питаємо: скільки всього було коней? |
Розв’язання
a
= 4; d = 3; a
= 55; n - ?
a= a+ (n -1)d
55 = 4 + (n – 1)*3
51 = (n – 1)* 3
n -1 = 17
n = 18
Відповідь: 18 коней.
Історична довідка
У перекладі з латинської слово „прогресія” означає рух вперед. Прогресії відомі здавна, а тому не можна сказати, хто їх відкрив. Адже і натуральний ряд 1, 2, 3, 4, ....— це арифметична прогресія, в якій а
= 1,
d = 1.
Під час розкопок у Єгипті було знайдено папірус, що датується 2000 роком до нашої ери, але і його було переписано з іншого, ще давнішого, віднесеного до ІІІ тисячоліття до нашої ери. Учені розшифрували текст папірусу і прочитали кілька задач. Зміст деяких з них дає можливість віднести їх до задач на прогресії. Про те, як давно була відома геометрична прогресія, свідчить і легенда про історію винайдення шахів.
Винахідник шахів за свій винахід попросив винагороду:
„ за першу клітинку шахової дошки поклади одну зернину пшениці, за другу — дві, за третю — чотири, за четверту — вісім і так до 64 клітинки поля?” . Індійський принц Сірам розсміявся, коли почув таке прохання.
S = 1+ 2+ 2
+ 2
+ … + 2
= 2
– 1= 188446744073709551615
Таку кількість зерна можна зібрати з площі, у 2000 разів більшої від усієї поверхні землі.
Задачі на прогресії зустрічаються в одній з найдавніших пам’яток „Руській правді”, укладеній ще за часів Київського князя Ярослава Мудрого (11 ст.)
Значна кількість задач на прогресії є в арифметиці Л. Магницького (1703 рік), що була основним підручником в Росії протягом майже півстоліття.
Бачимо, що перші із задач на прогресії, які дійшли до нас, пов’язані із запитами господарського життя і суспільної практики, як, наприклад, розподіл продуктів та спадщина, одержання винагороди тощо.
Розглянемо задачі із „ арифметики „ Л. Магницького.
(Продовження конкурсу)
№ 5
|
У семи осіб сім кішок, кожна кішка з’їдає по сім мишей, кожна миша з’їдає по сім колосків ячменю, із кожного колоска може вирости по сім мір зерна. Скільки мір зерна збережеться завдяки цим кішкам? Єгипетський папірус— близько 2000 років до н. е. |
Розв’язання
а= 7; g = 7; n = 5; (a
) — геометрична прогресія
а
= 7 * 7
= 7*7*7*7*7= 49*49*7= 16807 мір зерна.
№6
|
Дехто хотів підкувати свого коня і звернувся до коваля з проханням взяти з нього подешевше. Коваль запропонував: „Заплати мені тільки за цвяхи, яких я затрачу 24 штуки. За перший цвях заплати мені |
Розв’язування
( b
) — геометрична прогресія
b
= 
; b
=
; b
= 
1, і т. д
b
— знайти
b= b* g
= *2
= 
* 2= 2
=2
*2*2= 1024 *1024 *2 20971 р.52 коп
№7
|
Дехто продає свого коня по кількості цвяхів у підковах, яких у нього 16. за перший цвях він просить 1 к, за другий 2 к, за третій —4 к., за четвертий —8 к, і завжди за кожен наступний вдвоє більше, ніж за попередній. Питається: за скільки він цінить коня? |
Розв’язування
( b) — геометрична прогресія;
b
=1; g = 2; n = 16;
S
=
; S= 
= 2
- 1 = 65536 – 1= 65535 =655 руб. 35 коп.
№ 8
|
Мешканець маленького містечка був відомий своєю скнарістю. Коли в нього були справи в повітовому місті, розташованому в 25 км. від цього містечка, він шукав сусідів, які підвезли б його додому. Одного разу скнара крутився на площі, шукаючи того, хто підвіз би його „ за спасибі” додому. Але цього разу нікого не було і він змушений був шукати платного візника. Скнара обійшов їх усіх, торгуючись з ними і порівнюючи ціни. Один просив 250 грн., другий — 200грн., третій — 150грн. Усі ці ціни здались йому занадто високими. Нарешті він помітив візника з убогим візком і жалюгідною шкапою. Коли скнара запитав його скільки він візьме за дорогу, той подививсь на землю, почухав потилицю і відповів: „за 1-й кілометр заплатите мені 1 коп., за 2-й — 2 коп., за 3-й — 4 коп., за 4-й — 8 коп., і так до кінця шляху. |
Розв’язування
S
=
= 2 b
- 1. b= b
* g
= 1* 2
S= 2 * 2
- 1 =2
- 1 = 3355431 коп. =335544 грн. 31 коп.
4.Підсумок уроку.
- Чи досягнута мета нашого уроку?(висловлення учнів)
- Яку літературу ви використали при підготовці до уроку.
- Яка задача найдавніша?(задача з єгипетського папірусу Рінда)
5. оцінювання учнівських робіт.
про публікацію авторської розробки
Додати розробку