Урок «Діаграма Венна. Знаки "належать", "не належать"».

Урок 4

Тип урока: ОНЗ.

Тема: «Диаграмма Венна. Знаки  , ».

 

Основные цели:

1) сформировать умение схематически изображать множества с помощью диаграмм Венна, использовать знаки ,  для обозначения принадлежности элементов множеству;

2) повторить свойства множеств, способы их задания, обозначение элементов множе-
ства;

3) тренировать навыки устных вычислений и умение с помощью символов записывать предложения; навыки составления буквенных выражений по тексту задач.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение.

Демонстрационный материал:

1) эталон способов задания множеств (из урока № 2, Д-6);

2) набор для оформления макета зоопарка — дерево, тропинки, «заборчик» в виде замкнутой кривой линии;

3) карточки для доски:

 

                                                                                                         — 3 штуки   

 

4) двухсторонние карточки для доски с изображениями животных и чисел:

38 — тигр, 250 — обезьяна, 11 — жираф, 357 — Чебурашка

5) карточка для этапа актуализации:

 

 

 

 

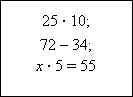
6) карточка с понятием замкнутая линия:

 

 

7) карточки с шагами плана:

1) Используем замкнутую линию для изображения схемы

2) Расположим элементы множества внутри замкнутой линии.

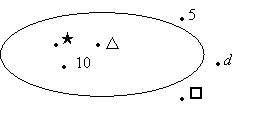
3) Ответим на вопросы: 1. Является ли т элементом множества Z?

                                                2. Является ли о элементом множества Z?

                                                3. Является ли ж  элементом множества Z?

 

4) Выделим в вопросах общую часть (?) и заменим одним словом (?).

5) Заменим это слово математическим символом.

 

8) опорный конспект изображения множеств:

 

 

 

 

 

 

9) эталон для самопроверки к самостоятельной работе.

№ 2, стр. 10

b  A e  A   A

8  A 4  A   A

№ 3, стр. 10

 

 

 

        

 

Справа от решения № 2 и № 3 со стр. 10 вывешивается опорный конспект (эталон) из Раздаточный материал:

1) планшетки;

2) значок             — подарок для каждого ребенка.

 

 

3) карточки для рефлексии (из урока № 1, Р-2.)

 

Ход урока:

 

1. Мотивация к учебной деятельности.

Цель:

1) мотивировать к учебной деятельности посредством вовлечения детей в игру - путешествие «Зоопарк»;

2) определить содержательные рамки урока: множества;

3) организовать актуализацию требований к ученику со стороны учебной деятельности.

 

Организация учебного процесса на этапе 1.

На доске карточки с числами, в стороне — заборчик, похожий на замкнутую кривую линию, над ним надпись «ZOO».

•      Ребята, вы любите ходить в зоопарк? (…)
•      Почему вам это нравится? (…)
•      Назовите одним словом тех, кто живёт в зоопарке. (Животные.)
•      Как математическим языком назвать животных, собранных вместе? (Множество животных).

Если дети затрудняются, учитель предлагает вспомнить тему прошлых уроков.

•      Сегодня вы совершите прогулку по зоопарку, это поможет вам повторить тему «Множества» и узнать что-то новое.
•      Давайте вспомним как вы узнаёте новое ?( … )
•      Готовы отправляться в путь?
•      Желаю вам интересного путешествия!

2. Актуализация знаний и фиксация затруднения в пробном действии.

Цель:

1) повторить задание множества перечислением элементов; актуализировать знания о свойствах множеств;

2) уточнить представления о замкнутых и незамкнутых линиях;

3) мотивировать к пробному действию, организовать его самостоятельное выполнение;

4) зафиксировать индивидуальное затруднение в изображении схемы множества Z или в обосновании этой схемы.

Организация учебного процесса на этапе 2:

1) Тренировка навыков устных вычислений, способности к символьной записи предложений, тренинг мыслительных операций.

•      Перечислите животных, которых вы видели в зоопарке? (…)
•      Чтобы познакомиться с обитателями нашего зоопарка, нужно выполнить задания. Приготовьте свои планшетки. Я буду читать предложения, а вы записывайте их на математическом языке: число 25 взяли слагаемым 10 раз; уменьшаемое 72, вычитаемое 34; задуманное число увеличили в 5 раз и получили 55.

Учащиеся записывают на планшетках: 25 ∙ 10; 72 – 34; х ∙ 5 = 55.

Выполнение задания проверяется фронтально. Если некоторые дети запишут первое предложение в виде суммы, можно обсудить преимущества другого способа записи. Согласованный вариант выносится учителем на доску.

 25 ∙ 10;

 72 – 34;

 х ∙ 5 = 55

•      Вычислите устно значение первого выражения. Что получилось? (250.)

Учитель предлагает одному из учащихся выйти к доске и выбрать карточку с этим числом.

•      Кто изображен на обратной стороне карточки? (Обезьяна.)
•      Пригласим ее жить в наш зоопарк.

Учащийся помещает карточку с изображением обезьяны на часть доски, ограниченную «заборчиком». Аналогично проводится работа с выражением 72 – 34 и с уравнением х ∙ 5 = 55.

Таким образом зоопарк «заселяется» животными: обезьяной, жирафом и тигром. На доске остается карточка с числом 357.

•      Обратите внимание на оставшуюся карточку. Какое число записано? (357.)
•      Расскажите об этом числе. (Это число трехзначное, нечетное, записано цифрами 3, 5, 7…)
•      Посмотрим, кто изображен на обратной стороне карточки.

Учитель снимает с доски карточку и демонстрирует классу картинку с изображением Чебурашки.

•      Чебурашка живет в зоопарке? (Нет, это сказочный герой, придуманный Э. Успенским.)

Учитель карточку с изображением Чебурашки помещает на прежнее место (вне зоопарка).

 

2) Повторение способа задания множества перечислением элементов.

•      Запишите в рабочих тетрадях множество животных, живущих в нашем зоопарке. Как это сделать? (Нужно в фигурных скобках перечислить элементы множества.)
•      Удобно записывать элементы словами? (Нет.)
•      А как удобно? (Заменить слова отдельными буквами, например обезьянка — о; жираф — ж и тигр — т.)
•      Нужно дать имя множеству? (Да.)
•      Договоримся назвать множество латинской буквой Z — начальной буквой английского слова ZOO, что в переводе на русский язык означает зоопарк. Запишите множество Z перечислением его элементов.

Дети работают в тетрадях. Возможно, записи детей будут отличаться порядком перечисления элементов в множестве. Учитель открывает на дополнительной доске один из возможных вариантов записи:

 Z = {ж, т, о}

3) Повторение основных свойств множеств.

•      У кого есть другой вариант записи? (…)
•      Чем отличается ваша запись? (Другая последовательность записи элементов в множестве.)
•      Почему у вас получились разные варианты? Кто прав? (Все, так как порядок перечисления элементов множества значения не имеет.)
•      Элементы в множестве Z повторяются? (Нет, все элементы различны.)
•      Итак, перечислите основные свойства множеств. (Все элементы собраны вместе, ни один из них не повторяется и порядок записи элементов не важен.)

На дополнительную доску выставляется соответствующий эталон Д-1.

•      Давайте обозначим это множество.

Вместо надписи ZOO на доску помещаются карточки: 

4) Уточнение представлений о замкнутых и незамкнутых линиях.

•      Давайте посадим дерево, выложим тропинки.

Кто-то из ребят выходит к доске и дополняет макет зоопарка, прикрепляя внутри замкнутой линии дерево и тропинки:

 

 

 

 

 

•      Чем отличается линия-граница зоопарка от линий-тропинок? (Первая — замкнутая, а две другие — незамкнутые.)
•      Какая линия называется замкнутой? (Линия, у которой начало и конец совпадают.) – правило фиксируется на доске.
•      Что вы сейчас повторили? (Способы задания множеств, основные свойства множеств, запись предложений математическими символами, определение замкнутой и незамкнутой линий).
•      Для чего вы это всё повторили ? (Нам это пригодится сегодня на уроке.)
•      Что я вам сейчас предложу ? ( … )
•      Итак, готовы ? ( … )

5) Задание для пробного действия:

Изобразите схематически на планшетах множество обитателей зоопарка Z. Для этого элементы множества, обозначенные строчными буквами вам нужно расположить на вашем рисунке. Порядок расположения имеет значение? (Нет.)

Подумайте, как показать, что животных собрали вместе - они образуют множество.

Это задание вам нужно выполнить за 1 минуту.

Дети пытаются выполнить задание.

-Стоп, время истекло! Положите маркеры. Покажите мне и друг другу, что у вас получилось.

- Дети, кто не построил схему множестваZ ? В чём ваше затруднение? (Я не смог построить схему множества Z.)

- Ребята я вижу несколько разных схем множества обитателей зоопарка, покажите эталон которым вы воспользовались, выполняя задание, а другими словами обоснуйте свой выбор. (У нас нет эталона, и мы не можем обосновать).

- Так что же делать дальше? (Остановиться и подумать.)

 

3. Выявление места и причины затруднения .

Цель:   

1) организовать восстановление выполненных операций;

2) организовать фиксацию места (шага, операции), где возникло затруднение;

3) организовать соотнесение своих действий с используемыми эталонами (алгоритмом, понятием и т.д.).

На этой основе организовать выявление и фиксацию во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостает для решения исходной задачи и задач такого класса или типа вообще.

 

Организация учебного процесса на этапе 3:

- Какое задание выполняли? (Создавали схему множества Z.)

- Где возникло затруднение ? (В оформлении схемы, в обосновании построенной схемы).

- Почему вы не справились с заданием? (У нас нет эталона, который смог бы нам помочь.)

4. Построение проекта выхода из затруднения.

 Цель:

Организовать построение проекта выхода из затруднения:

1) учащиеся ставят цель проекта;

2) учащиеся уточняют и согласовывают тему урока;

3) учащиеся определяют средства (алгоритмы, модели, справочники и т.д.).

4) учащиеся формулируют шаги, которые необходимо сделать для реализации поставленной цели.

 

Организация учебного процесса на этапе 4.

- Значит какую цель вы поставите сегодня на уроке? (Получить эталон для построения схемы и научиться строить схему любого множества.)

- Хорошо. Как сформулируем тему урока? (Выслушиваются варианты детей.)

- Давайте договоримся, что в процессе работы более точно сформулируем тему урока.

- Что, из того, что вы сегодня повторяли, вам может помочь? (Замкнутые линии, свойства задания множеств.)

- Составим план действий.

- Что вам поможет изобразить элементы множества Z = {т, о, ж} в рисунке? (Замкнутая линия.)

1) Используем замкнутую линию для изображения схемы.

- Так как элементы множества «собраны вместе», где мы их расположим на схеме?

2) Расположим элементы множества внутри замкнутой линии.

3) Ответим на вопросы: 1. Является ли т элементом множества Z?

                                            2. Является ли о элементом множества Z?

                                            3. Является ли ж элементом множества Z?

4) Выделим в вопросах общую часть (?) и заменим одним словом (?).

5) Заменим это слово математическим символом.

 

5. Реализация построенного проекта .

Цель:

1) организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний;

2) организовать согласование способов и фиксацию построенного способа действия в речи и знаково (с помощью диаграммы Венна и знаков   и );

3) организовать уточнение общего характера.

 

Организация учебного процесса на этапе 5:

- Сейчас вы будете работать в группах по составленному плану Какие правила работы нужно соблюдать, работая в группе? (Карточка с правилами находится у каждого учащегося в опорных конспектах или на стенде в классе.)

правила работы в группе:

* В группе должен быть организатор обсуждения.

* Каждый может высказать свою версию решения.

* Один говорит, остальные слушают и пытаются понять.

* Каждая версия обсуждается в группе.

* В группе согласуется  общее решение.

* Представитель группы защищает согласованное решение перед классом.

Дети объединяются в группы и реализуют шаги плана.

Представитель одной группы обобщает работу своей группы, остальные работают на дополнение.

- Вы получили схему зоопарка. Давайте посмотрим, отражены ли на ней свойства множества? (Да, элементы собраны вместе, повторений нет, порядок расположения не важен.)

Графическое изображение множеств, с которым вы только что познакомились, придумал английский ученый-математик Джон Венн, поэтому их называют диаграммами Венна.

Учитель прикрепляет карточку:  

 

 

Если пункты 3 и 4 плана вызвали затруднение, то оно снимается посредством диалога.

- Является ли т элементом множества Z? (Да.)

- Скажите полным ответом. (Тигр является элементом множества Z).

- Является ли о элементом множества Z? (Да.)

- Скажите полным ответом. (Обезьяна является элементом множества Z).

- Является ли ж элементом множества Z? (Да.)

- Скажите полным ответом. (Жираф является элементом множества Z).

- Хорошо.

- Выделите в этих предложениях общую часть. (Общая часть этих предложений — слова «является элементом».)

- Чем обычно пользуются при замене длинных текстов в математике? (Знаками, терминами.)

- В данном случае вместо слов «является элементом» говорят «принадлежит». Так, например, вместо предложения «Обезьяна является элементом множества Z» принято говорить «Обезьяна принадлежит множеству Z».

Учитель закрывает словосочетания «является элементом» карточками со словом «принадлежит»:

Обезьяна множеству Z.

Тигр множеству Z.

Жираф множеству Z.

 

- В математике вместо многих слов используют различные символы. В математике есть знак, который заменяет слово «принадлежит», откройте учебник на стр. 10 и посмотрите на него.

Дети открывают учебник и знакомятся с общепринятым обозначением. Учитель помещает на доске карточки со знаками   и , уточняя формулировку темы урока:

- Тема урока: «Диаграмма Венна. Знаки , ». Корректируется запись на доске.

- Запишите с помощью нового знака предложения о том, что обезьяна, тигр и жираф принадлежат множеству Z. Выделяю для этого 30 секунд.

Ученики выполняют задание в тетради быстрее и убеждаются в том, что время на его выполнение значительно сократилось. Даже если это не так, учителю необходимо создать «иллюзию»:

- Ребята, вы выполнили задание за 20 секунд! Вы молодцы! Похлопайте себе. (…)

- Вам понравилось сегодняшнее путешествие?(…)

- Все ли персонажи, с которыми вы встретились, изображены у вас в тетради? (Нет Чебурашки.)

- Почему? (Чебурашка не принадлежит множеству Z.)

- Изобразите Чебурашку на вашей схеме и запишите это предложение.

Дети дорисовывают схему в тетрадях, записывают на математическом языке утверждение «Чебурашка не принадлежит множеству Z». Один из учеников демонстрирует правильный вариант на доске:

 

                                                                                                                                              

 

 

 

 

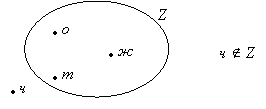
Путешествие в зоопарк заканчивается, но мы не прощаемся с его обитателями и обязательно встретимся с ними на уроках природоведения (окружающего мира).

Составление опорного конспекта.

А теперь сделайте запись для общего случая. Запишите под диктовку в рабочих тетрадях утверждения: «Элемент а принадлежит множеству А», «Элемент b не принадлежит множеству А».

Учащиеся работают самостоятельно. Учитель демонстрирует образец записи на доске, дети проверяют правильность своих записей. На доске:

 a  A

 b  A

Дополните опорный конспект схематическим изображением множества А и элементов а и b.

Один из учащихся работает на доске, остальные — в тетрадях:

 

 

 

 

- Сейчас, ребята вы получили новый эталон! МОЛОДЦЫ!

- Что вам теперь необходимо сделать? (Потренироваться.)

6. Первичное закрепление во внешней речи.

Цель:

зафиксировать в громкой речи способность к графическому изображению множеств и обозначению принадлежности элементов множеству знаками , .

Организация учебного процесса на этапе 6:

№ 5, стр. 11

- Откройте учебники на стр. 11 Выполним задание № 5.

Учащиеся выполняют задание с комментированием фронтально.

№ 4, стр. 11

- Следующий номер № 4 выполните, работая в парах.

Дети выполняют задание в парах, пользуясь опорным конспектом и комментируя его громкой речью. Если кто-то сидит один, то учитель слушает комментарий этого ребёнка. Проверка проводится фронтально.

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) тренировать способность к самоконтролю и самооценке;

2) проверить свое умение пользоваться знаками  и .

Организация учебного процесса на этапе7:

- Готовы проверить себя, как вы научились строить диаграммы Венна и пользоваться знаками , ;

- Что надо сделать, чтобы это проверить? (Выполнить самостоятельную работу.)

- Я предлагаю каждому из вас самостоятельно выполнить задания № 2, 3,
стр. 10. Успешной вам работы!

Учащиеся работают самостоятельно. На самостоятельную работу отводится 2–3 минуты.

- Закончили работу.

Учитель помещает на доску эталон для самопроверки.

- Проверьте себя по эталону и зафиксируйте результат проверки при помощи знаков «+» или «?».

Дети выполняют самопроверку и фиксируют ее результат.

- Какие возникли затруднения? (Перепутал знаки; забыл перечеркнуть знак «принадлежит»; не понял задание…)

- Скажите, в чем причина ошибок? (Не совсем понял тему; был невнимателен…)

- Исправьте ошибки по эталону.

- Поднимите руки те, кто сделал все верно. (…)

8. Включение в систему знаний и повторение.

Цель:

1) тренировать способности к схематическому изображению множеств с помощью диаграммы Венна;

2) начать подготовку учащихся к изучению темы «Пересечение множеств»;

3) тренировать навыки составления буквенных выражений по тексту задач на кратное и разностное сравнения.

Организация учебного процесса на этапе 8:

№ 7, стр. 11.

- С самостоятельной работой справились, теперь я вам предлагаю выполнить задание
№ 7 на стр. 11.

Учащиеся работают в тетрадях с печатной основой, проговаривая решение в громкой речи:

Построим диаграмму множества А. Для этого обведем девочек с мячом замкнутой линией.

Построим диаграмму множества В. Для этого обведем девочек с цветком замкнутой линией.

Психологическая трудность заключается в том, что вторая линия пересекает первую. Это им сделать трудно, поскольку они имели дело лишь с непересекающимися множествами.

Учитель может сам задавать вопросы из второй части задания:

- Сколько девочек принадлежат множеству А, но не принадлежат множеству В? (4.)

- Сколько девочек принадлежат множеству В, но не принадлежат множеству А? (3.)

- Сколько общих элементов у множеств А и В? (Одна девочка с мячом и цветком.)

- Кто может показать схему?

Желающий выходит к доске, появляется запись:

 

 

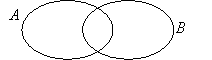
- Девочка с мячом и цветком находится как внутри диаграммы множества А, так и внутри диаграммы множества В. Как это изобразить?(…)

На доске в схеме учитель сам отмечает точкой общий элемент множеств A и B:

 

 

 

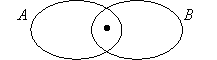
-Какой элемент находится в общей части множеств А и В? (Девочка с мячом и цветком).

- Молодцы! Вы настоящие первооткрыватели! Ученый Джон Венн гордился бы вами!

№ 9, стр. 12.

Данное задание выполняется устно. Дети считают по цепочке:

 37 · 2 = 74 62 · 10 = 620 58 : 2 = 29

 5 · 18 = 90 200 · 3 = 600 72 : 4 = 36

№ 10, стр. 12.

- А теперь выполните одно из любимых вами заданий — «Блиц-турнир». Работайте быстро и правильно!

Дети работают самостоятельно. Проверка выполняется фронтально с фиксацией на доске соответствующих выражений:

 а) а ∙ 2; б) b + (b + c); в) n –  k – k ∙ 3; г) (x + y) : 5.

9. Рефлексия учебной деятельности на уроке.

Цель:

1) зафиксировать новое содержание, изученное на уроке: построение диаграмм Венна, знаки , ;

2) зафиксировать неразрешенные затруднения, как направления будущей учебной деятельности;

3) оценить собственную деятельность и работу класса в целом;

4) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9:

- Что нового вы узнали на уроке.( …)

- Какую цель вы ставили перед собой сегодня? Достигли вы цели? Докажите.

- Когда у вас всех возникли затруднения на уроке? (Когда мы придумывали графическое изображение множеств, использовали знаки  и , решали задачи.)

- Как же графически обозначаются множества? (С помощью диаграммы Венна, замкнутой линией.)

- Что она показывает? (Элементы, расположенные внутри замкнутой линии, принадлежат множеству. Элементы, расположенные вне ее — не принадлежат.)

- Кто вам помог с этим разобраться? (Жители зоопарка.)

- Как вы теперь можете задавать множества? (Перечислением, графически, общими свойствами.)

- Кто считает, что он теперь принадлежит множеству ученых первооткрывателей?(…)

Дарю вам значок          

 

- А теперь оцените свою работу на уроке, возьмите свои треугольники.

- Спасибо за работу. Молодцы!

 

Домашнее задание:

записать опорный конспект;

 № 8, 11 (а), стр. 12;

☺ №  6, стр. 11 — по желанию.