Урок. "Дослідження функції за допомогою похідної та побудова графіків"
Тема: Дослідження функції за допомогою похідної та побудова графіків.
Мета: Узагальнити й систематизувати отримані раніше знання з цієї теми; сприяти формуванню у студенті логічного мислення шляхом залучення їх до аналізу теоретичного матеріалу й використання на практиці; удосконалити вміння будувати графіки; виховувати інтерес до вивчення математики, акуратність під час ведення записів і виконання побудов графіків функцій.
Тип уроку: узагальнення й систематизація знань.
Обладнання уроку: дошка, лінійка, підручник (Афанасьєва О.М.; Бродський Я.С. Математика 11 клас).
Епіграф уроку: «Недостатньо лише зрозуміти задачу, треба мати бажання розв’язати її. Де є бажання, знайдеться і шлях.» (Д. Пойа)
Очікувані результати:
- застосувати набуті знання до дослідження функції (за допомогою похідної) та будувати її графік;
- аналізувати власні помилки;
- працювати індивідуально і в групі;
- оцінювати свої знання і групи в цілому;
- розвивати пізнавальні інтереси учнів.
Структура уроку.
І. Організаційний момент.
ІІ. Мотивація навчальної діяльності.
ІІІ. Перевірка домашнього завдання та актуалізація опорних знань і вмінь.
IV. Робота з групами.
V. Підбиття підсумків уроку.
VІ. Домашнє завдання диференційованого характеру.
Хід уроку
І. Організаційний момент
ІІ. Мотивація навчальної діяльності.
Викладач. Уже досить тривалий час ми з вами вивчаємо похідну, і не тільки її красу з погляду математики, а й використання для розв’язання математичних задач. Ви вже досить термінів вивчили, щоб узятися за розв’язання більш складних задач, наприклад задач на побудову графіків функцій.
Отже, приступаємо. Сподіваюся, що потім ви з легкістю зможете впоратися з побудовою графіків будь-яких функцій, провівши їхнє дослідження.
ІІІ. Перевірка домашнього завдання та актуалізація опорних знань і вмінь.
Додому було дано графік функції ![]() . Цей графік вимагав від вас і дослідницьких зусиль. На дошці ви бачите деякі етапи дослідження функції при побудові цього графіка.
. Цей графік вимагав від вас і дослідницьких зусиль. На дошці ви бачите деякі етапи дослідження функції при побудові цього графіка.
Четверо студентів, які підуть до дошки, мають спробувати знайти помилку або неточність у дослідженні, зробити необхідні висновки або запропонувати більш раціональний підхід до дослідження функції ![]() .
.
У цей час інші студенти напишуть тестову роботу.
Тестове завдання
З наведених відповідей вибрати правильну.
1. Знайти D(),(х)=![]() .
.
А) (-∞;∞); В) [-3;3];
Б) (-3;3); Г) [-3;2)U(2;3].
2. Знайти нулі функції ![]() .
.
А) Функція нулів немає;
Б) -3; 3;
В) 3;
Г) -3.
3. Яка з даних функцій є непарною?
А) ![]() ; В)
; В)![]() ;
;
Б) ![]() ; Г)
; Г)![]() .
.
4. Знайти екстремуми функції ![]() .
.
А) 3; В) -3;
Б) 8; Г) -1.
5. Знайти вертикальні асимптоти графіка функції ![]() .
.
А) х=0, В) х=5; х=1;
Б) х=2; х=3; Г) х=0; х=2.
6. Знайти проміжки зростання функції ![]() .
.
А) (-∞; 4);
Б) (-∞;0)U(0; ∞);
В) (-4;5);
Г) (-∞;∞).
Відповіді до тесту
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Г |
Г |
А |
Г |
В |
Г |
Роботи двох-трьох студентів, які швидше за всіх упоралися з тестами, перевіряються викладачем. Після цього студенти міняються зошитами і перевіряють один-одного.
У цей час четверо студентів, викликані раніше до дошки, уже готові до відповідей.
На першій дошці.
1. ![]() .
.
1) D(у): ![]()
2) ![]() – функція ні парна, ні непарна.
– функція ні парна, ні непарна.
3) Точки перетину графіка з вісями координат:
Вісь Оу: х=0; у=1; А(0; 1);
Вісь Ох: у=0; ![]() , (x-1)(
, (x-1)(![]() +x-2)=0; x=1;
+x-2)=0; x=1; ![]() +x-2=0; x=-2; x=1
+x-2=0; x=-2; x=1
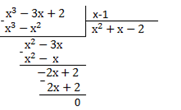
B(1;0); C(-2;0).
На другій дошці.
![]()
Висновок: у х=1 – розрив І роду;
Х=2 – вертикальна асимптота, тому що ![]() ∞;
∞; ![]() ∞;
∞;
Пошук асимптот: у=![]() – рівняння похилої асимптоти.
– рівняння похилої асимптоти.
![]()
![]()
Висновок: у=х+3 – похила асимптота.
На третій дошці
![]() D(
D(![]() ): х
): х![]()
![]()
![]()
у(0)=1; у(4)=9; стаціонарні точки
х=0, х=4.
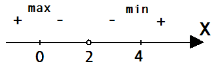
(На дошці не були спочатку розставлені знаки й не зазначені точки екстремуму й проміжки монотонності.)
На четвертій дошці
![]()
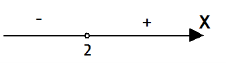
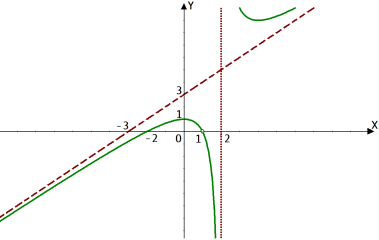
(На графіку не виколювати х=1, учні самі мають помітити помилку та виправити її.)
Підбиття підсумків роботи на цьому етапі: підрахувати кількість балів, отриману при тестуванні; відзначити роботу студентів біля дошки; підкреслити, що при дослідженні даної функції спрацювали всі пункти схеми дослідження.
IV. Робота з групами.
Створимо чотири однорідних за складом групи.
Розглядається графік функції ![]() .
.
І група. Знайдіть область визначення функції; дослідіть її на парність; знайдіть точки перетину графіка з осями координат.
1.D(y)= ) (-∞;0)U(0; ∞) – симетрична відносно початку координат.
2. y(-x)=![]() – функція загального вигляду.
– функція загального вигляду.
3. Точок перетину з віссю Оу: немає; з віссю Ох: немає.
ІІ група. Знайдіть асимптоти графіка функції.![]() ;
; ![]() . х=0 - вертикальна асимптота.
. х=0 - вертикальна асимптота.
2. Похила асимптота ![]()
![]() (за правилом Лопиталя).
(за правилом Лопиталя).
![]()
![]()
ІІІ група. Проведіть дослідження функції на монотонність і екстремуми.
![]() =
= ![]() ; D(
; D(![]() )=D(y);
)=D(y);
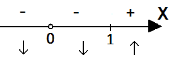
Функція спадає, якщо xє![]() .
.
Функція зростає, якщо xє[1;![]() ).
).
![]()
IV група. Проведіть дослідження опуклості функції.
![]()
D(![]() )=D(y).
)=D(y).
Після захисту біля дошки кожної групи, у всіх зошитах є дослідження розглянутої функції. Тепер всі групи будують графік даної функції.
Група, що впоралася із завданням першою, демонструє своє розв’язання біля дошки.
Основний принцип математичного аналізу, його ідеологія полягають у кінематичному підході до функції. Це означає, що акцент робиться на вивченні зміни функції залежно від зміни аргументу, її розвитку в часі. Можна сказати, що при побудові графіків функцій наше завдання – виходячи з локальних характеристик, одержати зображення в цілому. При цьому сам апарат нерідко грає допоміжну, уточнюючу роль, у той час як якісна картина може бути отримана й без нього.
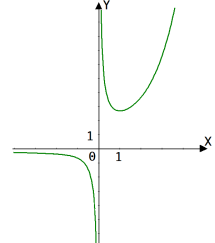
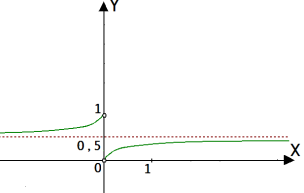
Звернімося до графіка ![]() .
.
![]()
Поміркуємо: якщо![]()
Якщо![]()
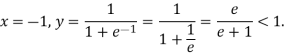
V. Підбиття підсумків уроку
1) Кожний студент заповнює листок самооцінки.
|
Прізвище______________________________ |
Кількість балів |
|
Тестування (по 2 бали за одне завдання) |
|
|
Відповіді біля дошки (максимум 12 балів) |
|
|
Участь у роботі групи (максимум 10 балів) |
|
|
Усього |
|
2) Запитання до класу
- Наскільки ти був готовий до уроку?
- Як ти працював у групі?
- Чи використовувалися раніше отримані знання і які?
- Чи цікавою була форма проведення уроку?
- Що корисного для себе ти одержав на цьому уроці?
VІ. Домашнє завдання диференційованого характеру.
Дослідіть функцію та побудуйте її графік.
-
y=
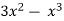 (середній рівень);
(середній рівень);
-
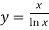 (достатній рівень);
(достатній рівень);
-
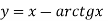 (високий рівень).
(високий рівень).


про публікацію авторської розробки
Додати розробку
