Урок. Застосування визначеного інтеграла до розв’язування прикладних задач

Тема: «Застосування визначеного інтеграла до розв’язування прикладних задач»

Мета: поглибити і розширити знання студентів про визначений інтеграл, продовжити формування навичок знаходити визначений інтеграл, показати його місце і значення в розв’язуванні задач геометричного та фізичного змісту. Сприяти розвитку творчих здібностей студентів, формувати їх пізнавальний досвід, вміння виступати перед аудиторією. Розвивати логічне мислення, інтелектуальні здібності студентів. Виховувати інтерес до науки , вміння раціонально використовувати робочий час.

Тип уроку: застосування знань, умінь та навичок.

Обладнання : мультимедійний проектор, комп’ютерні презентації студентів, таблиці.

Хід уроку

І. Організаційний момент

Розпочинаємо урок - телеміст, який проводимо між представниками різних творчих  та наукових кіл «науковцями» , «фізиками», «математиками- практиками» та «істориками».

ІІ. Мотивація навчальної діяльності, повідомлення теми й мети уроку

Тема сьогоднішнього уроку «Застосування визначеного інтеграла….». Мета уроку – поглибити знання з теми «Визначений інтеграл», показати його місце і значення  в розв’язуванні задач геометричного і фізичного змісту. І нехай девізом нашого уроку стануть такі слова «Будь-яка наука тільки тоді досягає досконалості, коли вона користується математикою».

ІІІ. Актуалізація й систематизація опорних знань , умінь та навичок

З метою безперервної роботи нашого телемосту проведемо перевірку             зв’язку. Підпишіть картку індивідуальних досягнень. Отже починаємо «Телерозминку» з теми «Первісна та інтеграл». Результати взаємоперевірки занотовуйте до карток ваших індивідуальних досягнень. Наш час обмежений, тому працюємо швидко й продуктивно.

1. Перевірка й повторення базових знань «Телерозминка».

Заповнити таблицю ( кожна правильна відповідь 0,5 б.).

Відповіді перевіряємо за допомогою мультимедійного проектора.

2. А зараз відповідаючи на запитання вікторини «Що? Де? Як? Чому?»,  ми налаштуємось на розгляд більш складних проблем.

Питання:

1. що таке первісна?
2. сформулювати основну властивість первісної;
3. чому дорівнює значення визначеного інтеграла на відрізку [a;b]?
4. Назвіть формулу Ньютона-Лейбніца.

Кожна відповідь оцінюється в 0,5 б.

3. Перевірка і поглиблення рівня засвоєння студентами знань і вмінь.

Розв’язування різнорівневих завдань за власним вибором. Знайти визначений інтеграл.

  І рівень (1 бал)

  II рівень (2 бали)

  III рівень (3 бали)

Перевірте правильність виконаних завдань и виставте бали у таблицю.

IV. Поглиблення і розширення  знань та їх застосування  

А зараз давайте з ясуємо як саме ми можемо застосувати визначений інтеграл у геометрії при знаходженні площ фігур; у фізиці в задачах на рух, на роботу на знаходження маси тіла.

Слово надаю творчій групі «Науковців».  (творча група підготувала           комп’ютерну презентацію). На кожну парту  викладається  напрацювання  цієї групи, а саме різні види і формули обчислення їх площ.

Зараз виконуємо завдання (працюємо в парах).

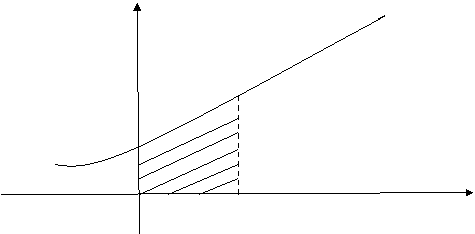
Серед наведених інтегралів виберіть ті,  за допомогою яких  можна обчислити площі криволінійних трапецій, що зображені  на рисунках.

Установіть відповідність між визначеним інтегралом і криволінійною трапецією.

1.             y                                                            a)                             

                                     б)

                                                                               в)

                                                                                г)

  0      1     2                                х               

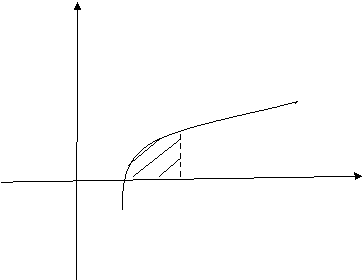
2)          y                                                                 д)

 є)

                                                y=lnx                        ж)                                                         

            0           1         2                        х

3) у

                                   y=            

                -1 0 1                                     

4)

                                         1

                                             0       1    2                                   x

Перевіряємо правильність виконання завдання на мультимедійному екрані і виставляємо бали у картку індивідуальних досягнень.

Слова надається групі «Фізики».

(Творча група підготувала презентацію)

Студенти записують формули для знаходження  шляху, роботи та маси тіла у зошит.

Слово надається групі «Математики-практики».

(Творча група підготувала комп’ютерну презентацію)

Розв’язки задач студенти записують у зошиті. А зараз розв’яжемо з вами  задачу на знаходження площі плоскої фігури біля дошки.

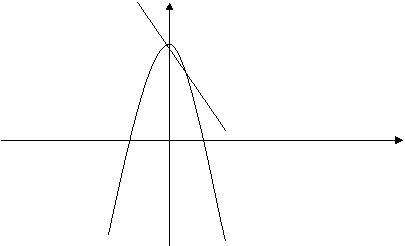Ст.149 №64(7)                                                         у

     4 

                                                              3

                                                                1

x    0    1                                         0                                            x

y    4     3

Ст.150 №16

F(x)=4 H,

x=2cм=0,02м

F(x)=kx- закон Гука (сила пропорційна розтягу або стискy)

x- величина розтягу або стискання

F(x)=200x.  Нехай t- довжина пружини, тоді

Відповідь: .

А зараз слово  надається творчій групі  «Історики». Студенти підготували        комп’ютерну презентацію по інтегральне  числення та про вчених І. Ньютона та Г. Лейбніца.

V. Підсумок уроку.

Підрахуємо бали в своїх картках індивідуальних досягнень.

Чи сподобався вам урок?

Чим самим сподобався?

Рівень засвоєних деяких питань уроку та вивченого раніше на потрібних перевіримо за допомогою кросворда.

Запитання до кросворда.

1. Першу букву якого слова  нагадує знак інтеграла? (Сума)
2. Хто з відомих математиків-фізиків дослідив  фізичний зміст інтеграла? (Ньютон)
3. Хто з відомих математиків дослідив геометричний зміст інтеграла? (Лейбніц)
4. Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла? (криволінійна)
5. Як називається функція, яка стоїть під знаком інтеграла? (підінтегральна)
6. Як називається множник dx у підінтегральному виразі? (диференціал)
7. Як називається операція обернена до операції диференціювання? (інтегрування)

VI. Домашнє завдання.

повт. п. 26 ст.136-138, ст. 144-145 №64 (6°, 8, 13*), №66 (1,2) ст.150.