Урок "Формули для обчислення довжини вектора,кута між векторами, що задані своїми координатами".

Розв'язання задач — зовсім не привілей                              

   математики. Усе людське пізнання — це

не що інше, як постійна постановка і

розв'язування все нових питань, проблем.

                                                                                               Е.Ільєнков

Тема заняття. Формули для обчислення довжини вектора,     кута між векторами, що задані своїми координатами. 

Вид заняття. Заняття узагальнення та систематизації знань, умінь,   навичок.

Мета заняття.

Навчальна. Узагальнити та систематизувати вміння  учнів з теми:”Вектори і координати в просторі”. Реалізувати  поняття скалярного добутку між векторами, довжини вектора, кута між векторами, що задані коордитнатами. Формувати вміння та навички учнів застосовувати вивчений матеріал до розв’язування задач.

Виховна.   Виховувати культуру мови  в ході бесіди, математичну культуру, навики самостійно приймати рішення; створювати передумови формування загальнолюдських вмінь та навиків учнів, формувати творчий та естетичний потенціал учнів.

Розвиваюча. Розвивати у учнів вміння практичної реалізації  системи знань в

                      систему вмінь.

Хід заняття

1.               Організаційна частина
2.               Перевірка домашнього завдання
3.               Підготовка до заняття. Оголошується тема,  мета та завдання заняття.

 

 Актуалізація опорних знань учнів.( фронтальна бесіда- бліц - опитування, математичний диктант )

Питання для фронтальної бесіди.

1. Що називається вектором?

             Очікувана відповідь: вектором називається напрямлений відрізок

2. Як позначається вектор?

              Очікувана відповідь: або однією малою латинською або двома   

               великими латинськими буквами з символом у вигляді вектора.

3. Що називається довжиною вектора?

              Очікувана відповідь: довжиною вектора є довжина відповідного

              йому відрізка.

4. Які вектори називаються рівними?

              Очікувана відповідь: рівним називаються вектори,  які мають

              однакові довжини і є співнапрямленими.

5. Що називається сумою векторів 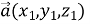і ()?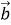

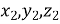            Очікувана відповідь:сумою векторів є вектор, кожна координата

            якого є сумою відповідних координат векторів   і

            ()

6. Що називається добутком вектора  на деяке число λ?

           Очікувана відповідь: добутком вектора  на число λ є

            вектор, кожна координата якого є добутком числа  λ на

              координати вектора

           

7. Який вектор називається нульовим?

             Очікувана відповідь: нульовим вектором називається вектор,

             початок і кінець якого співпадають, його довжина дорівнює нулю.

8. Які вектори називаються колінеарними?

              Очікувана відповідь: колінеарними називаються вектори, які

              лежать на одній прямій або паралельних прямих. Координати

              колінеарних векторів пропорційні.

9. Які вектори називаються компланарними?

             Очікувана відповідь: вектори називаються компланарними, якщо    

              вони належать одній площині.

10.  Що можна сказати про компланарність двох будь – яких  векторів?

            Очікувана відповідь: два вектори завжди є компланарними.

 

Математичний диктант.(метод - самоперевірка )

Дано вектори:

Варіант 1                                                  Варіант 2

 (3; 0; 4); (7; 0; 2);                           (2; -2; 0); (3; 0; -3).

Запишіть:

1) координати вектора , якщо = + , (2 бали)

2) координати вектора , якщо = 2 - ; (2 бали)

3) координати вектора , якщо відомо, що довжина вектора втри­чі більша довжини вектора ; (2 бали)

4) при якому значенні k вектор (k; 0; 6) колінеарний вектору ; (2 бали)

5) чи компланарні вектори , та (0; 0; 1)? (2 бали)

Відповідь.

Варіант 1.1) (10; 0; 6).  2) (-1; 0; 6). 3) (-9; 0; -12), (9; 0; 12). 4) k = 21.  5) Так.

 Варіант 2. 1) (5; -2; -3). 2) (1; -4; 3). 3) (6; -6; 0), (-6; 6; 0).

4) k = - 6.   5) Hi.

Вивчення нового матеріалу.(пояснення, розповідь, бесіда, ілюстрація, тренувальні вправи).

 

 Формула для обчислення довжини вектора. Приклади.

     На попередньому занятті ми з вами з’ясували, що довжиною вектора є довжина відповідного йому відрізка. Отже, якщо вектор визначено початком і кінцем в точках відповідно:  і , то довжиною вектора буде величина, що дорівнює:

                  (1)

Якщо ж координати вектора відомі: , то його довжина відповідно буде дорівнювати:

.                                                             (2)

Для закріплення нових формул пропоную наступні приклади:

№1. Дано точки  і . Знайти довжину вектора .

Розв’язування.

За формулою  (1): = =

=.

№2. Знайти довжину вектора .

Розв’язування.

За формулою (2): ==

№3. Знайти довжину вектора , якщо ; .

Розв’язування.

, тоді

№4. Знайдіть довжину діагоналі АС паралелограма ABCD, якщо А (2; - 6; 0),        В (-4; 8; 2), D (0;-12;0).

Розв'язування

Оскільки (- 6; 14; 2), (-2; -6; 0), то = + , AC (-8; 8; 2)

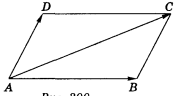(рис. 300).

Тоді = = = 2 (лін.  од. )

 

Скалярний добуток векторів. Приклади.

Скалярним добутком векторів ()  ) ∙ ()  назива­ється число (скаляр)

               · = .                               (3)      

№5. Знайдіть · , якщо (-2; 3; 1), (-4; -5; 2).

Розв’язування.

· =-2

№6. Дано вектори (2; -1; 4), (5; 3; n). При якому значенні п скаляр­ний добуток векторів дорівнює -3?

Розв’язування.

· =2;

10-3+4n=-3;

4n= -10;

 n= -2, 5

    Із означення скалярного добутку двох векторів і випливають його властивості:

1) · = · .

2) ( + ) · = · + · .

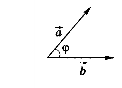
3) Скалярний добуток векторів і дорівнює добутку їх абсолютних величин на косинус кута між ними  (рис. 297):

                       · = · cos φ                                          (4)

 

Наслідки із властивості 3:

1)                                                 

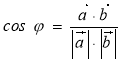
2) Два відмінні від нуля вектори і перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.

Кут між векторами, що задані своїми координатами. Умова ортогональності векторів. Приклади.

Як видно було із наслідка з властивості 3 скалярного добутку: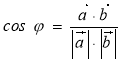

Якщо дану рівність записати у координатному вигляді, то:

                                                     (5)

№7. Знайдіть · , якщо = 5, = 4, а кут між векторами дорів­нює 120°.                          

 

№8. Чи перпендикулярні вектори (2; 3; 6) і (3; 2; -1)?

№9. При якому значенні m вектори (6; 0; 12) і (-8; 13; m) перпенди­кулярні?

Узагальнення та систематизація знань, умінь та навичок учнів

По горизонтали
2. Величини які крім числового значення мають ще й напрямок та точку прикладання  (векторні)
4. Якщо в результаті дії утворюється число то такі дії називають (скалярними)
9. Якщо два вектора лежать на одній прямій або на паралельних прямих то вони (колінеарні)
10. Якщо в результаті дії утворюється вектор то такі дії називають (векторними)
11. Якщо два вектора напрямлені в одному напрямку то вони (співнапрямлені)
12. Квадратна матриця в якої по діагоналі стоять відмінні від нуля числа, вище неї будь-які числа, а нижче - лише нулі (діагональна)
13. Матриця в якої кількість рядків дорівнює кількості стовпців (квадратна)
16. Частина алгебри, що вивчає вектори, векторні простори, лінійні відображення та системи лінійних рівнянь (лінійна)
17. Рівняння в якому змінні знаходяться у першому степені (лінійне)

По вертикали
1. Величини які для своєї характеристики використовують лише числові значення  (скалярні)
3. Діагональна матриця в якій по діагоналі стоять одиниці, а решта нулі  (одинична)
5. Три вектора які лежать в одній площині (компленарні)
6. Величина, яка характеризується числовим значенням і напрямком (вектор)
7. Довжина реального відрізка, що відмовідає заданому вектору (модуль)
8. Три некомпленарних вектора можуть утворювати ……. Базис  (просторовий)
14. Якщо рівнв довжини двох векторів то вони (рівні) 
15. Розділ математики, що вивчає математичні операції і відношеня, та утворення, що базуються на них: многочлени, алгебраїчні рівняння, алгебраїчні структури (алгебра)

 

Підведення підсумків заняття.

    Викладач підводить підсумки заняття,  відмічає роботу студентів, коментує отримані бали на занятті.

 Домашнє завдання.

1.Скласти кросворд  до теми  ”Координати та вектори” (для всіх бажаючих покращити оцінку за тему).

2. Виконати вправи:

№1. Дано точки А (1; 0; - 2), В (-2; 1; 3) і вектор (1; 0; - 2) . Знайдіть:

а) координати вектора

б) абсолютну величину вектора

в) координати суми векторів і .