Урок "Формули коренів квадратного рівняння"

Добропільський міський відділ освіти Добропільської міської ради

Добропільська загальноосвітня школа І - ІІІ ступенів №19

Добропілької міської ради Донецької області

 

 

 

 

 

План – конспект

  уроку алгебри в 8 класі з теми:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вчитель

математики та

інформатики

вищої категорії

Стешенко Марина

Анатоліївна

2017 рік

Мета:

Навчальна

 

• познайомити учнів з основними формулами знаходження коренів повного квадратного рівняння;
• познайомити з правилами оформлення розв’язку квадратного рівняння;
• формувати вміння знаходити корені квадратного рівняння, використовуючи  його означення та формули;
• домогтися засвоєння формул коренів квадратного рівняння.

 

Розвиваюча

 

• розвивати обчислювальні  навички, уміння аналізувати  й узагальнювати;
•  розвивати інтерес до математики.

Виховна

 

• виховувати  позитивне ставлення до навчання, почуття відповідальності, активність, культуру емоцій, точність, акуратність.

 

Задачі уроку:  познайомити учнів з поняттям дискримінанту, вивести формулу коренів квадратного рівняння, учити застосовувати її при розв’язуванні квадратних рівнянь.

 

Тип уроку: засвоєння нових знань та вмінь.

 

Обладнання уроку: комп’ютери, проектор, роздавальний матеріал, зошит, підручник, довідники.

 

 

 

 

 

 

 

 

 

 

 

 

                Якщо ти почуєш, що хтось не полюбляє математику -  не вір.

Її  не можна не любити  –  її можна тільки не знати.

 

Хід уроку

І. Органійзаційний етап.

- Добрий день, шановні діти та гості, які присутні на нашому уроці. Сьогодні  урок ми проведемо за схемою, яка розташована на моєму блозі й представлена у вигляді інтерактивного плакату Glogster.

Сценка. (До класу заходить учень, який сильно хромає).

- Що трапилось?

- Я бігав по коридору та впав. Здається, що вивихнув ногу.

- Чим же ми можемо тобі допомогти?

- Ви ж займаєтеся алгеброю? Значить, ви і зможете мені допомогти.

- Дивно! Хоча ... (слайд Сценка)

Повідомлення учня. Термін "алгебра", як назву мистецтва відновлення, у арабів перейшов і в медицину. Мистецтво лікаря "костоправа" так само називали алгеброю, а самого лікаря – алгебраїстом.

Вчитель: Це все вірно, але ми тобі допомогти нічим не зможемо. Ми вивчаємо алгебру, квадратні рівняння. Алгебра від слова "аль - джебр" - відновлення, заповнення або "перенесення доданків з однієї частини рівняння в іншу". Вибач, тобі необхідно звернутись до лікаря.

ІІ. Перевірка домашнього завдання, актуалізація опорних знань.

1. Перевірка домашнього завдання за заздалегідь записаними відповідями на дошці.
2. Фронтальне опитування (слайд Актуалізація )

?  Які рівняння ви бачите на екрані? /Квадратні/

 ? Доведіть, що дані рівняння квадратні.

? Перелічіть види квадратних рівнянь, які зображені на екрані. /Неповні квадратні рівняння, повні квадратні рівняння, зведені квадратні рівняння).

? Які методи ви застосовуєте при розв’язанні  квадратних рівнянь?

/1. При роз’вязку  неповних  квадратних рівнянь треба застосувати означення квадратного кореня (коли немає доданку при х), або винесенням х за дужки; 2. Виділити повний квадрат).

3. Математичний диктант (слайд Математичний диктант )

Варіант 1	Варіант 2
Запишіть квадратне рівняння. Підкресліть однією лінією старший коефіцієнт, двома лініями – другий, трьома – вільний член.
а) б) 13х - 5 в) 12 +  г)	а) б) 11 - 2 в) 14 -  г)
2) Складіть квадратне рівняння  a, у якому:
а)  a=1,     b= -2,   c= 3; б)  b= 4,   a=-1,     c= 4; в)  c= -5;   a=2,      b= -1; г)  b= 0,    c= 9;      a=-1	а)  a=2,     b= -1,   c= 5; б)  b= -5,   c= 3;     a= - 1; в)  c= -4;  b= 2;       a= -3; г)  с= 0,    а= 5;     b = - 3
3)Виділіть квадрат двочлена:
а) 4; б)	а) 9; б)

 

ІІІ. Вивчення нового матеріалу

1.               Мотивація (слайд Мотивація, звернення учнів 5 класу за поміччю у розв’язку задачі)

• Шановні учні 8 класу. При підготовці до олімпіади з математики, ми розв’язували задачу  на складання рівняння, але наших знань не вистачає, щоб отримати відповідь, допоможіть нам.

Життєва задача: Фермер виділив під баклажани ділянку прямокутної форми розмірами 8 × 10 м. Для захисту від шкідливих комах він висадив базилік уздовж двох сусідніх сторін ділянки, як показано на малюнку. Визначте ширину смуги, зайнятої базиліком, якщо загальна площа, зайнята базиліком і баклажанами, становить87,36 м² .

Розв’язання

Якщо позначити ширину смуги, яку виділено під базилік,через х м, то сторони прямокутника, що містить і баклажани,і базилік, дорівнюватимуть (8+x) м і  (10+ x) м. Оскільки загальна площа ділянки становить 87,36 м²  , то складемо рівняння:

(8+х)⋅ (10+х ) = 87,36 .

(Один учень виходить до дошки й починає розв’язувати рівняння інші записують у зошити)

(8+х)⋅ (10+х ) = 87,36 ;

80+8х+10х+х²=87,36;

х²+18х+17,36=0

• Отже, розв’язання задачі зводиться до розв’язання рівняння, що відрізняється від неповних квадратних рівнянь та й спосіб виділення квадрата двочлена у повному квадратному рівнянні тут не ефективний. Треба застосувати інший спосіб розв’язку повного квадратного рівняння.

? Яку мету ми перед собою поставимо на цьому уроці? (Спробувати знайти інший спосіб розв’язку  квадратних рівнянь)

- Запишемо тему урока «Формули коренів квадратного рівняння»

 

2.               Відкриття нових знань.

 

• Історія алгебри поглиблюється своїми коренями в давні часи. Задачі,які пов’язані  з рівняннями розв’язувались ще у Древньому Єгипті та Вавілоні. Теорія рівнянь цікавила та цікавить математиків усіх часів та народів. У Древній Індії були поширені публичні змагання по розв’язку  важких задач. Ввиведення формули коренів квадратного рівняння в загальному вигляді є у Вієта, але він признавав тільки додатні корені. Італійськиі  математики 16 ст. визнають додатні та від’ємні числа. Тільки в 17 ст.завдяки працям Ньютона, Декарта та інших вчених спосіб розв’язку  квадратних рівнянь приймає сучасний вигляд. Над проблемою розв’язку   квадратних рівнянь математики бились на протязі декількох століть.
• Сьогодні ви легко навчитись розв’язувати любе квадратне рівняння, на заздрість математикам Древньої Греції та Індії.
• Щоб кожного разу не проводити великі обчислення, нам досить одного разу розв’язати  рівняння в загальному вигляді та отримати готові формули для коренів квадратного рівняння.

(Вчитель виводить формули на дошці, учні записують у довідники з математики)

ах²+ bx +c = 0

 

- Спробуємо встановити, як зв’язані  корені квадратного рівняння  з числами а, b, с.  Числа а, b, с ми бачимо в квадратному рівнянні, а коренів – ні. Будемо шукати корені.

-  Спочатку виділимо в рівнянні повний квадрат. Для цього розділимо рівняння на старший коефіцієнт а.

x² + +   = 0

•  Отримали формулу квадрата суммы: спочатку додамо, а потім віднімемо вираз .

 

.

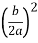Перетворимо отримане рівняння:

= 0

В лівій частині запишемо квадрат суми, а в праву  перенесемо все інше.

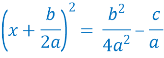
 Спростимо праву частину: з одного дробу віднімемо інший.

.

Зверніть увагу на знаменник в правій частині.

? Від’ємне чи додатнє це число? /Знаменник цього дробу завжди додатній/.

Тобто, тільки від чисельника, який стоїть в правій частині злежить, скільки коренів має це квадратне рівняння. Тому такий чисельник й має  в математиці власне ім’я. Його називають дискримінантом квадратного рівняння й позначають буквою D.

.

•                   В математиці досить  рідко буває, щоб введений термін не мав життєвого підгрунтя.
•                   Згадайте слово «дискримінація». Що воно означає?/Воно означає приниження одних і піднесення інших, тобто різне відношення до різних людей/
•                   Обидва ці слова ( дискримінант,  дискримінація) походять від латинського discriminans – який розрізняє.
•                   Дискримінант розрізняє квадратні рівняння по кількості коренів. В залежності від  значення дискримінанту квадратне рівняння може мати один чи два кореня, а може не мита коренів зовсім. Роздивимось кожний з цих випадків.

, D < 0.

• Якщо дискримінант менше від нуля, то квадратне рівняння коренів не має.

, D = 0,

           

           

      x = .

- Якщо дискримінант дорівнює нулю, то квадратне рівняння має тільки один корінь.

 

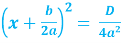3. , D > 0.

• Якщо дискримінант більше за нуль, то квадратне рівняння має рівно два різних дійсних кореня. Отримати їх можна за готовою формулою. А отримані при цьому формули ми й будемо використовувати в подальшому для знаходження коренів.

, 

,   

x = ,

  x =.

  – формула коренів квадратного рівняння  (слайд Опорний конспект)

 

 

ІV. Засвоєння нових знань і вмінь

 

1. Первинне закріплення

 

Складемо блок-схему розвязку квадратних рівнянь

? При розв’язанні повного квадратного рівняння, що в першу чергу обчислюється?/Дискримінант/

? Якщо треба скласти програму для обчислення квадратного рівняння, то яку команду використовували? /Команду розгалуження/

• Давайте складемо блок-схему для обчислення квадратного рівняння.

? Які дані вхидні?

? Які дані вихідні?

? Які дані не ввійшли до вхідних та вихідних даних? Чому?

/На дошці будується блок-схема програми/

? В яких програмах можна скласти програму обчислення коренів квадратного рівняння? /Паскаль, Ексель/

 

2. Робота за підручником

 

          № 1 Розв’язати  рівняння:

                                               3х² + 8х – 11 = 0.

                                             a = 3, b = 8, c = – 11

D = b² – 4ac = 8² – 4 · 3 · (–11) = 64 + 132 = 196, D > 0

Ответ. 1; –3.

           № 2. Розв’язати  рівняння:

– 9х²+6х – 1 = 0.

 Як показує досвід зручніше мати справу з квадратними рівняннями, у яких старший коефіцієнт додатній. Тому спочатку помножимо обидві частини рівняння на  (–1), отримаємо:

9х²– 6х + 1 = 0

D = 0, x = .

x =

           № 3. Розв’язати  рівняння:

2х² – х + 3,5 = 0.

                   D = – 27,  D < 0.

       Рівняння  коренів не має.

 

4)Робота з класом

 

№ 4 х² – 5х + 6 = 0,  D = 1, x₁ = 2, x₂ = 3;

№ 5 х² – 2х – 15 = 0,  D = 64, x₁ = –3, x₂ = 5.

 

  5)Виконання завдань на картках із друкованою основою

 

- Два учні за комп’ютером в програмах Паскаль та Ексель запрограмують розв’язок повного квадратного рівняння, всі інші розв’язують в зошитах рівняння, а в таблицю вносять дані, потім перевіряють виконання на комп’ютері.

 

Завдання: Заповнити таблицю, де a, b, c – коефіцієнти квадратного рівняння виду ах²+ bx +c = 0, D – його дискримінант, х₁ і х₂  - корені.

 

Варіант 1

Рівняння	a	b	c	D	х1	х2
х2 + 42х + 441 = 0
х2 + 8х + 7 = 0
3х2 -13х + 14 = 0

 

Варіант2

 

Рівняння	a	b	c	D	х1	х2
х2 – 34х + 289 = 0
х2 + 4х – 5 = 0
2х2 – 9х + 10 = 0

 

 

V. Підбиття підсумків уроку

 

1) Яку мету ми поставили перед собою на цім уроці?

2) Чому вона виникла?

3) Чи досягли  ми своєї мети?

 - Діти, прочитайте прислів'я  "Математика - гімнастика розуму".

? Що таке гімнастика?

Вислухавши відповіді, вчитель підводить підсумок:

Гімнастика - це система вправ для фізичного розвитку людини; гімнаст - людина спритна, стрункий, сильний, пластичний, гарний.

Математика також багато дає для розумового розвитку людини - змушує думати, міркувати, шукати прості і красиві рішення, допомагає розвивати логічне мислення, вміння правильно і послідовно міркувати, тренує пам'ять, увагу, загартовує характер.

 

VІ. Домашнє завдання

 

Самою важкою й  важливою справою для кожного учня є виконання домашнього завдання. Якщо домашнє завдання виконано правильно, то на уроці ви відчуваєте себе набагато впевненіше.

§21 – читати, вивчити означення, алгоритм розв’язку рівнянь,  № 813, № 815

Додаткове завдання: При яких додатних значеннях m обидва корені рівняння 0,25х²+7х+m=0 рівні між собою?