Урок "Гармонічні коливання"

Розробка інтегрованного з фізики та математики 

Клас: 10

Тема уроку: Гармонічні коливання

Мета уроку:

1. ввести поняття гармонічних коливань;
2. продовжити формувати уміння виконувати перетворення графіків тригонометричних функцій;
3. вивчити фізичний зміст величин ,що входять в рівняння гармонічних коливань;
4.  навчити учнів складати рівняння, будувати і аналізувати графіки гармонічних коливань;
5.  продовжити формувати уміння виконувати перетворення графіків тригонометричних функцій;
6. показати міжпредметний зв’язок і сприяти усвідомленню єдності наук фізики та математики;

7) розвивати пізнавальну активність учнів, пам’ять, увагу та уяву, логічне мислення, уміння аналізувати, порівнювати;

8) виховувати свідоме і відповідальне ставлення до навчання, поглиблювати інтерес до вивчення математики і фізики, формувати атмосферу співпраці на уроці.

Тип уроку: інтегрований урок .

 Методи: розповідь, бесіда, пояснення , демонстрація,  ілюстрація, виконання вправ.

Наочність , обладнання:  Комп’ютер, інтерактивні моделі маятників, «LearningApps.org.» і «Physics Animations/Simulations»

Хід уроку

І. Організаційна частина

Привітання класу.

ІІ. Постановка цілей уроку.

Мобілізація уваги учнів. Вступне слово вчителя.

Доброго дня шановні учні ,кожному добре відомі явища ,що чергуються і знову повторюються.: ранок ,день ,вечір , нічь і знову ранок ,день…; зима , весна , літо ,осінь і знову зима, весна ,літо…По фізичним  законам  і маятник годинника повторює свій рух і наше серце ,поршні у двигуні автомобіля ,і струна гітари , землетрус-повторення руху ,повторює своє значення і змінний струм ,Земля повторює свій рух навколо Сонця і навколо своєї осі .

 Всім відомо -фізика і математика упродовж століть крокують поряд, доповнюючи і пояснюючи одна одну.  Як писав Рене Декарт: «Той, хто серйозно прямує до пізнання істини ,не повинен займатись якоюсь однією наукою ,бо всі вони тісно пов’язані між собою» . Сьогодні під час уроку я пропоную вам встановити зв’язок між тригонометричними функціями і законами руху ,що повторюється з часом. Описати і вивчити фізичні процеси математичними поняттями.

ІІІ. Актуалізація опорних знань.

Для успішного засвоєння теми уроку перевіряємо, як виконано домашнє завдання і повторимо деякі властивості тригонометричних функцій та побудову графіків ф-цій за допомогою геометричних перетворень відомого графіка функції .Будуємо графік функції у=-2sin(2х-п/4)за допомогою графічного калькулятора https://www.mathway.com/ru/Graph і порівнюємо з отриманим при виконанні домашнього завдання

І проводимо фронтальну бесіду:

-Які тригонометричні ф-ції  вам відомі?

-Що є графіком ф-ції у=sinx, y=cosx?

-Які властивості має ф-ція  y=sinx,y=cosx?

-Який найменший додатний період має ф-ція y=sinx ; y=cosx?

-Які перетворення ми використовували  для того ,щоб побудувати заданий графік  функції у=-2sin(2х-п/4).

V.Сприймання та усвідомлення нового матеріалу.

 Тема нашого уроку «Гармонічні коливання»

 Відео https://sz076.sharepoint.com/:v:/s/7-589/EYn9MiPMSPRCoRYavOCXVCkBBi_foWJobeuRVWZd82xN_A?e=RKbewK

1)Механічні  коливання -це рух,який повторюється через певний інтервал часу.

2) В математиці змінюються періодично функції синуса, косинуса, тангенса і  котангенса

То які ж функції можуть описати коливальний рух ?Порівняємо коливання груза на пружині і побудову графіка у=sinx

1. побудова графіка функції у=sinx https://aziza2017.ucoz.net/postroenie_sinusoidiy.gif
2. Коливання пружинного маятника https://www.vascak.cz/data/android/physicsatschool/templateimg.php?s=kv_harmonicke_kmitani&l=en

Висновок : Зміну координати тіла, можуть описувати функції y=sin x,y = cos x і дійсно, цими функціями можна описати будь-який коливальний рух.

Періодичні зміни фізичної величини в залежності від часу, які відбуваються за законом синуса або косинуса називаються гармонічними коливаннями. Рівняння гармонічних коливань: y = A sin (ωt+α) , y = A cos (ωt+α)

На екрані відео:https://sz076.sharepoint.com/:v:/s/7-589/EfdYBr2SYmJBipR-jXyTV-8BWPpy3j_xpxvdpdV4BJGY_g?e=ql8z8i

Основні характеристики гармонічних коливань

А – амплітуда коливань; характеризує найбільше відхилення точки, що коливається від положення рівноваги

ωt +  α – фаза коливань, яка визначає стан коливальної системи у будь-який момент часу (рад)

ω – кутова швидкість (рад/c)

α – початкова фаза коливань

t – час (с)

Т= 2π/ ω – період коливань (с) – це час, за який точка здійснює одне повне коливання

V  = 1/T = ω/2π – частота коливань, вона показує, скільки коливань точка здійснює за 1 с.

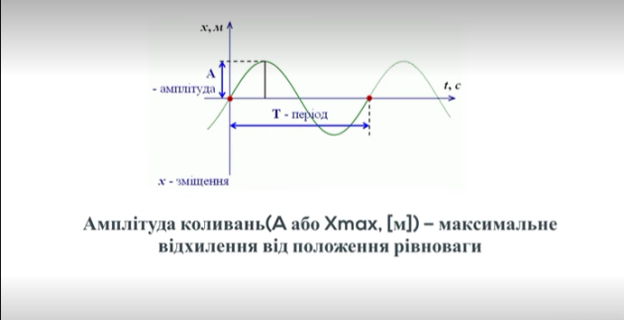
Подивіться на малюнок ,який є  на дошці і скажіть що є незалежною змінною і функцією гармонічних коливань?( відповідь t- аргумент або  незалежна змінна ;x-функція)

Тому формально  можна змінити позначки на осі абсцис з х на t а у на х Використовуючи графік цієї функції цієї функції  знайдемо амплітуду ,період і частоту .

VI.  Формування вмінь.

Вправа 1 . Учні за допомогою вчителя розв’язують задачу:

Координата  тіла, що рухається, змінюється за законом   х(t) = 4 cos(5 π t + π/3)(СМ). Знайдіть амплітуду, період, частоту коливання. Обчисліть координату тіла в момент  часу t = 2 c.

      Розв’язання:

1)А=5 – амплітуда;

2)Т= 2π/ω; T = 2π/5π= 2/5=0,4 (c);

3) V = 1/T=5/2=2,5 1/с

4) зміщення-X(t) = x(2) = 4 cos(3π*2+π/3) = 4 cos (6π+π/3) = 4cos(π/3)=4*1/2=2 см

 Вправа 2  Точка Р виконує гармонічні коливання вздовж відрізка АВ=16см. Відхилення L точки Р від середини відрізка АВ змінюється залежно від часу за законом:

     L = 8sin(