Урок геометрії в 11 класі "Надзвичайна ситуація "

Урок геометрії в 11 класі « Надзвичайна ситуація»

 

Мета: поглибити й розширити знання учнів із тем «Об'єми та площі поверхонь геометричних тіл»; формувати навички застосування знань до розв'язування прикладних задач; знайо­мити з поняттям надзвичайної ситуації, причинами виникнення та способами усунення наслідків надзвичайних ситуацій.

Тип уроку:  удосконалення знань та вмінь

 

І. Актуалізація опорних знань

 

1

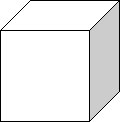
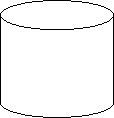
                                                                     Що спільне і відмінне в даних фігур?

 

                                                                        Як обчислити поверхню та об`єм?

 

 

 

 

 

 

 

 

 

 

 

 

2.Записати формулу для обчислення(учні виконують на картках):

1. Довжини кола;
2. Площі рівностороннього трикутника
3. Радіуса описаного кола навколо трикутника
4. Площі паралелограма
5. Радіуса вписаного кола в квадрат
6. Площі довільного трикутника
7. Площі круга
8. Радіуса описаного кола навколо прямокутного трикутника

3.Усні задачі

Задача 1 Основа призми та діагональний переріз 4-кутної призми – квадрат. Сторона основи 4 см . Знайти бічну поверхню та об`єм призми.

 

Задача 2 Осьовий переріз циліндра – квадрат, площа якого 36 см². Знайти бічну поверхню та об`єм циліндра.

 

Задача 3 Сторона основи правильної трикутної піраміди 3 см. Висота піраміди – 2 см. Знайти бічну поверхню та об`єм піраміди.

Задача 4 Осьовий переріз конуса – рівносторонній трикутник, периметр якого – 12 см. Знайти бічну поверхню та об`єм конуса.

 

Вступне слово вчителя

Сьогодні тама надзвичайних ситуацій особ­ливо актуальна у світі, зокрема в Україні.

Що називають надзвичайними ситуаціями  і які чин­ники, спричиняють їх виникнення?              

Надзвичайна ситуації - це порушення нор­мальних умов життя та діяльності людини,на об`єкті або  території; викликане аварією, ката­строфою стихійним  лихом або небезпечною ді­яльністю, що призводить до загибелі людей або значних матеріальних збитків. Природні ката­строфи трапляються внаслідок стихійних явищ  природи,техногенні  - унаслідок людської діяльності,  зокрема в результаті непрофесіоналізму, службової недбалості, безвідповідальності , байдужості. Будь – яка надзвичайна ситуація вимагає

проведення  рятувальних, медичних, інженерних та інших робіт щодо усунення її наслідків.

Давайте спробуємо уявити, що кожна наша група є групою спеціалістів математиків-інженерів, яка виїхала на об'єкт, де сталося сти­хійне лихо  для того щоб виконати розрахунки для ліквідації наслідків

 

 

ПЕРШИЙ ТУР «ПРИКЛАДНА ЗАДАЧА»

 Група І

Землетрус — це природна катастрофа, підзем­ні поштовхи в земній корі, які спричиняють коливання земної поверхні, її деформацію, руйнування інженерних споруд.

Задача

Водонапірна башта, яка мала форму прямокутного циліндра була зруйнована під час землетру­су. Скільки необхідно цегли на її відбудову, якщо висота башти 12 м, радіус -  3 м, товщина стінок має дорівнювати 0,12 м, а виміри однієї цеглини — 6 см х 12 см х 24 см?

Група 2

Ураган -  це вітер величезної руйнівної сили та чималої тривалості. Причиною виник­нення ураганів є різке порушення рівноваги в атмосфері. Ураганний вітер руйнує міцні і зносить легкі споруди , спустошує посіви, валить стовпи ліній електропередач_,  пошко­джує транспортні магістралі й мости, призводить до людських жертв.

 

Задача            

 Ураган зруйнував  дах будівлі , що має форму правильної чотирикутної піраміди , сторона осно­ви якої дорівнює 8м,висота - 3 м; Скільки листів цинку необхідно придбати, щоб відновити дах, якщо розміри одного листа 1 м х 2 м?

Група З

Повінь – затоплення території внаслідок виходу із русел великих та малих річок. Повені призводять до затоплення будинків, руйнування гідротехнічних споруд, дамб, шляхів мостів. Усі повені обмежують господарську діяльність на охоплених ними територіях, блокують роботу транспорту, знищують результати сільськогосподарських робіт.

Задача

Під час повені підвал багатоповерхівки зато­пило водою. Яку частину доби необхідно витра­тити, щоб відкачати воду, якщо висота підвалу становить Зм, довжина — 20 м, ширина — 10 м, а потужність насосу — 100 м³ / год?

 

Група 4

Пожежа — це неконтрольоване горіння поза спе­ціальним вогнищем. Лісова пожежа — некероване горіння лісу, що знищує дерева й кущі, заготовлений ліс, будівлі. Унаслідок пожежі зменшуються захисні, водоохоронні та інші корисні властивості лісу, знищується цінна фауна, порушується планове ведення лісового господарства та використання лісових ресурсів. Боротьба з лісовими пожежами вимагає надлюдських зусиль, великих коштів, а іноді супроводжується й людськими жертвами.

Задача

Унаслідок пожежі вигоріла ділянка лісу, що має форму паралелограма, діагоналі якого дорів­нюють 300 м і 150 м, а кут між ними 30°. Скіль­ки потрібно саджанців, щоб відновити ліс, якщо деревця розсаджують на відстані 50 см одне від одного та 3 м між рядами.

 

ДРУГИЙ ТУР «КОНСУЛЬТАЦІЯ»

 

Учні на планшетах записують відповіді на запитання, які ставить учитель, звертаючись до кожного по черзі. Кожен учень має відповісти на шість запитань.

 

1.  Як називається чотирикутник, протилежні сторони якого паралельні?

2.  Як називається відрізок, що сполучає проти­лежні вершини чотирикутника?

3.  Запишіть формулу для обчислення площі паралелограма, діагоналі якого дорівнюють d1 і d2, а кут між ними дорівнює  φ.

4.  Зобразіть фігуру, площа якої обчислюється за формулою S = ab

5.  Чому дорівнює sin 30°?

6.  Що вимірюють, коли користуються одини­цями 1а, 1 га, 1 км²?

7.  Запишіть у гектарах   3 790 000 м².

8.  Яку величину обчислюють за формулою C=2πR?

9.  Обчисліть довжину кола, якщо його радіус дорівнює 3 мм.

10.  Як називається пряму призму, осно­вою якого є прямокутник?

11.  Зобразіть геометричну фігуру, яка є гранню прямокутного паралелепіпеда.

12.  Скільки лінійних вимірів має прямокутний  паралелепіпед?

13.  Запишіть формулу для обчислення об'єм? прямокутного паралелепіпеда.

14.  Чому дорівнює периметр квадрата зі стороною а?

15.  Чому дорівнює площа прямокутника зі сто роками 4 дм і 3 см?

16.  Яку величину вимірюють, коли користуються одиницями 1 мм³, 1 см³, 1 дм³, 1 м³?  

17.  Обчисліть об'єм прямокутного паралелепіпеда, якщо його виміри дорівнюють

      3 мм 5 мм, 6 мм.

18.  Зобразіть фігуру, яка є бічною гранню піраміди

19.  Як називається висота бічної грані правильної піраміди, проведена з вершини

     піраміди

20.  Запишіть формулу для обчислення площі  бічної поверхні правильної піраміди.

21.  Обчисліть площу бічної поверхні правильне піраміди, периметр основи якої

       дорівнює 21 см, а апофема — 4 см.

22.  Яке геометричне тіло утворюється в результаті обертання прямокутника навколо

       однієї з його сторін?

23.  Запишіть формулу для обчислення площі бічної поверхні циліндра.

24.  Обчисліть площу бічної поверхні циліндра радіус якого дорівнює 2 м,

         а висота — 5 м.

 

ТРЕТІЙ ТУР «РОЗВ'ЯЗУВАННЯ ПРИКЛАДНИХ ЗАДАЧ»

 

Керівник кожної групи біля дошки представляє розв'язання задачі, одержаної від іншої групи. Учасники гри, у разі необхідності, ставлять йому питання, на які може відповідати керівник або будь-який інший член групи, що розв'язувала задачу, про яку йдеться.

Задача 1

Водонапірна башта, яка мала форму прям* го циліндра, була зруйнована під час землетрусу. Скільки необхідно цегли на її відбудов; якщо висота башти 12 м, радіус — 3 м, товщина стінок має дорівнювати 0,12 м, а виміри одні цеглини — 6 см х 12 см х 24 см?

 

Розв'язання.

Обчислимо площу бічної поверхні циліндра за формулою S = 2πRH.

                         S = 2-3,143.12 = 226,08 м².

Оскільки товщина стінок башти збігається виміром цеглини, що дорівнює 12 см, знайдемо  площу бічної грані цеглини, утвореної сторонами 6 см і 24 см.

                        S = 0,060,24 = 0,0144 м².

Тоді кількість цеглин дорівнює:

                     226,08:0,0144 = 15 700 штук.                   Відповідь. 15 700 штук.

Задача 2

Ураган зруйнував дах будівлі, що мав форму правильної чотирикутної піраміди, сторона осно­ви якої дорівнює 8 м, а висота — 3 м. Скільки листів цинку необхідно придбати, щоб відновити дах, якщо розміри одного листа 1м х 2 м?

 

Розв'язання.

Площу бічної поверхні піраміди обчислимо за формулою S= p*l,

                                        де p— півпериметр основи піраміди, І — апофе­ма.

                  S = 16*5 = 80 м².

Площа одного листа цинку дорівнює 1*2 = 2 м².

 Тоді кількість листів цинку дорівнює: 80:2 = 40 штук.

                                                                                Відповідь. 40 штук.

Задача З

Під час повені підвал багатоповерхівки зато­пило водою. Яку частину доби необхідно витра­тити, щоб відкачати воду, якщо висота підвалу становить 3 м, довжина — 20 м, ширина — 10 м, а потужність насосу — 100 м³ / год?

Розв'язання.

 Обчислимо об'єм підвалу за формулою V=abc.

                           V = 3*20*10 = 600 м³.

Враховуючи потужність насосу, знаходимо час, необхідний для відкачки води:

600:100 = 6 год =- доби.

                                                                      Відповідь. 1/4 доби.

 

 

Задача 4

Унаслідок пожежі вигоріла ділянка лісу* що має форму паралелограма, діагоналі якого дорів­нюють 300 м і 150 м, а кут між ними 30°. Скіль­ки потрібно саджанців, щоб відновити ліс, якщо деревця розсаджують на відстані 50 см одне від одного та 3 м між рядами?

Розв'язання,

 Обчислимо площу паралелогра­ма за формулою S =1/2 d_1* d_2*sinφ:

                              S = ½ *300*150*sin30° = 11250 м².

Враховуючи, що на одному квадратному метрі росте два саджанці, знаходимо кількість са­джанців, необхідну для відновлення лісу:

1125*2 = 22 500 штук.

                                         Відповідь. 22 500 саджанців.

Підсумок уроку

«Так» чи «ні»

1. Чи сподобався урок?

2. Чи актуальні питання розглядалися на уроці?

3. Чи мали труднощі у розв`язуванні задач прикладного характеру?

4. Чи переконала у необхідності вміння знаходити об`єм та площу поверхні геометричних тіл.

 

Домашнє завдання:Скласти прикладні задачі на знаходження об`єму та площі поверхонь геометричних тіл.