Урок-семінар по темі "Піраміда"

Тема уроку: Урок-семінар по темі: «Піраміда»

Мета уроку: узагальнити, систематизувати знання, вміння й навички   учнів з даної теми;

 розвивати просторову уяву та логічне мислення.
Обладнання: мультимедійний проектор, моделі пірамід, таблиці.

Девіз уроку: Без ентузіазму ніякої математики.

І. Перевірка домашнього завдання.

За малюнками, заготовленими на перерві на дошці,

2 учні пояснюють розв’язання задач № Н З Н А

(І рівень) і № 452а(ІІІ рівень) в такому порядку:
а) додаткові побудови;

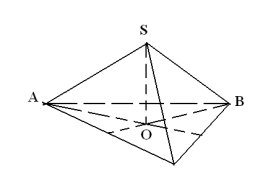б) формула для знаходження об’єму піраміди та площі бічної поверхні;
в) обчислення площі основи і висоти піраміди.
№ 434а:  І рівень
  

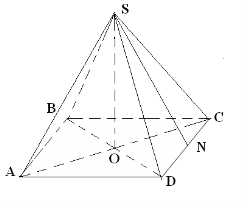
ABCD-правильна піраміда

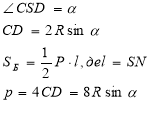
SND=90°)SN=R sin

S

2. Діти, сьогодні в нас урок-семінар «Розв’язування задач по темі “ПІРАМІДА”.

          На урок ви повторили не тільки теоретичний матеріал, що стосується даної  теми,  але й повинні навести приклади, де в повсякденному житті ми зустрічаємось із пірамідами. В другій частині півпари ви напишете диференційовану самостійну роботу.

ІІІ. Актуалізація опорних знань учнів

 1.Що таке піраміда ?

 2.Що таке висота піраміди ?

 3.З чого складається поверхня піраміди ?

 4.Що таке ребра піраміди, бічні грані ?

 5.Яка піраміда називається правильною ?

 6. Що таке вісь правильної піраміди ?

 7.Поясніть, що таке зрізана піраміда ?

 8. Наведіть формули, за допомогою яких можна обчислити площу бічної поверхні та об’єм піраміди.

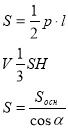
V=)

9. В якому випадку площу бічної поверхні піраміди знаходимо за формулою S=

III. Усне розв’язування задач (малюнки до задач – на мультимедійній дошці).

1. В основі піраміди лежить прямокутник, сторони якого 6см і 8см. Всі бічні ребра дорівнюють 13см. Обчисліть об’єм.

Розв’язання:

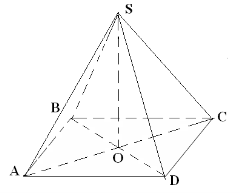S=24cм

Оскільки SA=SB=SC=SD, то АО=ВО=СО=ДО, як проекції рівних похилих.

Тому точка О-центр кола, описаного навколо прямокутника.

ОС=  SO=12см.  V=

2. В основі піраміди лежить рівнобедрений трикутник. Кожна бічна грань нахилена до площини основи під кутом 60˚. Знайти S

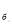
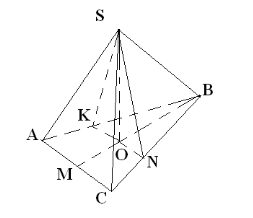Розв’язання
Прямокутні трикутники SMO, SKO, SNO рівні за спільними катетом SO і гострими кутами. 3 рівності  трикутників випливає, що MO=KO=NO, тобто O-центр кола, описаного навколо трикутника ABC.

 

Ми розв’язали дві задачі.

- В що проектується вершина піраміди, якщо всі бічні ребра рівні?

- В що проектується вершина піраміди , якщо всі двогранні кути при основі рівні?

IV .Письмове розв’язання задачі з коментуванням (із ДПА).(Виконують два учні: перший  - малюнок  і записує пояснення , другий - розв’язок)

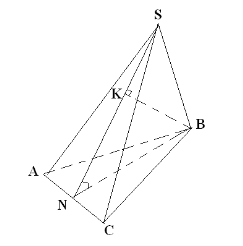SАВС- піраміда АВ=ВС ,

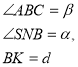
Розв’язання

З

З

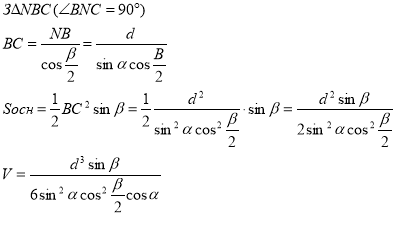
- Ми розв’язали задачу і ще раз переконались, де лежить висота піраміди, якщо дві грані перпендикулярні до площини основи.

- Де буде лежати основа перпендикуляра, проведеного  з основи висоти піраміди до третьої бічної грані ?

- А зараз наведіть приклади, де в повсякденному житті ми зустрічаємось з пірамідами.

 (Учні зачитуються цікаві спостереження).

- Йдучи дорогою, ми, інколи, милуємось плотом, бетонні стовпчики якого виготовлені у вигляді пірамід, любимо милуватися красивими дашками кіосків, грибочків на пляжі і не звертаємо увагу, що всі вони мають форму пірамід.

II. Усне розв’язування задач.

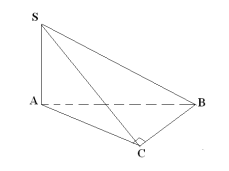1. Дано піраміду, в основі якої лежить прямокутний трикутник. Дві грані перпендикулярні до площини основи (які містять гострий кут), а третя нахилена під кутом Показати цей кут. (Малюнок на мультимедійній дошці.)

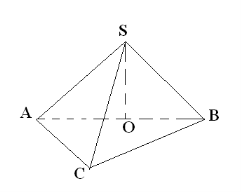2. В основі піраміди лежить рівнобедрений трикутник.  Грань, що містить бічну сторону, перпендикулярна до площини основи, а дві інші нахилені під кутом . Показати ці кути.

(Учні обґрунтовують кути нахилу граней і виконують малюнок в зошитах).

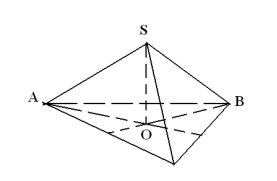3. У правильному тетраедрі ребро дорівнює а. Знайти площу повної поверхні тетраедра.

Порівняти два терміни (чи однакові твердження):

«правильна трикутна піраміда» і «правильний тетраедр».

Чи можна стверджувати, що вони означають одне й  те саме?

4. «Мені необхідно склеїти з картону модель піраміди, у якої в основі лежить ромб з кутом 60°, а всі бічні ребра, рівні між собою»,- сказав учень А.

«Такої піраміди існувати  не може»,- заперечив учень В. Чи правильне твердження учня В?

 V. Підсумок уроку. Виставлення оцінок. Домашнє завдання .

 VI. Виконання самостійної роботи із завдань ДПА.

  I.група: № 425(а, в)

  II.група: № 487(а, в)

  III. група: №453(а, в)

Самостійні роботи учні здають для перевірки.