Урок геометрії в 8 класі "Трапеція. Види та властивості трапецій"

Урок геометрії в 8 класі

Тема. Трапеція. Види та властивості трапецій

Мета уроку:

•       доповнити знання учнів властивостями та ознаками окремих видів трапецій і домогтися засвоєння змісту вивчених тверджень; сформувати вміння відтворювати вивчені властивості та ознаки окремих видів трапецій, а також використовувати їх у здійсненні послідовних міркувань під час розв’язування задач;
•       навчити застосовувати набуті знання та вміння до розв’язування задач;
•       розвивати логічне мислення, комунікативні математичні здібності;
•       виховувати культуру виконання побудов та записів у зошитах.

Тип уроку:  урок застосування знань

Обладнання: таблиця «Трапеція. Види та властивості трапецій», малюнок до прикладної задачі

ХІД УРОКУ

І. Організаційний момент

Геометрія – правителька всіх розумових пошуків.
М.В. Ломоносов

ІІ. Мотивація, формулювання мети і завдань уроку

        З метою створення позитивної мотивації навчальної діяльності учнів та формування розуміння логіки вивчення матеріалу можна звер­нутися до схеми, складеної на уроці № 10.

За цією схемою пропонуємо учням, користуючись раніше набути­ми знаннями, відповісти на запитання.

1.   Яку додаткову умову треба знати, щоб стверджувати, що поданий чотирикутник є паралелограмом?
2.   Чи правильно, що будь-який чотирикутник є паралелограмом?
3.   Чи є паралелограмом чотирикутник, тільки дві протилежні сторони якого паралельні? Виконайте зображення такого чотирикутника. Відповідаючи на запитання, учні мають дійти усвідомлення того факту, що:
   •       паралелограми (вивчені на попередніх уроках) є лише одним із при­наймні двох видів опуклих чотирикутників;
   •       окрім паралелограмів (які мають дві пари паралельних сторін), існу­ють чотирикутники, у яких лише одна пара паралельних сторін.

Таким чином, виділяється  геометричний об'єкт.

Дійсно сьогодні на уроці ми будемо розширювати знання про трапецію, розглядати її властивості, види — основна мета уроку.

Приклади застосування трапеції в побуті:

•       в интер’єрах (дивани,  підвісні стелі) (слайд 1);
•       в ландшафтному дизайні (слайд 2);
•       в індустрії моди (слайд 3);
•       в дизайні  предметів повсякденного використання (слайд 4);
•       в архітектурі.

ІІІ. Актуалізація опорних знань

1.   Бліц-опитування (кожному ряду задаю 2 запитання)

1.   Чи можуть довжини основ трапеції бути рівними?
2.   Чи може основа трапеції дорівнювати бічній стороні?
3.   Чи можуть бути рівними кути трапеції, що прилеглі до бічної сторони?
4.   Чи існує трапеція, у якої три кути гострі?
5.   Чи може сума кутів при більшій основі трапеції бути більшою за суму кутів при меншій основі?
6.   Яка трапеція має рівні діагоналі?

Отже, ми повторили властивості трапеції, які зібрані в узагальнюючій таблиці. Нею ми будемо користуватися при розв’язуванні задач.

2.               Усне розв’язування задач за готовими малюнками
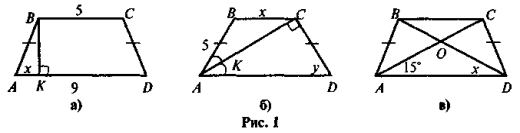
   1.                                        Чи правильно виконано рисунок 3?

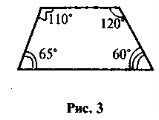
2.                                        На рисунку 4 AD || ВС. Доведіть, що 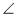С + 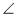D = 180°.

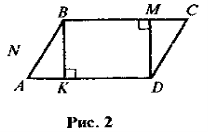
       3)   Знайдіть на рисунку 1 трапеції. Назвіть їх основи й бічні сторони.

3.   “Розумом атака”
   Розв'язують усно задачі, картки з умовами яких прикріплені на магнітній дошці (по варіантам).
   Задача 1. Один з кутів рівнобічної трапеції в 3 рази більший від другого. Знайдіть кути трапеції.
   (45°, 135°)
   Задача 2. Сума двох кутів рівнобічної трапеції дорівнює 120°. Знайдіть кути трапеції.
   (60°, 120°)

ІV. Оголошення, представлення теми та очікуваних результатів 

Робота з таблицею

1.   висота прямокутної трапеції дорівнює одній з її бічних сторін;
2.   діагоналі рівнобічної трапеції рівні, і навпаки, якщо діагоналі трапеції рівні, то вона рівнобічна;
3.   сума протилежних кутів рівнобічної трапеції дорівнює 180°;
4.   діагоналі рівнобічної трапеції утворюють з її основою рівні кути, і навпаки, якщо діагоналі трапеції утворюють з її основою рівні кути, то трапеція рівнобічна;
5.   висота рівнобічної трапеції, що проведена з вершини тупого
   кута, ділить більшу з основ на відрізки, один з яких дорівнює
   півсумі основ, а другий — піврізниці основ.

VI. Формування   умінь розв’язувати задачі

1.   У рівнобедреній трапеції висота, проведена з вершини тупого кута, ділить більшу основу на відрізки завдовжки 6 см і ЗО см. Знайдіть меншу основу трапеції.
2.   Знайдіть невідомі кути прямокутної трапеції, найбільший кут якої утричі більший за найменший.

VIІ. Застосування теоретичних знань в життєвих ситуаціях

1. Короткі історичні відомості презентує учень.

2. Сучасна Александрія простяглася на 25 км піщаною косою. З боку моря прикриває її скелястий острів Фарос. На цьому острові знаходилось одне із семи чудес світу – Александрійський чи Фароський маяк. Маяк мав в основі куб, а на ньому підставку, яка в перерізі являє собою трапецію. Зверніть увагу на рисунок–схему: трапеція – рівнобічна, верхня основа якої – 180 м, а бічна сторона – 100 м, кут нахилу бічної строни до нижньої основи дорівнює 60⁰. давайте знайдемо довжину нижньої основи.

VIIІ. Підсумки уроку

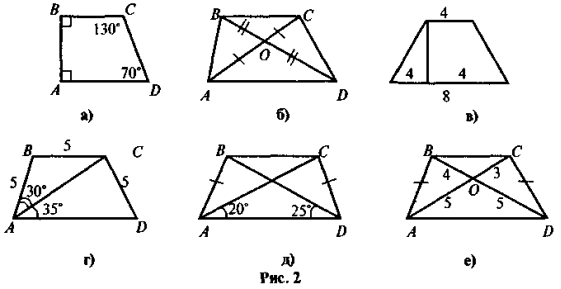
Якої помилки припустилися в зображенні трапеції на рис. 2?

VIII. Домашнє завдання

Вивчити зміст означень, теорем та їх доведення. Розв'язати задачі.

1.   Знайдіть кути прямокутної трапеції, якщо відношення найбільшого і найменшого з них дорівнює 3 : 2.
2.   Діагональ рівнобедреної трапеції є бісектрисою її тупого кута. Знай­діть периметр трапеції, якщо її основи дорівнюють 5 см і 10 см.
3.   Повторити властивість катета, що лежить проти кута 30°.