Урок-гра з алгебри для учнів 7 класу на тему "Використання формул квадрата двочлена та різниці квадратів у розв'язуванні вправ"

Використання формул квадрата двочлена та різниці квадратів у розв’язуванні вправ.

Урок-гра у 7 класі

Мета: формувати вміння і навички учнів застосовувати формули квадрата двочлена і різниці квадратів під час виконання тотожних перетворень виразів; виховувати увагу, спостережливість під час виконання завдання; формувати обчислювальні навички в процесі розв’язування різних типів завдань; розширювати кругозір учнів, пов’язуючи математику з іншими предметами.

Тип уроку: застосування вмінь та навичок.

Обладнання: картка походу, роздавальний матеріал, індивідуальні дошки, індивідуальні та колективні завдання, таблиця-підказка.

Хід уроку

 

I. Організаційний етап

II. Мотивація навчальної діяльності

Урок ми присвятимо закріпленню знань про формули скороченого множення.

Що ви чекаєте від сьогоднішнього уроку?

(«Мікрофон». Кожний з учнів може висловити свою думку, свої побажання щодо проведення уроку. Цей метод дає можливість визначити вчителеві напрям роботи на уроці, на що звернути увагу).

— У школу на адресу учнів 7 класу надійшла посилка. Подивіться, що в ній. (Посилку бере вчитель, відкриває.)

У коробці містяться всі ті завдання, які будуть розв'язуватись на уроці. Зверху лежить лист. Учитель його зачитує.

Шановні учні 7 класу, до вас звертається група альпіністів. Запрошуємо вас здійснити разом з нами сходження на вершину гори. Але гора незвичайна. Щоб нею піднятися, потрібно подолати багато перешкод, а вони будуть з'являтися у вигляді математичних завдань. Ми впевнені, що у вас вистачить терпіння, знань, навичок і вмінь і ви допоможете нам у цій нелегкій справі. Запевняємо, що ви не пошкодуєте. На вас чекає сюрприз.

З повагою, група альпіністів.

Ну що, не відмовляємось?

III. Розв'язування вправ

У кожного з вас є конверт, в якому знаходиться схема сходження (рис. 1) і фішка, за допомогою якої ви будете позначати своє місце знаходження. Якщо завдання виконано правильно, пересувайте фішку на 1 крок уперед, якщо неправильно, — повертайте назад. Перемагає той, хто першим досягне вершини.

Розпочинаємо з рівнини. Я вважаю, що перед сходженням вам потрібно розім'ятися. Працюємо з індивідуальними дошками. (У кожного учня є індивідуальна дошка, на якій він крейдою записує відповідь до поставленого завдання, піднімаючи, показує вчителю. Вчитель перевіряє правильність виконання і дає (чи не дає) згоди підійматися далі по «схилах гори».)

Завдання 1.

Піднесіть до квадрата вирази: 5а; -13kс; -0,3а; 2ху; -5а³b⁴;  х²y; - 11/12y³z²; 1,2x³y

Завдання 2.

Який одночлен піднесли до квадрата і дістати вирази: 1/9z⁴k⁶; 256a⁶b²; 0,16x²y²?

Завдання 3.

Знайдіть подвоєні добутки двох виразів: 4a i 1/2b; 7x i 5y; 1/4a i 4b; 3c i 1/9d; 2a i 6b.

Учитель. Завжди в дорозі легше йти, якщо това­риш поруч. Тож завдання наступне виконуємо в па­рах: в індивідуальних конвертах є по чотири завдан­ня: якщо їх розв'язати правильно, то отримаємо відповіді з конверта сусіда по парті, і сусід анало­гічно.

Завдання 4.

Подайте у вигляді многочлена вираз:

a)(3a + 10b)2; (9a2 + 60ab + 100b2)	a)(y4 + y3)2; (y8 + 2y7 + y6)
б)(1/2x – 4y)2; (1/4x2 – 4xy + 16y2)	б)(0,8a + 3b)2; (0,64a2 + 4,8ab + 9b2)
в)(7 – y3)2; (49 – 14y + y6)	в)(5 – x3)2; (25 – 10x3+ x6)
г)(10a – 9b)2; (100a2 – 180ab + 81b2)	г)(7x3y2 + 2xy)2; (49x6y4 + 28x4y3 + 4x2y2)
д)(ab – 1)2; (a 2b2 – 2ab + 1)	д)(mn - 2)2; (m2n2 – 4mn + 4)
e)(x4 – x2)2; (x4 – 2x6 + x4)	e)(0,1a – 10b)2; (0,01a2 + 2ab + 100b2)

 

Учитель. Сходячи по схилах гори, ми замовкаємо, щоб своїм гомоном не зрушити лавину снігу. Тож наступне випробування називається «Мовчанка».

Завдання 5.

Знайдіть неправильну відповідь. Я вам показую завдання і можливі до них відповіді. Ви мовчки підраховуєте (усно), підіймаєте сигнальну картку відповідного кольору. Зелена — правильно, червона — неправильно. Хто відповість правильно, переходить до наступного пункту.

(10x + 0,5y)² = 100x² + 10xy + 0,25y²;

9y² + c²d² + 6cd = (3y + cd)²;

p⁴ – 16 = (p² – 4)(p² + 4).

Учитель. Ми дійшли до перевалу.Відпочиваючи, зіграємо в настільну гру «Лото». Вам дано полотно лото із заповненими п'ятьма клітинками й картки із номером на одному боці та із завданням на другому. Я дістаю з мішечка кульку під певним номером, а ваше завдання — відшукати на полотні лото відповідь до завдання під цим номером і накрити його цією карткою.

Завдання 6.

Заповніть клітинки  «Лото».

 

x10 – 6x5b + 9b2		(n2  + 1)2	a2 – 14a + 49
	25y2 + 10y + 1	16m2 + 49n2 – 5mn

Полотна картки лото пронумеровані, під номерами карток різні завдання. Відповіді вчителю відомі наперед, щоб можна було швидко перевірити правильність виконання.

Учитель. Одного разу в англійському королівстві Камберленд знялася буря, сильний вітер виривав дерева з корінням, утворюючи вирви. В одній із таких вирв жителі виявили якусь чорну речовину. Назва цієї речовини графіт. Шматками графіту чабани стали мітити овець, купці робили написи на ящиках та кошиках. А що ви знаєте про графіт? (Розповідь учнів).

Учень 1. На уроках фізики ми вивчали різні стани речовини: твердий, рідкий, газоподібний. Графіт належить до твердих тіл. Тверді тіла поділяються на кристалічні та аморфні. Графіт – кристалічне тіло, має кристалічну решітку. Решітка графіту ніби поділена на шари, які легко зсовуються. Коли ми пишемо олівцем, то зсунуті нами кусочки графіту лягають у вигляді ліній на аркуші паперу.

Учень 2. На уроках географії ми вивчали, що графіт належить до метаморфічних порід.

Метаморфізм – це зміна гірських порід на великих глибинах під дією високого тиску та температури. Вапняк перетворюється в мармур, пісок – у кварц, граніт – у гнейс, вугілля – у графіт. Графіт є цінним мінеральним ресурсом, який широко використовується у виробництві фарб, темного скла, підшипників. В Україні залягають поклади графіту світового значення. Родовища графіту приурочені до порід Українського щита. Найбільші поклади цієї мінеральної мінеральної сировини в Кропивницькій області.

Учитель. Перед вами зображення кристалічної решітки графіту (рис.2). У ній чітко виражені шари розташування молекул. У кожному шарі молекули своїм розташуванням утворюють шестикутники. Ваше завдання — склас­ти ці шестикутники. Оскільки ми 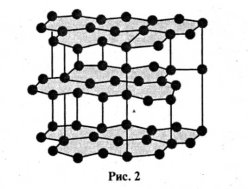розглядаємо три шари, то й клас розподілимо на три групи і кожна група отримує по шість завдань. Але кожен член групи виконує всі завдання. Хто першим правильно упорається із завданням (перевіряє вчитель), допо­магає іншим членам групи. Залежно від кількості виконаного завдання, учні отримують бали, додаю­чи до попередніх.

Завдання кожної групи написане на дошці. Лідер
групи йде його виконувати. 

Завдання 7.Складіть кристалічну решітку.

       Завдання для першої групи.

1.   Поставте замість зірочки вираз, щоб утворилася правильна рівність:

(* + 2b)² = a² + 4ab + 4b²;

(3x + *)² = 9x² + 6ax + a²;

(* - 2m)² = 100 – 40m + 40m².

2.  Виконайте множення:

(b – 2)(b + 2)(b² + 4).

3.Подайте у вигляді квадрата двочлена:

1/4x² + 3x +9.

1. Знайдіть значення виразу 98 ∙ 102, застосувавши формулу скороченого множення.

Завдання для другої групи.

1. Поставте замість зірочок вираз, щоб утворилась правильна рівність:

(3 + *)² = * + * + 49y²;

(15y - *)² = 225y² + 12x³y + 0,16x⁶;

(* + 2)² = * - 12ab + *.

2. Знайдіть значення виразу 6,01 ∙ 5,99.

3. Виконайте множення:

3. – y)(3 + y)(9 + y²).

4.Подайте у вигляді квадрата двочлена:

49x² + 64y² + 112xy.

Завдання для третьої групи.

1. Поставте замість зірочки вираз, щоб утворилася правильна рівність:

(2a + *)(2a - *) = 4a² – b²;

(* - b⁴)(b⁴ + *)= 121a¹⁰ – b⁸;

25a² – b⁶ = (* - b³)(b³ + *).

2.Подайте у вигляді квадрата двочлена:

100b² + 9c² + 60bc.

3.Знайдіть значення виразу, застосувавши формулу скороченого множення:

a) 74∙ 66;

б)199².

Учитель. От і дійшли ми до вершини знань. Учні, які проходили шлях невпевнено, отримують гребінці, щоб «причесати» свій розум,; учні, які пройшли половину шляху, отримують кульки, щоб піднятися до вершини знань: учні, які дійшли до вершини знань. Отримують шоколад, щоб відчути насолоду від перемоги.

Бали учні отримують залежно від свого розташування на схемі підйому.

ІV. Підбиття підсумків уроку.

V. Домашнє завдання.