ТЕМА УРОКУ

Кут між мимобіжними прямими. Кут між прямою і площиною. Кут між площинами

МЕТА УРОКУ

Дидактична:

• розглянути основні види кутів у просторі: кут між мимобіжними прямими; кут між прямою і площиною; кут між площинами;
• впевнитися в широкому застосуванні даних видів кутів в багатьох галузях життєдіяльності людини;

Розвиваюча:

• розвивати аналітичне мислення;

•      розвивати просторову уяву. Виховна:
•      виховувати графічну культуру студентів.

 

ТИП УРОКУ

Урок комбінований.

ПЛАН УРОКУ

1. Організаційна частина.
2. Перевірка домашнього завдання. Актуалізація опорних знань.
3. Повідомлення теми уроку. Мотивація.
4. Повідомлення нового матеріалу.
5. Закріплення матеріалу.
6. Підсумки. Домашнє завдання.

ХІД УРОКУ

 

I. Вітаюся. Відмічаю відсутніх.

II. Фронтальне опитування:

1) Яким може бути взаємне розташування прямих у просторі?

Прямі у просторі можуть перетинатися, бути паралель ними або мимобіжними.

2) Які прямі називаються мимобіжними?

Мимобіжними називаються прямі, які не лежать в одній площині і не перетинаються.

3) Як можуть бути розташовані у просторі пряма та площина?

Пряма може  належати  площині,   бути   їй  паралельною  або перетинати дану площину.

4) Якщо пряма перетинає площину, то скільки спільних точок вони
мають? Чому?

Якщо пряма перетинає площину, то вона має з нею одну спільну точку. Тому що за теоремою 1.2, якщо дві точки прямої належать площині, то і вся пряма належить даній площині

5) Яке взаємне розташування двох площин у просторі?

Дві площини у просторі можуть бути паралельними або перетинатися.

6) По якій фігурі перетинаються дві площини?

Площини перетинаються по прямій, що випливає з аксіоми стереометрії С_2.

 

III. Отже, основні фігури у просторі можуть не перетинатися, перетинатися або бути паралельними. Якщо вони паралельні, то що ми можемо сказати за кут між цими фігурами?

(Кут між фігурами буде дорівнювати нулю)

А яким чином знаходиться кут між даними фігурами у випадку коли вони перетинаються, ми з'ясуємо на даному уроці.

Тема уроку: "Кут між мимобіжними прямими. Кут між прямою і площиною. Кут між площинами." (Записують у зошити дату та тему уроку).

 

IV. Який вид кутів утворюють дві прямі, що перетинаються? (Вертикальні кути).

Так. Кутова міра меншого з них називається кутом між прямими.

Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні даним мимобіжним прямим. Цей кут не залежить від вибору прямих, що перетинаються.

Кутом між прямою та площиною називається кут між цією прямою і її проекцією на площину. Проекцією прямої на площину називається пряма, яка складається з основ перпендикулярів, опущених з точок прямої на дану площину.

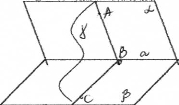Кутом між двома площинами називається кут між прямими перетину даних площин третьою площиною, перпендикулярною до лінії перетину даних площин.

 

- кут між та

 

 

 

Під час пояснення нового матеріалу я намагаюсь переконувати вас, що всі знання дуже потрібні, просто необхідні, у практичній діяльності людини. Щоб іще раз переконатись, що "Джерело і мета математики - в практиці", послухаємо доповіді. (Студенти роблять доповіді про практичне застосування кутів у просторі).

1. В будівництві.

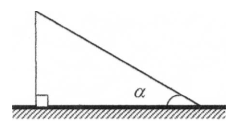
При  будівництві участків  доріг,  гребель,  каналів,  похилих дахів користуються кутом поперечного та поздовжнього схилу. Тобто на мал. 1

СFD - кут схилу і (1:3  або 33 ⁰ ). Маємо приклад кута між площинами, причому для встановлення лінії горизонталі часто використовують нівелір.

 

 

 

 

 

 

 

Мал.1

Відомі також кути природного схилу сипучих матеріалів: бурта картоплі - 45°, вугілля - 42°, ґрунту - 40°, глини - 30°, піску - 25-35°.

При зварюванні металу також не байдуже під яким кутом тримати електрод, а під яким - газовий пальник до поверхні металу. Електрод обов'язково тримати під кутом 45° до поверхні зварювання, бо в разі збільшення кута шлаки і шкідливі домішки будуть потрапляти в зону зварювання, що дасть неякісний шов зварювання. При меншому куті буде поганий провар металу і спостерігатиметься його розбризкування.

 2. В управлінні автошляхів.

При проектуванні і будівництві автомобільних доріг вираховують так званий кут перелому повздовжнього профілю дороги (мал.2). Він зумовлює видимість зустрічних авто і часто профіль змушено округлюють, знімаючи верх стрімкого горба, щоб уникнути аварійно небезпечних ділянок траси. Маємо приклад використання кута між півплощинами.

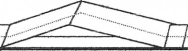
Мал. 2

3. В Укрзалізниці.

У точках спряження паралельних колій і на поворотах кут укосу створюють спеціально, щоб зрівноважити відцентровану силу (мал.З). Для цього зовнішню рейку піднімають над внутрішньою - міліметр підйому на кожний метр шляху (але не більше h=125 мм сумарно, тобто кут укосу буде обраховуватись так: ; ).

 

Мал.З     

4. В аеропорту.

Кути між мимобіжними прямими враховують при прокладанні повітряних трас для літаків; кут між прямою та площиною - при зльоті і посадці літаків. Пожежний літак приземляється на воду тільки під строго визначеним кутом, оскільки при його перевищені буде сильний удар об воду і можливий вибух.

5. В геодезії.

У геодезії і картографії, маркшейдерській справі(підземні прохідники) -усім править знання про кути. На мал.4 ви бачите екліметр - пристрій для вимірювання величини кута нахилу прямої до горизонту. ОР - нитка з вантажем, яка показує на шкалі величину шуканого кута РОВ.

 

 

 

 

 

 

 

 

 

 

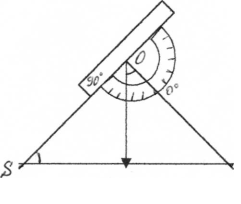
Знання про кути і Декартові координати допомагає встановити напрям прокладання тунелю в скелі, напрям підземних комунікацій (напрям лінії метро) у місті. Адже треба врахувати всі вже існуючі кабелі, труби, допустимі відстані до них. Знаючи початкові і кінцеві координати нового об'єкта вираховують кут його прокладання.

IV. Застосуємо отримані знання для розв'язування задач. №37 '

Відрізок завдовжки 10 м перетинає площину; кінці його знаходяться на відстанях 2 м і 3 м від площини. Знайдіть кут між даним відрізком і площиною.

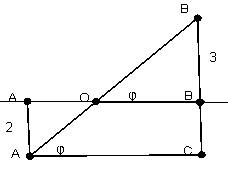
Дано: АВ - відрізок, ,

АВ=10 м, АА₁=2 м, ВВ₁=3 м,

 Знайти:

 

 

 

Розв'язання

1. Д/п АС ║ А₁В₁ (теорема 2.1)
2. ВОВ₁=ВАС = 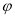(як відповідні)
3.                                                                                                                                                   Розглянемо АВС: С = 90° ВС=ВВ₁+В₁С=3+2=5 м

 

 

Відповідь: кут між відрізком і площиною дорівнює 30⁰ .

№38

З точки, яка віддалена від площини а на відстань а, проведено дві похилі, які утворюють з площиною кути 45° і 30°, а між собою - прямий кут. Знайдіть відстань між кінцями похилих.

 

Дано: , АD= а, BD i CD - похилі,

, ,

Знайти: ВС

Розв'язання

 

1) Розглянемо : а = 90°

2) Розглянемо : а = 90°

 

 

3) Розглянемо : D = 90°

За теоремою Піфагора ВС² = DВ^г + DС² = 2а² + 4а² = 6а²                   ВС=

Відповідь: відстань між кінцями похилих .

№43  (Усно)

Дві площини перетинаються під кутом 30°. Точка А, яка лежить в одній із цих площин, віддалена від другої площини на відстань а. Знайдіть відстань від цієї точки до прямої перетину площин.

№45

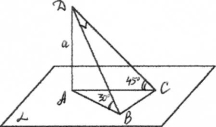
Два рівнобедрені трикутники мають спільну основу, а їх площини утворюють кут 60°. Спільна основа дорівнює 16 м; бічна сторона одного трикутника 17 м, а бічні сторони другого перпендикулярні. Знайдіть відстань між вершинами трикутників.

 

Дано: , - рівнобедрені, АВ - основа, АВ=16 см, АС=СВ=17 см, = 60°, =90°

Знайти: СВ

 

Розв'язання

1) Розглянемо АСЕ: E = 90°

АЕ =АВ = 8 см, за теоремою Піфагора

СЕ = см,     BE =DE =АВ = 8 см.

2) Розглянемо , за теоремою косинусів

;    см.

Відповідь: відстань між вершинами трикутників 13 см.

 

V. Підведення підсумків.

Домашнє завдання : конспект, [1] ст.48-51, №36, №39, № 46.