Лекція «Квадрат суми та квадрат різниці двох виразів»

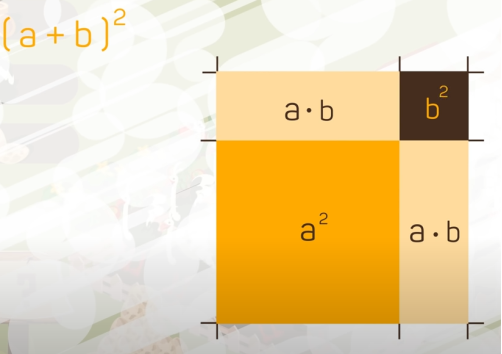
Математика – це не так знання, як уміння

В. Серве

 

Юний друже!

 З лекції  «Квадрат суми та квадрат різниці двох виразів» ти дізнаєшся про формули скороченого множення і навчишся самостійно використовувати дві з них.

Будь уважним/уважною!

 Після засвоєння змісту теми ти:

• матимеш уявлення про альтернативний спосіб помножити многочлен на многочлен в деяких випадках, навчишся розрізняти поняття «скорочене множення» і використовувати формули при розв’язуванні конкретних математичних задач;
• дослідиш доведення формули через геометричний зміст на основі площі квадрата;
• зможеш розв’язувати якісні завдання на спрощення виразів;

• розвинеш логічне мислення, впевненість у власних силах;
• навчишся використовувати формули скороченого множення, застосовувати свої знання і вміння для розв’язування прикладних математичних задач у повсякденному житті.

 

 

План лекції

1. Квадрат суми двох виразів
2. Квадрат різниці двох виразів
3. Застосування формул скороченого множення
4. Для тих, хто бажає дізнатися про ВСЕ

 

1. Квадрат суми двох виразів.

Юний друже, в повсякденному житті часто виникають ситуації пов’язані з обчисленням площі квадрата і прямокутника. Наприклад в архітектурі, у будівництві, навіть при організації ремонту власної оселі. Розглянемо одну з таких задач.

Жив собі дід Панас. Був у нього сад та величенький город для вирощування овочів. Деяку квадратну ділянку зі стороною завдовжки а метрів він засаджував саме картоплею.

Одного разу зателефонувала його онучка Маринка і повідомила, що приїде до нього гостювати на ціле літо.

Пригадав дід Панас, що його улюблениця полюбляє смажену картопельку і вирішив збільшити ділянку картоплі на b метрів.

І замислився: “Який у цьому випадку може бути врожай?”

 

Подумай, як змінилася площа ділянки, відведена під картоплю?

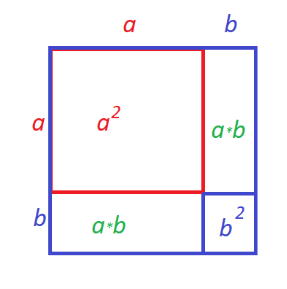
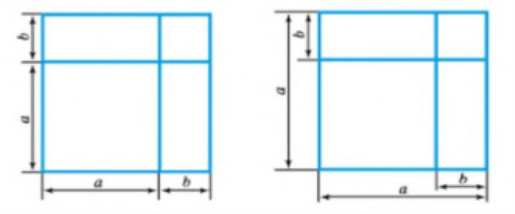
Побудуй у зошиті квадрат зі стороною а клітинок. Олівцем іншого кольору збільши дві сусідні сторони на довжину b клітинок і добудуй новий квадрат.

Склади вираз для обчислення площі нової ділянки для картоплі і перетвори його на многочлен.

Так, дійсно отримуємо вираз (a+b)².

Перетворимо цей вираз на многочлен.

Ти вже вмієш помножити многочлен на многочлен. Пригадай правило множення многочлена на многочлен: щоб помножити многочлен на многочлен, можна кожний член одного многочлена помножити на кожний член другого многочлена й отримані добутки додати.

(a+b)²=(a+b)(a+b)=a²+ab+ba+b²=a²+2ab+b²

Досліди, як пов’язані між собою початковий вираз і відповідь спираючись на свою побудову.

Заміни вирази a і b конкретними числами. Для зразку зроби це з різними парами чисел.

Спробуй розшукати закономірність.

Це і є формула скороченого множення квадрат суми двох виразів. Запиши її в свій довідник.

(a+b)2=a2+2ab+b2

У цій формулі ти бачиш квадрат першого і другого виразу. Одночлен 2ab називається подвійним добутком. Цей термін буде зустрічатися і далі.

Отже, квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвійний добуток першого і другого виразів плюс квадрат другого виразу.

 

2. Квадрат різниці двох виразів

 

Аналогічно розглянемо ситуацію на зменшення “картопляної” ділянки на b метрів.

Подумай, як змінилася площа ділянки, відведена під картоплю?

Побудуй у зошиті квадрат зі стороною а клітинок. Олівцем іншого кольору побудуй ще один внутрішній квадрат зі стороною на b клітинок менше. Починай другий квадрат з кута.

Склади вираз для обчислення площі нової ділянки для картоплі і перетвори його на многочлен.

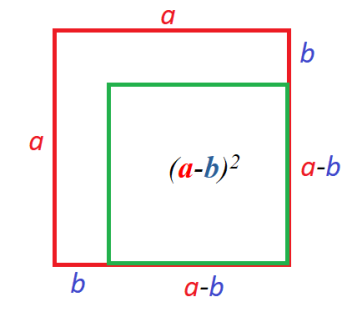
Так, дійсно отримуємо вираз (a-b)².

Перетворимо цей вираз на многочлен.

(a-b)²=(a-b)(a-b)=a² -ab-ba+b²=a²-2ab+b²

Досліди, як пов’язані між собою початковий вираз і відповідь спираючись на свою побудову.

Заміни вирази a і b конкретними числами. Для зразку зроби це з різними парами чисел.

Спробуй розшукати закономірність.

Це є ще одна формула скороченого множення квадрат різниці двох виразів. Запиши її в свій довідник.

(a-b)2=a2-2ab+b2

Пригадай, одночлен 2ab називається подвійним добутком.

Отже, квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвійний добуток першого і другого виразів плюс квадрат другого виразу.

 

3. Застосування формул скороченого множення

Таким чином можна підносити до квадрата суму або різницю будь-яких виразів. За допомогою формул скороченого множення виконати цю дію простіше ніж виконувати множення двох многочленів.

Рекомендую повторити властивості степеня з натуральним показником. Пригадайте:

Розглянемо декілька прикладів. Кожного разу спробуй виконати завдання самостійно, а вже потім опрацьовуй розв’язання!

Приклад 1. Подай у вигляді многочленів вирази:

1) (5a+2b)²;

2) (2c³-3b⁴)².

Зауваження! Скористайся вивченими формулами скороченого множення. Зверни увагу на те, що а і b може подаватися у вигляді будь-якого одночлена або, навіть, многочлена.

Розв’язання:

(5a+2b)²=(5a)²+2·5a·2b+(2b)²=25a²+20ab+4b²

(2c³-3b⁴)²=(2c³)²-2·2c³·3b⁴+(3b⁴)²=4c⁶-12b⁴c³+9b⁸

Приклад 2. Розв’яжи рівняння:

(х+5)²-48=(х-3)².

Зауваження! Скористайся формулами квадрата двочлена, потім можна переносити і зводити подібні доданки.

Розв’язання:

(х+5)²-48=(х-3)²;

х²+10х+25-48=х²-6х+9;

х²-х²+10х+6х=9+23;

16х=32.

Пригадай рівняння виду ах=b, якщо а і b – числа; а не дорівнює нулю. Щоб знайти х потрібно b розділити на а. Іноді буває зручніше скоротити дріб b/а.

16х=32;

х=2.

Відповідь: 2.

 

4. Для тих, хто бажає дізнатися про ВСЕ

Історична довідка.

Ще давньогрецький учений Евклід (близько 325-270 до н. е.) доводив формули квадрата суми та квадрата різниці двох виразів геометричним методом. Розглянь рисунки і спробуй відтворити доведення.

 

Скарбничка ідей

Розглянемо ще один приклад.

Виконайте піднесення до квадрата:

(-х-у)²=(-х)²-2·(-х)·у²+у²=х²+2ху+у².

Але квадрат суми має такий самий результат! Чому так?

 (х+у)²=х²+2ху+у².

Спробуй дослідити, чому однакові результати.

(-х-у)²=( -1·(х+у))²=(-1)²·(х+у)²=(х+у)².

Отже, (-х-у)²=(х+у)².

 

“А що, так можна було?”

Можна легко підносити до квадрату деякі числа з використанням формул скороченого множення. Наприклад:

23²=(20+3)²=400+120+9=529.

198²=(200-2)²=40000-800+4=39204.

 

Шукай і пробуй пізнати цей світ! Ти зможеш!