Урок "Лінійна функція, її графік та властивості"
Урок алгебри в 7 класі
Тема: Лінійна функція, її графік та властивості.
Мета:
- навчальна: ознайомити учнів із «особливими випадками» лінійної функції і її графіком; узагальнити уяву учнів про зв’язок між k та b і графіком; вдосконалювати й читати графіки лінійних функцій;
- розвивальна: розвивати розумову діяльність, логічне мислення, увагу;
- виховна: виховувати позитивне ставлення до предмету, працьовитість, кмітливість, культуру писемного та усного мовлення.
Тип уроку: засвоєння вмінь та навичок.
Обладнання: набір креслярського приладдя; електронний підручник.
Хід уроку
-
Перевірка домашнього завдання. Актуалізація опорних знань.
1. Фронтальне опитування:
- Яку функцію називають лінійною?
- Навести приклад лінійної функції. Вказати коефіцієнти k та b.
- Область визначення лінійної функції.
- Область значень лінійної функції.
- Що є графіком лінійної функції?
- Властивості графіка лінійної функції: якщо k>0, якщо k<0.
- Що показує число b?
- Яку функцію називають прямою пропорційністю?
2. Математичний диктант.
|
В-1 |
В-2 |
|
1) Функція
2) Лінійну функцію задано формулою 3) Графік лінійної функції перетинає вісь Ox під тупим кутом, а вісь Oy в точці (0; -6). Що ви можете сказати про коефіцієнти k та b?
4) Побудуйте графік функції |
1) Функція
2) Лінійну функцію задано формулою 3) Графік лінійної функції перетинає вісь Ox під гострим кутом, а вісь Oy в точці (0; 5). Що ви можете сказати про коефіцієнти k та b?
4) Побудуйте графік функції |
(Після проведення математичного диктанту проводиться взаємоперевірка – робота в парах).
3. Виконаємо побудову графіків функцій.
|
В-1 |
В-2 |
|
|
|
(Після виконання завдання зробити висновки).
-
Формулювання мети і завдань уроку.
З’ясувати, як у загальному випадку пов’язано значення коефіцієнтів k та b із розташуванням графіка лінійної функції в системі координат. Подальша робота з вироблення вмінь працювати із графіком лінійної функції. -
Узагальнення знань.
Виконавши побудову графіків функцій, робимо висновок: якщо в рівнянні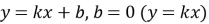 , то графік цієї лінійної функції проходить через початок координат; : якщо в рівнянні
, то графік цієї лінійної функції проходить через початок координат; : якщо в рівнянні 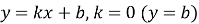 , то графік цієї лінійної функції проходить паралельно осі Ox. Учні записують у зошиті схеми.
, то графік цієї лінійної функції проходить паралельно осі Ox. Учні записують у зошиті схеми.
|
Залежність між розташуванням прямої у = kx + b та значеннями k і b |
||
|
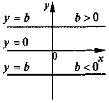
1) k = 0 у = b |
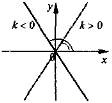
2) b= 0 y = kx |
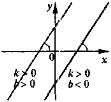
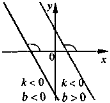
3) y = kx + b (k ≠ 0; b ≠ 0) |
|
|
|
|
-
Закріплення знань. Відпрацювання вмінь.
1. Виконання усних вправ
-
Що являє собою графік функції, яку задано формулою:
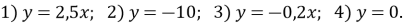
-
Знайдіть координати точки перетину з віссю Oy графіка лінійної функції:
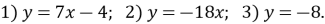
-
Графік лінійної функції пряма, що паралельна осі Ox. Задайте цю функцію формулою, якщо відомо, що її графік проходить через точку:
1) A(5;-2); 2) B(0;7); 3) C(-2;-8).
2. Виконання письмових вправ. Робота з електронним підручником.
№868
Побудуйте в одній системі координат графіки функцій ![]() і
і ![]() та знайдіть координати точок їхнього перетину.
та знайдіть координати точок їхнього перетину.
№874
Не виконуючи побудови, знайдіть координати точок перетину графіків функцій ![]() .
.
№870
Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції ![]() .
.
№872
Не виконуючи побудови графіка функції ![]() , знайдіть точку цього графіка, у якої:
, знайдіть точку цього графіка, у якої:
1) абсциса дорівнює ординаті;
2) ордината на 6 більша за абсцису.
№879
Знайдіть значення b, при якому графік функції ![]() проходить через точку А(-27;4).
проходить через точку А(-27;4).
№881
Графік функції ![]() перетинає осі координат у точках C(0;4) і D(-8;0). Знайдіть значення k і b.
перетинає осі координат у точках C(0;4) і D(-8;0). Знайдіть значення k і b.
- Підсумки уроку.
Охарактеризуйте коефіцієнти k та b у рівнянні лінійної функції, якщо графік цієї функції, зображений схематично, має вигляд:
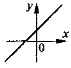

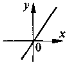

- Домашнє завдання.
§ 23, №869, №871, №875, №880, №887.


про публікацію авторської розробки
Додати розробку