Урок на тему "Графік функції"

Мета:

• Навчальна: сформувати в учнів свідоме розуміння поняття «графік функції» та розпочати роботу із засвоєння вмінь читати та будувати графіки функції, відпрацювати вміння використовувати набуті знання при розв’язуванні вправ;
• Розвивальна: розвивати цікавість учнів до математики, прагнення краще вчити предмет, а також розвивати просторове мислення, відпрацьовувати обчислювальні навички;
• Виховна: виховувати наполегливість та дисциплінованість, а також культуру математичної мови та записів, допитливість, уважність, натхнення, любов до навчання.

Тип уроку: засвоєння нових знань

Задачі уроку:

1.  Сформувати в учнів розуміння поняття «графік функції»

2. Навчити будувати та читати графіки функцій.

3. Оцінити рівень засвоєння учнями знань  та вмінь будувати та читати графіки функцій.

Очікувані результати:

   Діти засвоїли поняття:

   - графік функції,

   - побудова графіка функції.

  Навчилися будувати та читати графіки функцій.

Структура уроку:

1. Організаційний момент (2 хвилини)
2. Перевірка домашнього  завдання (2 хвилин)
3. Актуалізація опорних знань, умінь та навичок (7 хвилин)
4. Виклад нового матеріалу (15 хвилин)
5. Закріплення нового матеріалу(14 хвилин)
6. Підведення підсумку уроку (3 хвилини)
7. Домашнє завдання (2 хвилини)

Хід уроку

1. Організаційний момент

Доброго дня, діти!

(перевірити готовність до уроку)

 Зараз я запишу на дошці дату і тему уроку, а ви, будь ласка, перепишіть їх в зошит. Тепер перевіримо хто сьогодні відсутній. А зараз розпочнемо наш урок.

2. Перевірка домашнього завдання.

  Почнемо з перевірки домашнього завдання.  Вам було все зрозуміло в ньому? (якщо не зрозуміло, розв’язати один з номерів на дошці)

3. Актуалізація опорних знань.

Тепер повторимо з вами раніше вивчений матеріал. Тільки не викрикуйте. Хто знає піднімайте руку. Активні учні отримають хорошу оцінку. Тож давайте розпочнемо.

Дайте відповіді на запитання: (вибіркове опитування з місця)

1. Що називається функцією? 

Змінну у називають функцією від змінної х, якщо кожному значенню змінної х відповідає одне певне значення змінної у.

2. Що називається аргументом функції?

Незалежну змінну х називають аргументом.

3. Які значення утворюють область визначення функції?

Усі значення яких набуває незалежна змінна х утворюють область визначення функції.

4. Які значення утворюють область значення функції?

Усі значення яких набуває залежна змінна у (функція)  утворюють область значення функції.

5. Які ви знаєте способи задання функції?

Формулою (аналітичний), таблично, графіком.

Молодці! Ось ми й згадали, що було вивчене на попередніх уроках. Тепер перейдемо до нової теми, але, щоб трохи відпочити послухайте таке висловлення : багато було відомо давно, але дуже багато є й невідомого. Як в  краплі води можна побачити всі невичерпні скарби океану, так і в шкільному підручнику присутній тисячолітній досвід. Минуле чекає, що ти осягнеш ті знання, які були здобуті великою працею, а майбутнє надіється, що ти внесеш щось нове і передаси своїм нащадкам. Теорія без практики мертва, а практика без теорії неможлива. Для теорії необхідні знання, для практики потрібні вміння. Сьогодні на уроці ми придбаємо знання і  вміння для того, щоб будувати графіки, застосовуючи теорію. 

4. Виклад нового матеріалу

А тепер розпочнемо з вами вивчення нової теми.                   Немає жодної галузі людських знань, куди б не входило поняття функції, її графічного зображення . На попередніх уроках ви вивчили що таке функція та такі способи задання як: задання формулою та таблично.  А сьогодні ми вивчимо графічний спосіб задання. Тема нашого уроку: «Графік функції». Запишіть в зошит тему.                                                                                                   Розглянемо функцію у=0,5, де -3≤ х ≤ 2. Знайдемо значення цієї функції для цілих значень аргументу й занесемо результати в таблицю:

х	-3	-2	-1	0	1	2
у	4,5	2	0,5	0	0,5	2

 

Для цього ми підставляємо значення аргументу у нашу функцію. Далі давайте намалюємо систему координат і позначимо на ній точки, абсциси яких дорівнюють вибраним значенням аргументу, а ординати – відповідним значенням функції.

    

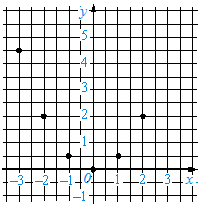
Добираючи інші значення x, що задовольняють нерівності 3  x  2, й обчислюючи відповідні значення y, отримаємо інші пари значень х та у.
Кожній із цих пар також відповідає певна точка на координатній площині. Усі такі точки утворюють фігуру, яку називають графіком функції, заданої формулою y  0,5x², де 3  x  2.

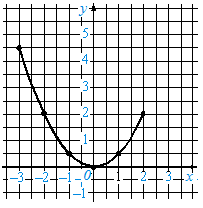
Озн. Графік функції утворюють точки координатної площини, абсциси яких дорівнюють усім значенням аргументу, а ординати  відповідним значенням функції.

Маючи графік функції, можна  знаходити її значення за відомим значенням аргументу і навпаки: знаходити значення аргументу за відомим значенням функції.

Розглянемо, наприклад, функцію, графік якої зображений на рисунку. (Про таку функцію кажуть, що вона задана графічно.)

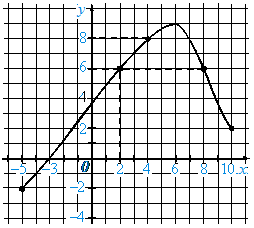
Знайдемо за допомогою графіка значення функції, якщо x  4. Для цього через точку осі x з абсцисою 4 проведемо пряму, перпендикулярну до осі x. Точка її перетину із графіком функції  має  координати  (4; 8). Отже, якщо x  4, то значення функції дорівнює 8. Знайдемо за допомогою цього ж графіка значення аргументу, для яких значення функції дорівнює 6. Для цього через точку осі у з ординатою 6 проведемо пряму, перпендикулярну до осі у. Одержимо дві точки її перетину із графіком функції: (2; 6) і (8; 6). Отже, функція набуває значення 6, якщо x  2 або x  8. Зрозуміло? (якщо ні, то пояснити ще раз)

На даному графіку можна побачити, що

1) Область визначення функції утворюють усі значення х, що задовольняють нерівності 5  x  10.

2) Найбільше значення функції дорівнює 9

3) Найменше значення функції дорівнює 2

4) Область значень функції утворюють усі значення у, що задовольняють нерівності 2  у  9.

5) Значення функції дорівнює нулю, якщо х  3. Ті значення аргументу, для яких значення функції дорівнюють нулю, називають нулями функції. Отже, значення х  3 є нулем даної функції.

6) Функція набуває додатних значень, якщо 3 < x  10; від’ємних значень — якщо 5  x < –3.  

(показати це все на графіку)

 Тепер давайте з вами розглянемо приклади на сторінці 126.

Приклад 1. Побудувати графік функції, заданої формулою:

 а) y  0,5x + 1, де 4  x  4, склавши таблицю значень функції з кроком 1;  б) y  1 – x², де 2  x  2.

Складемо таблицю значень функції:

 

x	4	3	2	1	0	1	2	3	4
y	1	0,5	0	0,5	1	1,5	2	2,5	3

 

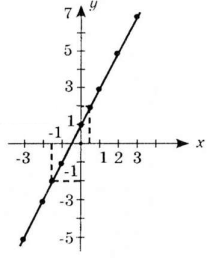
Позначимо точки, координати яких подані в таблиці, на координатній площині. Якщо до цих точок прикласти лінійку, то побачимо, що всі вони лежать на одній прямій. Сполучимо відрізком крайні позначені точки. Цей відрізок і є графіком функції y  0,5x + 1, де 4  x  4.

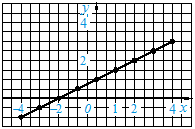
 Я зображую на дошці графік, а ви будь ласка зробіть це ж саме в зошиті. Добре. Тепер розглянемо приклад 3 з підручника.

Приклад 3.  На рисунку зображено графік функції. Користуючись графіком, заповнити таблицю:

x	6	2	8
y				4	1,5	1

 

 Давайте заповнимо таблицю:

 

x	6	2	8	6	5;  8	4  x  1;   6
y	4	1	1,5	4	1,5	1

 

Всі вже справились з завданням?

5. Закріплення нового матеріалу

Для того,щоб ви краще змогли зрозуміти новий матеріал  розв’яжемо з вами декілька прикладів.

(викликати до дошки  учнів, по черзі).

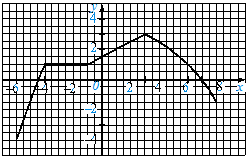
№ 801. Функція задана графіком.

а) Знайдіть значення функції, якщо х  4; х  –2; х  2.

            Відповідь: у= -3; у= -2; у= 1

 б) Знайдіть значення аргументу, якому відповідає значення функції у  2; у  0; у  3.

           Відповідь:  х= -2; х=1; х= 3.

 в) Яка область визначення та область значень функції?

           Відповідь:  Область визначення   -4< x < 3

                               Область значень        -3 < у < 3

 г) Чому дорівнюють найбільше та найменше значення функції?

           Відповідь: найбільше  3

                              найменше  -3

 д) Вкажіть нулі функції.

          Відповідь:  х=1

 е) Для яких значень х функція набуває додатних значень; від’ємних значень?

      Відповідь:  х = -4;  х=3

 

Добре! Хто тепер бажає до дошки? Викликати бажаючих (якщо таких немає, викликати слабших учнів). Ті хто зробить в зошиті швидше, ніж на дошці піднімайте руку і я підійду перевірю.

№803. На рисунку  зображено графік функції. Користуючись цим графіком, заповніть таблицю:

x	3	2	0	1	4,5
y						1,5	–1	0	4

 Яка область визначення та область значень функції? Чому дорівнює найменше значення функції? Для яких значень х функція набуває додатних значень?

 

Розв’язання

x	3	2	0	1	4,5	2	1	0;4	-3
y	4	2	0	-1	1,5	1,5	–1	0	4

 

Область визначення -3< х < 5

Область значення -1,5 < у < 4

Найменше значення функції (2; -1,5)

Функція набуває додатних значень для х [-3;0][4;5]

 Наступний №805. Хто піде до дошки?

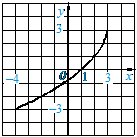
№ 805. Побудуйте графік функції, заданої формулою y  2x + 1, де 3  x  3, склавши таблицю значень функції з кроком 1. Чи належать графіку
функції точки A(2; 3), B(0; 1)? Користуючись графіком, знайдіть: значення функції, якщо х  1,5; х  0,5; значення аргументу, якому відповідає значення функції у  0; у  1.

 

Розв’язання:

x	3	2	-1	0	1	2	3
y	-5	-3	-1	1	3	5	7

   

A(2; 3)    у=2*(-2)+1=-3  належить графіку

B(0; 1)       у=2*0+1=1  не належить графіку

7. Підведення підсумку уроку.

Тепер повторимо, що ми вивчили за урок.

1. Що ви вивчили сьогодні на уроці?

 Що таке графік функції, як його будувати, читати графіки функції, нулі функції.

2. Які точки утворюють графік функції?

Графік функції утворюють точки координатної площини, абсциси яких дорівнюють усім значенням аргументу, а ординати  відповідним значенням функції.

2. Які значення називають нулями функції?

Ті значення аргументу, для яких значення функції дорівнюють нулю, називають нулями функції.

Молодці! Всі ви сьогодні дуже добре попрацювали. Дайте щоденники на оцінки. Я думаю, що сьогодні на уроці ви добре засвоїли новий матеріал. На наступному уроці ми з вами ще порозв’язуємо приклади з цієї теми.

8. Домашнє завдання

   А зараз відкрийте щоденники і запишіть завдання додому. Вивчити ст. 123-125, повторити параграф 23 та розв’язати

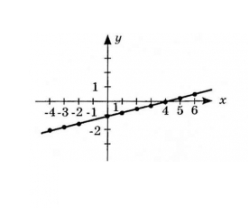
№807. Побудуйте графік функції, заданої формулою:

 а) y   де 4  x  6;

Розв’язання:

Складемо таблицю

х	-4	-3	-2	-1	0	1	2	3	4	5	6
у	-2	-1,75	-1,5	-1,25	-1	-0,75	-0,5	-0,25	0	0,25	0,5

 

Побудуємо графік:

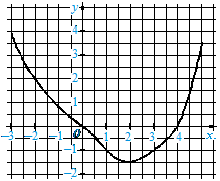
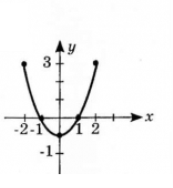
б) y  x² – 1, де 2  x  2.

 

Розв’язання:          Складемо таблицю

x	2	1	0	1	2
y	3	0	-1	0	3

 

Побудуємо графік:

 

 

 

 

 

 

Міністерство освіти і науки, молоді та спорту України

Полтавський національний педагогічний університет

ім. В. Г. Короленка

 

 

 

 

 

 

План-конспект

уроку з геометрії на тему:

“ Сума кутів трикутника”

 

 

 

 

 

 

 

 

 

підготувала студентка

групи М-42

фізико-математичного факультету

Пусан Вікторія

Методист: Черкаська Любов Петрівна

 

 

 

 

 

 

 

Полтава 2013