Урок "Лінійна функція її графік та властивості."(+презентація)

Тема уроку: Лінійна функція її графік та властивості.

Мета уроку:

навчальна: повторити, систематизувати та узагальнити матеріал з теми «Лінійна функція, її графік та властивості», продовжити формування вмінь та навичок застосовувати знання з теми до розв’язування стандартних та нестандартних задач; розкрити прикладне значення лінійної функції.  

розвивальна: формувати вміння аналізувати й узагальнювати інформацію, виділяти головне,  розвивати навики творчо-пошукової, самостійної роботи, виробити у школярів практичні навички під час побудови графіків функції;

виховна: виховати активну життєву позицію, відчуття успіху, любов до математики.

Тип уроку: урок узагальнення та систематизації знань, умінь та навичок

Оформлення уроку: на дошці написані тема уроку, епіграф.

Міжпредметні зв’язки: біологія, фізика, економіка.

Епіграф уроку: «Немає жодної галузі людського знання, куди не входили б поняття про  функції та їх графічне зображення» (К. Ф. Лебединцев)

Хід уроку

І. Організаційний момент (слайд №2)

ІІ. Перевірка домашнього завдання (слайд №3)

Обговорити  допущені учнями помилки виявлені за допомогою програми

https://www.geogebra.org/graphing/bef4bcmj

https://www.geogebra.org/graphing/mmbwfrnn

ІІІ. Повідомлення теми, мети, завдань уроку,  мотивація навчальної та пізнавальної діяльності учнів (слайд №4,5)

Бесіда

Одне з найважливіших понять математики – функція. За її допомогою моделюють і досліджують різноманітні процеси, що відбуваються навколо нас. Коли росте дитина, змінюються її зріст, об’єм, маса; коли злітає літак, змінюється його швидкість, відстань від поверхні землі, маса пального в баках; коли будують висотний будинок, змінюється його висота, маса, вартість. Усі такі процеси зручно моделювати за допомогою функцій. Функція – математична модель реальних процесів.

Повторимо, систематизуємо та узагальнимо матеріал з теми «Лінійна функція, її графік та властивості», продовжимо формування вмінь та навичок застосовувати знання з теми до розв’язування стандартних та нестандартних задач і  спробуємо розкрити прикладне значення лінійної функції.

ІV. Узагальнення  та систематизація знань (слайд №6-7)

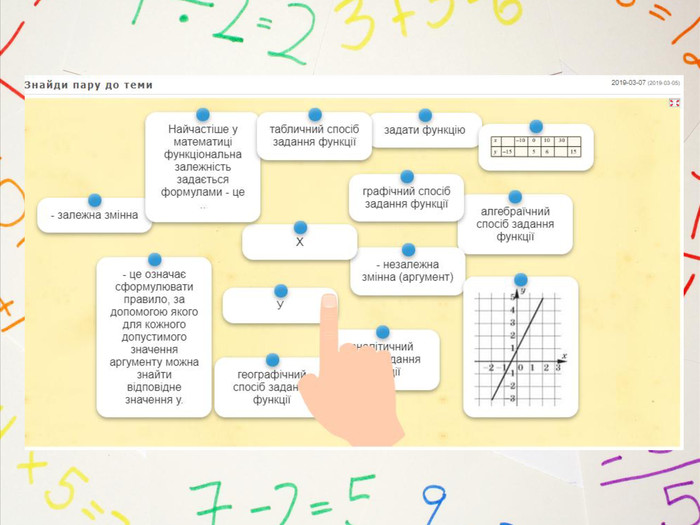
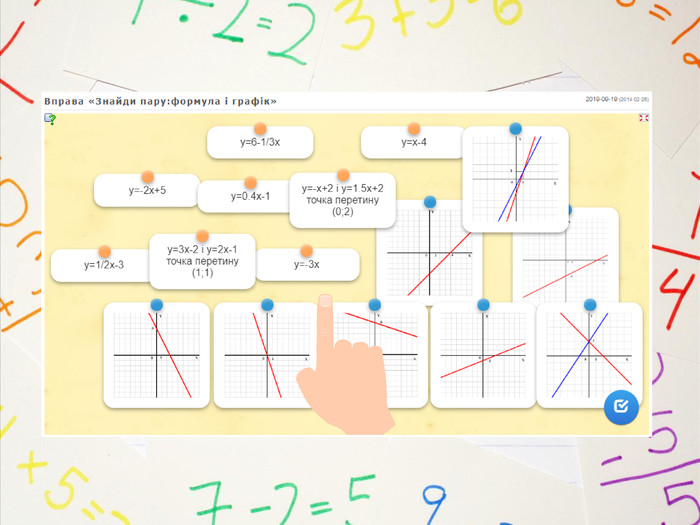
Вправа «Знайди пару» в сервісі інтерактивних вправ Learning Apps https://learningapps.org/6767306

https://learningapps.org/display?v=p7x5i33at

V. Удосконалення вмінь і навичок (презі-слайд №8)

Щоб активізувати уявлення про функціональну залежність як математичну модель реальних процесів, розв’яжемо наступну задачу:  

Опівночі температура повітря була -1°С. До 7 години температура знижувалась  рівномірно на 2°С за кожну годину

1. Запишіть формулу, яка виражає зміну температури повітря (у) залежно від змінної часу (х);
2. Побудуйте графік залежності температури від часу; (за допомогою програми)

Знайдіть за допомогою графіка температуру повітря: о 2 годині, о 6 годині, о 7 годині.

https://www.geogebra.org/graphing/nyeqzgv9

«Наше фізичне здоров’я, соціальне щастя і економічний добробут підтримаємо лише ми самі у спільній праці, будучи вдумливими, ефективними доглядачами наших природних ресурсів».

(Рональд Рейган)

Щоб розкрити прикладне значення лінійної функції зараз кожна група обере галузь знань, розв’яже завдання та здійснить його захист.

Письмові вправи

Повторення правил роботи в групі: слайд 8

• Працюють усі;
• Кожний пропонує варіант відповіді по черзі;
• Говорити коротко й чітко. Головне – не перебивати один одного;
• Критикувати не товариша, а ідею;
• Працювати разом, щоб було добре всім;

Культурна людина вміє не тільки говорити, а й слухати.

(слайд 9)

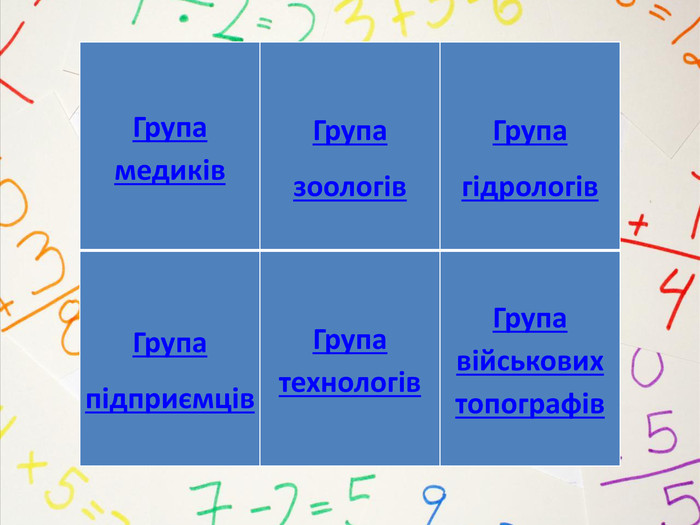
Група медиків

Задача . Медичними працівниками встановлено, що для нормального розвитку дитини, якій х років (х<18), вона повинна спати t год на добу, де t визначається за формулою: t=16 - х/2. Знайдіть t(5), t(10),  t(14). Знайти вік дитини, яка повинна спати 10год.

(Відповідь: 13,5год, 11год, 9 год., 12 років)

Повноцінний сон необхідний для нормального росту й розвитку, особливо в період підвищення навчального навантаження. Постійні «недосипання» призводять до погіршення загального стану, головного болю, зниження імунітету та пам’яті.

https://www.geogebra.org/graphing/kqmn5na3

Група підприємців

Задача. За 15кг макулатури можна отримати 18грн., а за 25кг – 30грн. Знайдіть графічно, скільки грошей можна отримати за 5кг, 10кг, 30кг макулатури, вважаючи, що ціна прийому 1кг макулатури стала.

https://www.geogebra.org/graphing/f2yvhdet

Група зоологів

Задача. Чисельність зубрів в заповіднику може бути знайдена за формулою: y = 50 +3t, де y кількість особин, а t час (у роках). Знайдіть, скільки особин буде в даному заповіднику через 3 роки. Через скільки років в цьому заповіднику особин буде 65 штук?

(Відповідь: 59 зубрів, через 5 років)

https://www.geogebra.org/graphing/vrstan2r

Група гідрологів

Задача . Рівень води в річці на початку спостережень був на 12 см нижчий від звичайного рівня, а потім щоденно підвищувався на 3 см.

1) запишіть формулу, яка виражає залежність рівня води (у) від часу (х);

2) побудуйте графік цієї залежності;

3) знайдіть, користуючись графіком, через скільки днів від початку спостережень рівень води досяг звичайного рівня.

(Відповідь: у=3х-12; через 4 дня)

https://www.geogebra.org/graphing/tnyqakfa

Група технологів

Конкретною моделлю функції y = kx + b є залежність калорійності молока від жирності, виражена формулою k = 9 a + 30, де k – калорійність молока в калоріях, a – відсоток жиру в молоці.

Знайдіть значення k при значеннях аргументу a, що дорівнює  2%; 2,5%, 3,5%, 6%.

Побудуйте графік залежності калорійності молока від жирності.

(Відповідь:

k = 9 a + 30

https://www.geogebra.org/graphing/gdutf8y5

Група військових топографів

Дві роти десантників, що атакують, наступають за законом:

і    

. Дайте відповідь на запитання: чи відбудеться зустріч наступаючих і де саме.

Відповідь:

у=3х-2

у=0,5х+3

Зустріч десантників відбудеться у точці

(2;4) – це точка перетину графіків функцій, що задають рух груп десантників

https://www.geogebra.org/graphing/at2djfxz

VІ. Підсумок уроку.

 Онлайн тестування

https://naurok.com.ua/test/testi-liniyna-funkciya-grafik-ta-vlastivosti-32485.html

VІІ. Рефлексія.

Рефлексійна мішень

• - все зрозумів / зрозуміла

• -  майже все зрозумів / зрозуміла

• -  нічого не зрозумів / не зрозуміла

VІІІ. Домашнє завдання https://naurok.com.ua/test/liniyna-funkciya-31425.html