Урок "Лінійна функція та її графік"
ЛІНІЙНА ФУНКЦІЯ ТА ЇЇ ГРАФІК (7 клас)
Тип уроку: Урок формування знань, умінь та навичок.
Вид уроку: Урок-практикум із застосуванням інтерактивних прийомів навчання.
Форма роботи: Фронтальна, групова, індивідуальна робота.
Мета:
Навчальна: Узагальнити та систематизувати базові знання учнів по темі “ Функція. Лінійна функція. Її графік і властивості ”, формувати навички читання та побудови графіків лінійної функції; визначати можливості взаємного розміщення графіків лінійних функцій.
Розвиваюча: Розвивати навчальні інтереси, здібності на основі розумових дій; формувати навички аналізу, систематизації, узагальнення.
Виховна: Виховувати активну позицію в навчанні і житті; сприяти розвитку математичної культури учнів; формувати навички спільної діяльності.
Обладнання: Роздатковий матеріал.
«… Покажи мені - і я запам'ятаю, дай мені діяти самому - і я навчусь…»
Китайска мудрість
Хід уроку:
- Організаційний момент (психологічне налаштування на співпрацю):
Китайська мудрість гласить: «… Покажи мені - і я запам'ятаю, дай мені діяти самому - і я навчусь…»
То ж дійте, думайте, питайте, пропонуйте – бо тільки таким шляхом ми зможемо пізнати істину.
2. Оголошення теми та мети уроку:
На попередніх уроках ми з вами розглянули загальні відомості про функцію, її властивості та графік, почали знайомство з лінійною функцією. Сьогодні ми продовжуємо вивчати лінійну функцію: ми будемо вчитися читати її графік, будувати графік лінійної функції; й визначимо взаємне розміщення графіків двох лінійних функцій, побудованих в одній системі координат.
3. Актуалізація опорних знань:
Давайте всі разом розшифруємо народну мудрість, зашифровану на дошці: У кожного з вас є картка, на якій вказано координати точок. Знайдіть її в координатній площині і дізнаєтесь літеру (Букви в координатній площині українські). Назвіть номер своєї картки і літеру, що ви знайшли. (додаток 1)
Перед розв’язком:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
11 |
|
12 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
|
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Після розв’язку:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
11 |
|
12 |
13 |
|
М |
У |
Д |
Р |
И |
М |
Н |
І |
Х |
Т |
О |
Н |
Е |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
|
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
В |
Р |
О |
Д |
И |
В |
С |
Я |
А |
Н |
А |
В |
Ч |
И |
В |
С |
Я |
Хай ця народна мудрість допоможе вам визначити основні орієнтири у вашому житті.
А тепер давайте пригадаємо основні теоретичні положення:
(технологія «Галегея», «Броунівський рух»):
- Що ви знаєте про функцію?
(означення функції, означення графіка функції, область визначення, область значень, аргумент, функція, способи задання функції)
- Що ви знаєте про лінійну функцію?
(означення, графік, кутовий коефіцієнт, пряма пропорційність)
Усні вправи:
Задано функції:
1)![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]()
- Які з даних функцій є лінійними?
- Назвіть коефіцієнти лінійних функцій.
- Які з даних функцій задають пряму пропорційність?
- Графіки яких функцій проходять через початок координат?
- Графіки яких функцій мають лише одну точку перетину з осями координат?
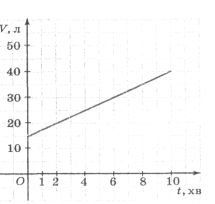
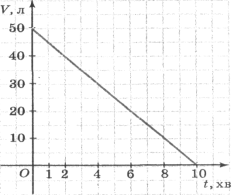
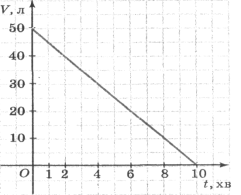
(Додаток 2) На малюнках 1 і 2 зображено два графіки:
на одному — процес наповнення бака водою, а на другому — процес витікання води з бака. По кожному графіку дайте відповіді на запитання:
1) На якому з малюнків який процес зображено?
2) Скільки літрів води було у баку в початковий момент часу?
3) Скільки літрів води було в баку через 1 хв; через 6 хв; через 8 хв?
4) Через скільки хвилин у баку було 25 л води?
5) Чи задають дані графіки лінійні функції?
6) Назвіть точки перетину графіків з осями координат.
7) Назвіть область визначення та значень кожної функції.
4. Математичний диктант (Отримані відповіді підчеркніть)
-
Назвіть кутовий коефіцієнт функції
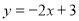 ( k = -2)
( k = -2)
- Скільки точок графіка лінійної функції потрібно знайти, щоб побудувати її графік (Дві)
-
Гострий, тупий чи прямий кут утворює графік функції
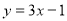 з додатним напрямком осі Ох? (Гострий)
з додатним напрямком осі Ох? (Гострий)
-
Функція задана формулою
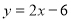 . Чи проходить графік цієї функції через т.А(2; -2)? (Так)
. Чи проходить графік цієї функції через т.А(2; -2)? (Так)
-
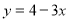 . Знайдіть значення функції, якщо значення аргументу дорівнює -1? (
. Знайдіть значення функції, якщо значення аргументу дорівнює -1? (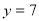 )
)
-
Знайдіть нулі функції
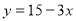 . (
. (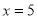 )
)
(взаємоперевірка отриманих результатів: правильні результати – на звороті дошки)
Хто не допустив жодної помилки? Допустив одну помилку? - дві? - більше?
Оцініть кожне правильно розв’язане завдання в 2 бали; за помилку обчислювального характеру в завданні за умови, що ідея розв’язання завдання була правильною поставте 1бал. У разі неправильного виконання завдання – 0 балів.
Хто отримав 12 балів? 11? 10? 9? Хто отримав оцінку нижче 8 балів вам слід ще раз ретельно переглянути теоретичний матеріал підручника та запропоновані автором вправи з рубрики «Прочитайте»
ПРАКТИЧНА РОБОТА
(робота в парах)
- Побудуйте графіки функцій в одній системі координат:
![]() 1)
1) ![]() ; 1)
; 1) ![]() ;
;
2) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() . 3)
. 3) ![]() .
.
2. Порівняйте відповідні коефіцієнти функцій 1) і 2) та визначте, як розміщені графіки цих функцій (перетинаються чи паралельні?).
Порівняйте відповідні коефіцієнти функцій 2) і 3) та визначте, як розміщені графіки цих функцій (перетинаються чи паралельні?).
Порівняйте відповідні коефіцієнти функцій 1) і 3) та визначте, як розміщені графіки цих функцій (перетинаються чи паралельні?).
3. Зробіть висновок.
4. Ознайомтесь з результатами роботи групи, яка виконувала інший результат.
5. Узагальніть ваші результати.
6. Визначте, як розміщені графіки функцій:
1) ![]() і
і ![]() ;
;
2) ![]() і
і ![]() ;
;
3) ![]() і
і ![]() ;
;
4) ![]() і
і ![]() .
.
(Вадповіді до п.6: 1), 4) - перетинаються; 2), 3) - паралельні)
7. Узагальніть, які способи можна застосувати для визначення взаємного розміщення графіків лінійних функцій.
(Побудувати графіки даних функцій в одній системі координат і визначити взаємне розміщенння прямих на координатній площині або порівняти коефіцієнти при «х»: якщо коефіцієнти при «х» однакові, а вільні члени різні, то графіки перетинаються; якщо коефіцієнти при «х» та вільні члени заданих функцій рівні, то графіки співпадають (накладаються один на один); якщо коефіцієнти при «х» не рівні, то графіки даних функцій перетинаються)
Розв’язування вправ: (підручник Янченко )
№ 846 (а) : (Знайдіть координати точок перетину графіка функції ![]() з осями координат та нулі функції.)
з осями координат та нулі функції.)
Розв’язання:
З Ох: Тоді у=0, отже: ![]() . Звідси х=2,5 (2,5; 0);
. Звідси х=2,5 (2,5; 0);
З Оу: Тоді х=0, отже у=![]() . Звідси у=4 (0; 4).
. Звідси у=4 (0; 4).
Нулі функції: у=0, отже: ![]() . Звідси х=2,5 х=2,5.
. Звідси х=2,5 х=2,5.
Відповідь: (2,5; 0); (0; 4); х=2,5 .
№ 851 (Задайте формулою пряму пропорційність, якщо відомо, що її графік проходить через точку: 1) (1; 17); 2) (-2; -4).)
Розв’язання:
1)![]() ; х=1; у=17 Тоді 17=
; х=1; у=17 Тоді 17=![]() , звідси
, звідси ![]() . Отже,
. Отже, ![]() .
. ![]()
2)![]() ; х=-2; у=-4 Тоді -4=
; х=-2; у=-4 Тоді -4=![]() , звідси
, звідси ![]() . Отже,
. Отже, ![]() .
. ![]() .
.
3 863 (а) ( Не виконуючи побудов, знайдіть координати точки перетину графіків функцій ![]() ;
; ![]() .)
.)
Розв’язання:
Графіки функцій ![]() ;
; ![]() за умовою перетинаються, отже, 14х-8=7х+8, звідси 7х=16; х=
за умовою перетинаються, отже, 14х-8=7х+8, звідси 7х=16; х=![]() . Тоді
. Тоді ![]() . Звідси,
. Звідси, ![]() - точка перетину графіків.
- точка перетину графіків.
Відповідь: ![]() .
.
Запишіть домашнє завдання:
Д/з: Янченко: № 845; № 847 (а); № 850 (а); (обговорення). Додатково № 864 (продумати два способи розв’язання завдання)
Підсумок уроку:
Узагальнення результатів діяльності на уроці:
А тепер давайте підведемо коротенький підсумок уроку:
Поділіться, що нового ви дізналися на уроці, які отримали враження, емоції від нашого сьогоднішнього уроку.
1) Продовжте речення: (Учні висловлюються по черзі, починаючи речення з слів, записаних на розвороті дошки)
На цьому уроці….
Для мене було….
Я навчився….
Я дізнався….
2) Заповніть лист самоконтролю:
Все, що розглядалось на уроці, я зрозумів на ______ %
Чи збагатив мене урок новими знаннями: Так Ні ( потрібне підкресліть)
Я працював на уроці на ______% і заслуговую оцінку _________
Чи потрібна мені буде допомога при виконанні домашнього завдання: Так Ні
Ми вже з вами на початку уроку звертались до джерел народної мудрості, тож пам’ятайте, що саме від вас залежить з яким багажем життєвої мудрості та знань ви станете на стежину свого власного самостійного дорослого життя. І пам’ятайте,
ЩО НИНІ УТЕЧЕ, ТО ЗАВТРА НЕ ЗЛОВИШ
Додаток 1
|
1.
(3; 4) |
2.
(-1; 2) |
|
3.
(1; 0) |
4.
( 0; 5) |
|
5.
(-4; 0) |
6.
(3; 4) |
|
7.
(0; -2) |
8.
(2; -1) |
|
9.
(4; 1) |
10.
(-2; -3) |
|
11.
(3; -3) |
12.
(0; -2) |
|
13.
(6; 0) |
14.
(-5; 6) |
|
15.
(0; 5) |
16.
(3; -3) |
|
17.
(1;0) |
18.
(-4;0) |
|
19.
(-5; 6) |
20.
( -3;-5) |
|
21.
(-3; 3) |
22.
(2; 3) |
|
23.
(0; -2) |
24.
(2; 3) |
|
25.
(-5; 6) |
26.
(5; 3) |
|
27.
(-4; 0) |
28.
(-5; 6) |
|
29.
(-3;-5) |
30.
(-3; 3) |
|
31.
|
32.
|

 Додаток 2
Додаток 2
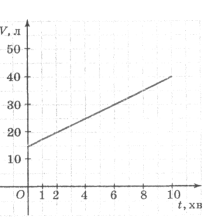
Рис. 1 Рис. 2
ПРАКТИЧНА РОБОТА
-
 Побудуйте графіки функцій в одній системі координат:
Побудуйте графіки функцій в одній системі координат:
1) ![]() ; 1)
; 1) ![]() ;
;
2) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() . 3)
. 3) ![]() .
.
2. Порівняйте відповідні коефіцієнти функцій 1) і 2) та визначте, як розміщені графіки цих функцій (перетинаються чи паралельні?).
Порівняйте відповідні коефіцієнти функцій 2) і 3) та визначте, як розміщені графіки цих функцій (перетинаються чи паралельні?).
Порівняйте відповідні коефіцієнти функцій 1) і 3) та визначте, як розміщені графіки цих функцій (перетинаються чи паралельні?).
3. Зробіть висновок.
4. Ознайомтесь з результатами роботи групи, яка виконувала інший результат.
5. Узагальніть ваші результати.
6. Визначте, як розміщені графіки функцій:
1) ![]() і
і ![]() ;
;
2) ![]() і
і ![]() ;
;
3) ![]() і
і ![]() ;
;
4) ![]() і
і ![]() .
.
7. Узагальніть, які способи можна застосувати для визначення взаємного розміщення графіків лінійних функцій.


про публікацію авторської розробки
Додати розробку
