Урок "Лінійна функція та її застосування"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Лінійна функція та її застосування

Інтегрований урок з алгебри. 7-й клас

 

Мета:

Освітня:

1. Закріплення понять лінійної функції, прямої пропорційності, властивостей даних функцій.
2. Систематизація знань з даної теми.
3. Продовження формування умінь планувати навчальну роботу з книгою, формування навичок самоконтролю.
4. Застосування прикладів з навколишньої дійсності як моделей математичних залежностей.
5. Уміння показати єдність теорії математики та інших наук через міжпредметні зв'язки.

Виховна:

Забезпечити умови для:

• Виховання  акуратності.
• Виховання відповідального відношення до навчання.
• Виховання культури спілкування.

Розвиваюча:

Забезпечити умови для:

• Самостійного добування знань, осмисленого відношення до своєї діяльності.
• Розвитку просторової уяви.
• Самостійності мислення: виділяти головне, бачити загальну закономірність і робити узагальнені висновки.
• Формування культури навчальної діяльності.
• Особистісного саморозвитку учнів.
• Розвитку критичного мислення.
• Розвитку окоміру учнів.
• Розвиток самостійності.

Методи: репродуктивний, частково-пошуковий, груповий (учні об’єднані у 4 групи).

Слайд 1. Епіграф.

«Тисячі нерозгаданих таємниць таїть у собі наука, і без вас, без вашої молодості, сміливості, ентузіазму, вони не будуть розгадані. Наука чекає вас, друзі»

Академік О.М. Несміянов

Цього року  ви уже семикласники. І саме 7-й клас – самий незвичайний рік навчання.

Цінний, важливий і цікавий він тим, що тут ви познайомилися з двома областями математичної науки: алгеброю і геометрією, почали вивчати фізику та хімію.

Як ви думаєте, чи існує взаємозв'язок між цими науками.

 

 

 

 

 

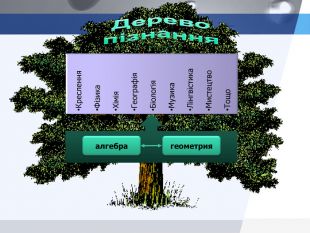
Слайд 2. «Дерево пізнання».

Алгебра і геометрія на ньому розташовані так близько один від одного, що алгебраїчні і геометричні способи розв’язання задач переплітаються, немов гілки цього дерева.

Живильним соком алгебри і геометрії насичуються інші науки, яких у розкішній кроні математичного дерева так багато.

Слайд 3. Математичний більярд.  Групи учнів обирають номер питання.

1. Сформулюйте означення лінійної функції.

(Лінійної називається функція, яку можна задати формулою виду у= kх +b, де х - незалежна змінна, k і b - деякі числа)

2. Які окремі випадки лінійної функції вам відомі? (Перший випадок, коли число b дорівнює 0. Другий випадок, коли число k дорівнює 0)
3. Як називається функція, у якої число b дорівнює 0? Дайте її визначення. (Така функція називається прямою пропорційністю. Прямою пропорційністю називається функція, яку можна задати формулою виду у= kх , де х - незалежна змінна, k – число, що не дорівнює нулю.)
4. Якою формулою задається функція, в якої число k дорівнює нулю? (Така функція задається формулою виду у = b)

Слайд 4.

Згрупуйте лінійні функції.

у = 2х – 3, у = 6, у = 7 х, у = , у = - х, у = - 12, у = 0, у = х

• Чи є дані функції лінійними?
• Що було основою класифікації функцій? (Види функцій)
• Назвіть числа k і b у формулах лінійних функцій.
• Додайте по одному прикладу в кожну групу.

Слайд 5. Математичний більярд.

5. Що є графіком лінійної функції? (Графіком лінійної функції є пряма)
6. Чому для побудови графіка лінійної функції досить тільки двох точок? (З початкових геометричних відомостей ми знаємо, що через дві точки площини можна провести пряму і до того ж тільки одну)
7. Через яку точку проходить графік лінійної функції? (Графік лінійної функції проходить через точку з координатами (0; b))
8.  Що означає твердження: «точка належить графіку функції»? (Дане твердження означає, що абсциса цієї точки дорівнює аргументу, а ордината - відповідному значенню функції)

Слайд 6.

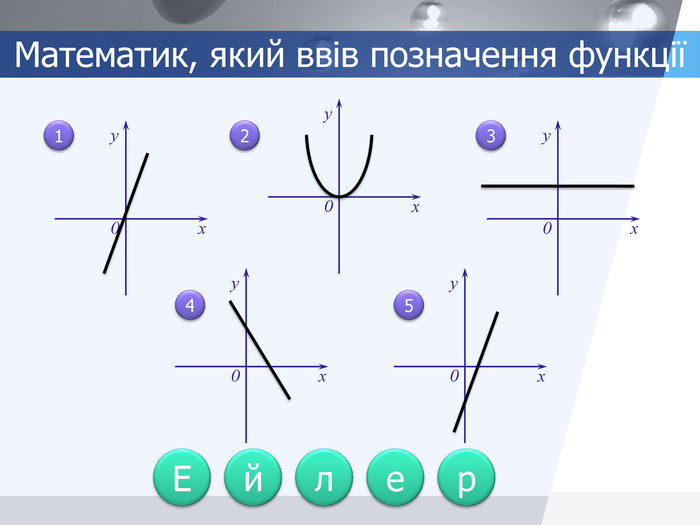
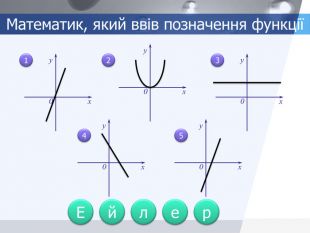
На слайді п'ять графіків функцій. Давайте довідаємося ім'я одного математика, що ввів аналітичне позначення функцій. Для цього відповімо на питання (кожному графіку відповідає своя буква) (мал.1):

1. Який графік функції зайвий? Чому?
2. На якому малюнку зображений графік прямої пропорційності? Чому?
3. На якому малюнку зображено графік функції, у якої k0, b<0?
4. На якому малюнку зображено графік функції, у якої k0, b>0?
5. На якому кресленні пряма паралельна осі абсцис? Як вона задається аналітично?

 

 

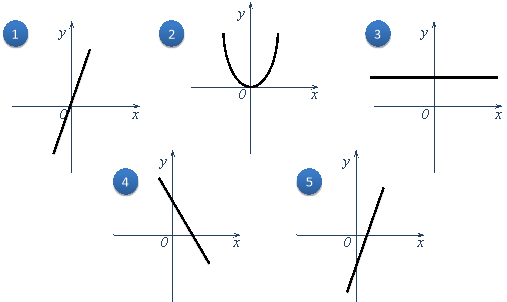
Одержуємо: Ейлер. Аналітичне позначення функції ввів Ейлер.

 

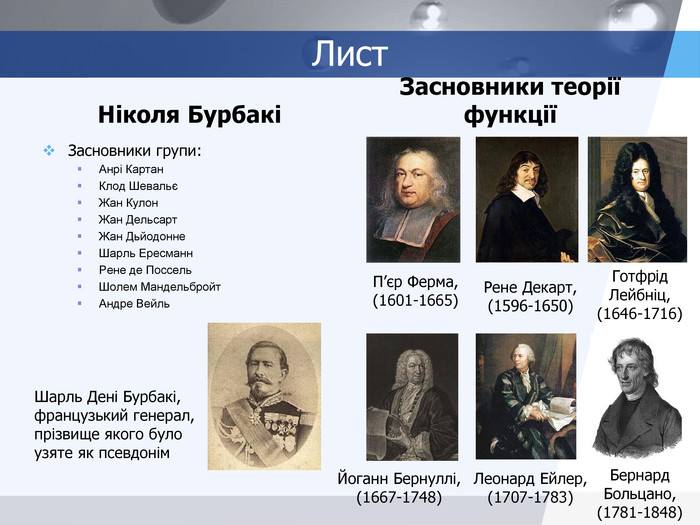
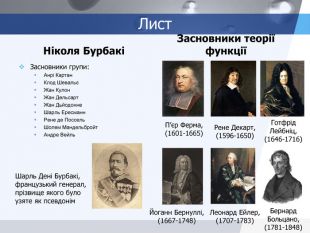
Слайд 7. Історична довідка.

Учитель. Сьогодні на урок, на який виноситься питання: «Лінійна функція у задачах з фізики, механіки та топографії, економіки та бізнесу, біології та медицини», надійшов лист від групи вчених, які іменують себе псевдонімом Ніколя Бурбакі. Слово для ознайомлення із листом надається одному із вчених цієї групи.

Вчений. «Ми, група вчених Ніколя Бурбакі – вдячні французам П’єру Ферма, Рене Декарту за розгляд функції як залежності ординати точки від її абсциси, Готфріду Лейбніцу – жителю німецького королівства ХVII століття за введення терміну «функція», швейцарам Йоганну Бернуллі та Леонарду Ейлеру за розгляд функції як аналітичного виразу, чеському математику Бернарду Больцано, який записував функцію як залежність однієї змінної від іншої, а також всім тим, чиї ідеї стали для нас тим ґрунтом, на якому проросли наші ідеї, які змогли довести до логічного завершення найзагальніше сучасне означення поняття «функції». Розв’язування завдань за допомогою функцій продуктивні і спільні для багатьох галузей знань. Функціональні залежності проникають в різні сфери наук та виробничої діяльності. Тому ми звертаємося із цією заявою до Вас, учні 7-А класу Станіславської загальноосвітньої школи І-ІІІ ступенів ім. К.Й. Голобородька, щоб ви дослідили і проаналізували:

• як глибоко зуміла проникнути функція у науку, економіку, виробництво;
• чи вмієте ви, наші праправнуки, на практиці застосовувати набуті знання про функцію;
• який рівень знань, умінь і навичок молодого покоління, яке розвиватиме науку і суспільство на початку ХХІ століття;
• чи не були марними наші досягнення?»

Слайд 8. Робота в групах різних галузей знань. Галузь обирають учні.

Учитель. Сьогодні, ви, молоде покоління, повинні розкрити прикладне значення лінійної функції. Для цього кожна група обере галузь знань, розв’яже завдання та здійснить захист цього завдання.

 

 

Завдання (учитель до уроку визначається із кількістю груп).

Для групи метеорологів:

Швидкість поширення звуку в повітрі в залежності від температури може бути знайдена за формулою: v = 331 + 0,6t, де v – швидкість (м/с), t – температура (С), 331 м/с – швидкість поширення звуку при температурі 0С. Знайдіть з якою швидкістю поширюється звук у зимовий день з температурою  -15 і в літній день з температурою +30.

Для групи екологів:

Чисельність зубрів у заповіднику може бути знайдена за формулою: y = 50 +3t, де y – кількість особин, а t – час (у роках). Знайдіть скільки особин буде в даному заповіднику через 3 роки. Через скільки років у цьому заповіднику буде 65 зубрів?

Для групи біологів:

Волосся на голові в людини виростає приблизно зі швидкістю 0,04 см за добу. Через скільки днів довжина волосся в дівчинки досягне 50 см, якщо вважати, що їхня початкова довжина була 10 см. Якою буде довжина волосся в цієї дівчинки через 50 днів (формула l = 10 +0,04t, де l - довжина волосся в міліметрах, t - кількість днів).

Для групи працівників сільського господарства:

Перед тим як висадити рослини в теплицю необхідно довести t повітря в ній до 25.

Записати формулу залежності температура T (С)у теплиці в залежності від часу t (у хвилинах) нагрівання, якщо при нагріванні повітря в теплиці щохвилини  температура підвищувалася на 0,05, а початкова температура в теплиці була 6.

Заповнити таблиці:

Таблиця 1	t	12		Таблиця 3	t	10
	T		23		T		17
Таблиця 2	t	6		Таблиця 4	t	5
	T		14		T		20

Для групи медиків:

Медиками встановлено, що для нормального розвитку  дитина чи підлітка, якому х років, (х < 18) необхідно спати у годин на добу.

Задайте формулою залежність тривалості сну у (у годинах) від віку людини х (у роках), якщо відомо, що після народження дитина повинна спати не менш 17 годин на добу, зменшуючи тривалість сну на половину свого віку. (у = 17 – х/2)

Заповнити таблиці:

Таблиця 1	х	1		Таблиця 3	х	5
	у		9		у		11
Таблиця 2	х	3		Таблиця 4	х	7
	у		10		у		12

Для групи механізаторів:

Складіть формулу для обчислення витрати пального трактором при боронуванні поля, якщо на боронування 1га витрачається 2,5 кг пального. Заповніть таблицю.

Площа, га	3	25	43
Витрата пального, кг				1	15	20,5

 

(У задачі використовується функція y = kx (пряма пропорційність). Якщо m - витрата пального трактором, S - величина оброблюваної площі, то m = 2,5S)

Для групи туристів:

Турист проїхав від міста 10 км на автобусі, а потім йшов пішки, при цьому рухався рівномірно, продовжуючи рух у тому ж напрямку із швидкістю 4 км/год.

Записати формулу лінійної залежності всього пройденого шляху туристом S (у км) від часу руху туриста t (у годинах) (відповідь: S = 10 + 4t)

Заповнити таблиці:

Таблиця 1	t	0,5		Таблиця 3	t	1,5
	S		20		S		12
Таблиця 2	t	0,8		Таблиця 4	t	1,2
	S		15		S		18

Для групи проектувальників:

Складіть формулу для обчислення площі ділянки (мал. 2). Визначте вид функції.

Виконаєте наступні завдання:

• вкажіть реальну область визначення функції;
• знайдіть значення S при значенні аргументу a = 140 м.

(Площа ділянки S = 63a - 102*21. Функція лінійна, тому що формула має вид y = kx + b.)

 

 

 

 

 

 

 

 

 

 

Мал. 2.

Для групи технологів:

Конкретною моделлю функції y = kx + b є залежність калорійності молока від жирності, виражена формулою k = 113,5  a + 330, де k – калорійність молока в калоріях, a – відсоток жиру в молоці.

Виконаєте наступні завдання:

• вкажіть реальну область визначення функції;
• знайдіть значення k при значеннях аргументу a, що дорівнює  4%; 10%.

 

 

 

Для групи військових топографів:

Дві роти десантників, що атакують, наступають за законом: і
. Дайте відповідь на запитання: чи відбудеться зустріч наступаючих і де саме.

Слайд 9. Практична робота.

Кожен графік дає наочне зображення залежності між величинами, описує різні процеси. На практиці часто використовуються прилади для автоматичної реєстрації того чи іншого процесу. Ці прилади викреслюють графіки відповідних функціональних залежностей. Кожен вчений уміє не тільки «читати» побудовані приладами графіки, але і будувати ці графіки самостійно, без використання приладів. Пропоную кожному з вас «приміряти» на себе роль вчених і виконати дві практичні роботи. Одна робота покаже наскільки ви вміло, читаєте графіки, друга – як ви будуєте графіки залежностей.

Практична робота «Читання та складання графіків»

Практична робота для групи 1

Використовуючи графік залежності підвищення гемоглобіну від маси (г) вживання в їжу яблук або гранатового соку, відповісти на питання:

На скільки підніметься гемоглобін у крові в людини, що вживає в їжу 600 г  яблук чи 600 г гранатового соку?

Що позначає спільна точка графіків?

Зробити висновок про залежність гемоглобіну від маси уживаного в їжу продукту. Чи однакова ця залежність для яблук і для гранатового соку?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мал. 3.

Практична робота для групи 2

Використовуючи графік залежності маси M (г) рибки від маси корму m (г) відповісти на питання.

 Чи є функція M від m лінійної?

Яку масу буде мати рибка, що поїдає 15 г сухого корму, і рибка, що поїдає 15 г свіжого корму?

Зробити висновок про залежність M від m?  Чи однакова ця залежність для рибки на сухому кормі і рибки на свіжому кормі?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мал. 4.

Практична робота «Побудова графіків»

Практична робота для групи 3

Побудувати графік, що описує наступний процес: бак обсягом 12 літрів заповнили водою за п'ять хвилин, потім кран закрився, і через чотири хвилини з дна витягли пробку, бак виявився порожнім за три хвилини.

(результат роботи повинний виглядати так як на малюнку 5)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мал. 5.

 

Практична робота для групи 4

Побудувати графік, що описує наступний процес: у зимові місяці люди починають хворіти на грип, відсоток хворих людей досягає 70% на 10 день епідемії. Кількість хворих починає знижуватися на 20 день епідемії і вже на 30 день складає 10% населення.

(результат роботи повинний виглядати так як на малюнку 6)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мал. 6.

Результати роботи оформляються на великих аркушах, що потім вивішують на дошку. Діти роблять висновки.

Питання до висновків:

Зі скількох частин складається графік кожного процесу?

Що відбувається з функцією на першому етапі?

Що відбувається з функцією на другому етапі?

Що відбувається з функцією на третьому етапі?

Слайд 10. Додаткове завдання для визначення балу учнів за урок.

Накреслити графік функції

Слайд 11. Підведення підсумків.

Отже, у нас сьогодні був урок, на якому ви побачили застосування лінійної функції у різних сферах діяльності людини. Тому можна зробити висновок, що зусилля творців теорії функцій не були марними.

Учні відповідають на питання:

Що повторили і що закріпили?

Які завдання викликали труднощі?

Що сподобалося?

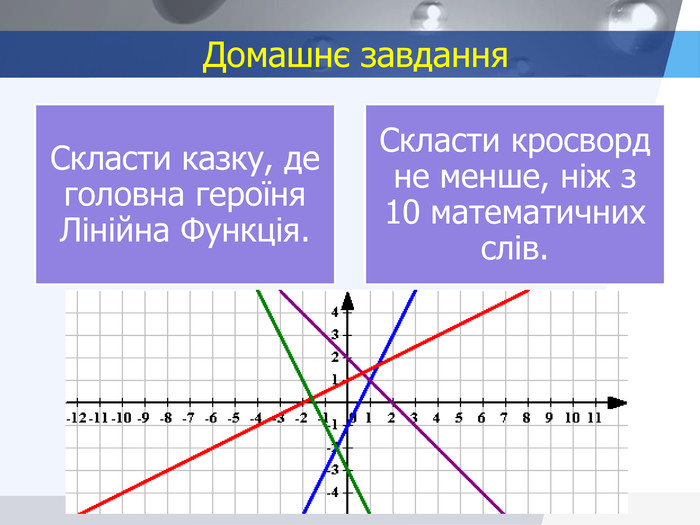
Слайд 12. Домашнє завдання.

• Скласти казку, де головна героїня Лінійна Функція.
• Скласти кросворд не менше, ніж з 10 математичних слів.

 

Слайд 13. Побажання.

«П р я м а  – є найкоротша відстань між двома точками,» – сказав Декарт.

І слідуючи цьому правилу, я закликаю вас у своєму розвитку іти по висхідній лінії, не зважаючи на втому, не обходячи труднощів, йти по прямій від точки незнання до точки знання.