Урок математики для 5 класу за темою "Прямокутний паралелепіпед. Куб. Піраміда"

Тема. Прямокутний паралелепіпед. Куб. Піраміда

Мета: ознайомити учнів із геометричними тілами, зокрема, прямокутним паралелепіпедом, кубом, пірамідою, які називаються многогранниками, розглянути елементи цих геометричних тіл, вчити обчислювати довжини ребер, суми площ, граней, кількості вершин, граней ребер піраміди, куба, прямокутного паралелепіпеда.

Тип уроку: урок засвоєння нових знань.

Обладнання: підручник, роздавальний матеріал.

Хід уроку

І. Організаційний етап

II. Перевірка домашнього завдання; актуалізація опорних знань

1. Вчитель пропонує учням розв’язання, за необхідності відповідає на запитання.
2. Математичний диктант

1) Довжина прямокутника дорівнює 12 см, а ширина — 5 см. Чому дорівнює площа прямокутника?

2) Сторона квадрата дорівнює 4 см. Чому дорівнює його площа?

3) Площа квадрата дорівнює 49 см². Чому дорівнює його сторона?

4) Периметр квадрата дорівнює 36 см. Чому дорівнює його сторона?

5) Прямокутник зі сторонами 3 см і 2 см поділили на квадрати зі стороною 1 см. Скільки утворилося квадратів?

6) Скільки потрібно квадратів зі стороною 3 см, щоб скласти прямокутник зі сторонами 9 см і 3 см?

3. Взаємоперевірка

1. 60 см²;  2. 16 см²;  3. 7 см;  4. 9 см;  5. 6 квадратів;  6. 3 квадрати.

III. Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності

Розглянемо моделі прямокутного паралелепіпеда, куба, піраміди, будь-якої призми. Як називають ці геометричні фігури? (Хто знає, той відповідає, демонструючи відповідну модель. У ході обговорення з’ясовує, що майже всі учні знають назви фігур, хіба що не знають назву призма.) Сьогодні ми детальніше вивчимо властивості цих геометричних фігур, які називаються геометричними тілами, а саме: прямокутного паралелепіпеда, куба, піраміди.

IV. Засвоєння нових знань

1. Приклади предметів, що дають уявлення про прямокутний паралелепіпед:

2. Елементи прямокутного паралелепіпеда: грані, ребра, вершини.

3. Виміри прямокутного паралелепіпеда.

4. Площа поверхні прямокутного паралелепіпеда.

5. Куб як окремий вид прямокутного паралелепіпеда.

6. Уявлення про піраміду.

7. Види пірамід.

8. Елементи піраміди: вершина, грані ребра, основа.

Лекція з елементами бесіди

Розгляньте модель прямокутного паралелепіпеда.

Оскільки з цим геометричним тілом учні вже знайомі, пропонується поставити це тіло нерухомо перед собою і зафіксувати: a — довжину, b — ширину, c — висоту, які є ребрами, що сходяться в одній вершині (не обов’язково довжина більша, ніж ширина чи висота).

Вершин 8, ребер 12, граней 6 (учні переконуються в цьому).

Учні отримують рис. 1–3 із зображеннями: 1) прямокутного паралелепіпеда; 2) куба; 3)піраміди.

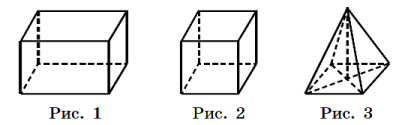
1. Прямокутний паралелепіпед.

Вчитель пояснює учням, як позначається прямокутний паралелепіпед (рис. 1).

Якщо a — довжина, b — ширина, c — висота, то сума довжин усіх ребер l = 4⋅(a + b + c).  Якщо відповісти на запитання, скільки потрібно паперу, щоб обклеїти даний паралелепіпед, то необхідно обчислити площу кожного прямокутника (грані); граней — 6, а саме: 3 пари рівних граней: верхнямі нижня основи, фронтальна (передня і задня) і профільна (ліва і права).

Під рис. 1 учні записують формули:

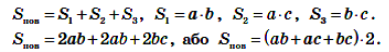
Виконання практичної роботи

Учитель роздає учням, так би мовити, одноразові моделі прямокутних паралелепіпедів — коробочки від ліків, зубної пасти тощо (можна заздалегідь запропонувати учням принести їх з дому). Учні переконуються, що їх грані — прямокутники, що не всі з них рівні між собою. Потім під керівництвом учителя учні розгортають ці коробочки (дістають розгортки прямокутного паралелепіпеда) і зафарбовують пари рівних граней однаковими кольорами. Далі складають коробку і переконуються: протилежні грані рівні (зафарбовані однаковим кольором).

Під керівництвом учителя учні доходять висновку: всі прямокутні паралелепіпеди мають 6 граней і 12 ребер, що у них усі грані — прямокутники (спільне). Відрізняються тим, що ці прямокутники мають різні розміри — виміри прямокутного паралелепіпеда.

2. Куб.

Учні розглядають куб і переконуються, що його ребра мають однакову довжину, грані — рівні квадрати, тобто мають однакову площу a² , а S _пов.кв. = 6 a²; сума довжин усіх ребер l = 12a.

На рис. 2 учні позначають куб і записують формули для куба.

Бажано продемонструвати кубик Рубіка.

Ку́бик Ру́біка (часто: кубик-рубік) — механічна головоломка, яку винайшов 1974 року угорський скульптор, винахідник Ерньо Рубік. Ерно Рубік назвав свій винахід «Магічний куб», але у 1980 році компанія  Ideal Toys перейменували головоломку за іменем винахідника і цього ж року виграла німецьку нагороду «Гра року» (Spiel des Jahres).

3. Піраміда.

Як приклад піраміди учитель демонструє пірамідку Рубіка

Пірамідка Мефферта (англ. Pyraminx), «Молдовська пірамідка» або «Японський тетраедр» — головоломка у формі правильної піраміди, подібна кубику Рубіка. Кожна грань піраміди поділена на 9 рівносторонніх трикутників. Завдання полягає в тому, щоб перевести пірамідку в конфігурацію з гранями однакового кольору. Іноді за схожість з кубічним аналогом називають також «Тетраедр Рубіка», хоча Ерне Рубік не має ніякого відношення до створення цієї головоломки.

На моделі піраміди та її зображенні вчитель показує: ^  бічні грані піраміди; ^ основу піраміди; ^  вершину піраміди; ^ бічні ребра піраміди; ^  ребра основи піраміди.

Потім учитель пояснює, як можна класифікувати піраміди. За можливості показує моделі різних видів пірамід (трикутної, чотирикутної тощо).

На рис. 3 учні позначають першою вершину піраміди, точку М  і основу ABCD.

Читається так: піраміда MABCD. MA, MB, MC, MD — бічні ребра, ABCD — ребра при основі AB, BC, CD, DA;

Кількість вершин, ребер, граней піраміди залежить від кількості сторін (кутів) многокутника, який лежить в основі піраміди.

• Єгипетські піраміди - архітектурні пам’ятки Стародавнього Єгипту, серед яких одне із Семи чудес світу - піраміда  Хеопса. Піраміди будувалися як грабниці для фараонів Стародавнього Єгипту.

• Приблизно в 120 кілометрах на південний схід від міста Меріда знаходяться руїни стародавнього міста Чичен-Іца. Це найвідоміша археологічна пам’ятка періоду Майя і держави Юкатана. В результаті розкопок на території міста було виявлено безліч архітектурних пам’ятників, зокрема, знамениті піраміди Чичен-Іци. Найбільшою серед них є Храм Кукулькана – піраміда з 9 ступенів висотою в 24 метри.

• Цікаво, що піраміди-усипальниці є і в Україні, на Полтавщині. Вони були збудовані під враженням від побачених пірамід у Єгипті. На зображенні нижче, зображено одну з таких пірамід, яка знаходиться в Березовій Рудці. Її вік - більше 100 років (1898-1899рр.). Висота піраміди - 9м. 

V. Первинне закріплення знань

Виконання  письмових вправ

[1]: №     (письмово).

VI. Підбиття підсумків уроку

1.Усне фронтальне опитування

1) Назвіть предмети навколишнього середовища, які мають форму:

а) прямокутного паралелепіпеда; б) куба; в) піраміди.

2) Якою геометричною фігурою є кожна з граней:

а) прямокутного паралелепіпеда; б) куба; в) піраміди?

3)Як називають прямокутний паралелепіпед, усі грані якого рівні?

2.Оцінювання учнів.

VII. Домашнє завдання

[1]: § 22 (усно); №     (письмово)