Урок "Многогранники"

Про матеріал

Матеріал для узагальнення теми "Многогранники". Формування компетентностей: *предметна компетентність:  узагальнити і систематизувати вивчений матеріал по темі “Многогранники’’, удосконалити вміння й навички у застосуванні цих знань при розв’язуванні задач. *ключові компетентності:  математична компетентність – розвивати логічне мислення, просторову уяву, формувати вміння вирішувати проблемні ситуації, показати зв'язок математики з життям.  уміння вчитися впродовж життя – аналізувати, контролювати, корегувати та оцінювати результати своєї навчальної діяльності.  соціальна та громадська компетентності – продовжити виховання в здобувачів освіти шанобливого ставлення один до одного, почуття товариства, культури спілкування, почуття відповідальності, виховувати культуру ділового спілкування.  спілкування державною мовою – грамотно висловлюватися рідною мовою, доречно та коректно вживати в мовленні математичну термінологію.

Перегляд файлу

Овруцький професійний ліцей

Методична розробка уроку з математики на тему:

$C:\Users\Admin\Desktop\IMG_0079.JPG$

викладача математики

Король Людмили Миколаївни

2021 р.

Тема: Многогранники.

Формування компетентностей:

*предметна компетентність:

узагальнити і систематизувати вивчений матеріал по темі “Многогранники’’, удосконалити вміння й навички у застосуванні цих знань при розв’язуванні задач.

*ключові компетентності:

математична компетентність – розвивати логічне мислення, просторову уяву, формувати вміння вирішувати проблемні ситуації, показати зв'язок математики з життям.
уміння вчитися впродовж життя – аналізувати, контролювати, корегувати та оцінювати результати своєї навчальної діяльності.
соціальна та громадська компетентності – продовжити виховання в здобувачів освіти шанобливого ставлення один до одного, почуття товариства, культури спілкування, почуття відповідальності, виховувати культуру ділового спілкування.
спілкування державною мовою – грамотно висловлюватися рідною мовою, доречно та коректно вживати в мовленні математичну термінологію.

Обладнання: моделі многогранників, опорні конспекти, зображення многогранників.

Тип уроку: урок узагальнення і систематизації знань.

Форма проведення: урок з ігровими моментами.

Хід уроку.

І. Організаційний момент.

Інтерактивна вправа: гра «Пароль» (Вхід на урок – назва будь-якого терміну з вивченої теми)

ІІ. Актуалізація опорних знань.

(Кросворд проектується на дошку і кожному на аркуші паперу на парту) (5 хв.)

Кросворд

		1
			2
			3
				4
		5
6
			7
		8
	9
10
			11
				12

Многогранник, який складається з плоского многокутника, точки, яка не лежить у площині основи і всіх відрізків, що сполучають вершину з точками основи.(піраміда)
Два плоскі многокутники, з яких складається призма. (основа)
Висота бічної грані правильної піраміди, проведена з її вершини.(апофема)
Півплощини, які утворюють двогранний кут. (грань)
Сторона граней многокутника. (ребро)
Основа паралелепіпеда. (паралелограм)
Призма, основою якої є паралелограм. (паралелепіпед)
Правильна трикутна піраміда. (тетраедр)
Відрізок, який сполучає дві вершини призми, що не належать одній грані. (діагональ)
Основа прямокутного паралелепіпеда. (прямокутник)
Многогранник, який складається з двох плоских многокутників, що лежать у різних площинах і суміщаються різних площинах і суміщають паралельним перенесенням, та всіх відрізків, що сполучають відповідні цих многокутників. (Призма)
Правильний многогранник, в якого всі грані квадрати. (Куб)

ІІІ. Узагальнення і систематизація знань.

Інтерактивна вправа «Мозковий штурм».

Запитання (на швидкість) ( можна сказати, показати на малюнку, моделі) ( 5 хв ).

Що таке призма?
Що таке основа призми?
Висота призми.
Діагональ призми.
Бічна поверхня призми.
Повна поверхня призми.
Пряма призма.
Правильна призма.
Піраміда.
Бічні ребра піраміди.
Висота піраміди.
Бічні грані якої форми?
Зрізана піраміда.
Бічні грані зрізаної піраміди.
Правильна піраміда.
Бічна поверхня піраміди.
Повна поверхня піраміди.
Паралелепіпед
Куб
Лінійні розміри прямокутного паралелепіпеда.

Розв’язування задач ( запис на дошці ) ( 25хв ).

1) Площа основи правильної чотирикутної призми 25см, а її бічне ребро 10см. Знайти S бічної поверхні.

2) Сторони основи прямокутного паралелепіпеда дорівнюють 2 і 3см, а бічне ребро 6см. Знайти діагональ паралелепіпеда.

3) Знайти площу повної поверхні правильної чотирикутної піраміди, сторона основи якої 4см, апофема 9см.

4) Бічне ребро правильної піраміди нахилене до площини основи під кутом β. Відстань від основи висоти піраміди до бічного ребра = d. Знайти бічне ребро.

5) Через сторону нижньої основи правильної трикутної призми і протилежну їй вершину верхньої основи проведено переріз, який утворює з площиною основи кут β. Перерізом є трикутник з кутом ԃ при вершині верхньої основи. Висота призми Н. Знайти площу перерізу.

Емпатійний твір ( 4хв.).

Перед проведенням даного уроку заздалегідь декільком учням було дано завдання написати емпатійний твір про будь – який многогранник.

Наприклад:

Твір: «Я – призма».

Моє ім’я Призма. Я належу до великої родини многогранників, але маю ряд особливостей, якими вирізняюсь з – поміж інших.

У мене є: основи, які …

Відрізки, які …

Моя поверхня складається з …

Бічні грані мають форму …

Я можу бути прямою, якщо …

Правильною якщо …

Твір: «Я – парлелопіпед».

Я рідний брат призми. Моїми основами є паралелограми. Мої грані, які не мають сліпих вершин, називаються протилежними. Вони паралельні і рівні. Мої діагоналі перетинаються в одній точці і діляться нею навпіл. Ця точка є моїм центром симетрії. В моїй основі може лежати прямокутник. Тоді всі грані будуть прямокутниками. Для виділення цієї властивості в такому випадку називайте називайте мене прямокутним, а мого брата, в якого всі ребра рівні – кубом.

Твір: «Я – піраміда».

Я особливий многогранник, в мене лише одна основа. Для того щоб створити мене, крім основи, вам буде необхідна ще точка, яка не лежить в площині основи. Ця точка буде моєю вершиною. Відрізки, які сполучають мою вершину з вершинами основи, називають бічними ребрами. Мої бічні грані утворюються трикутниками. В мене э дві рідні сестри. Це зрізана піраміда, бічними гранями якої є трапеція, а основами – подібні многокутники і правильна піраміда, основою якої є правильна піраміда, основою якого є правильний многокутник, а основа висоти збігається з центром цього многокутника

І тому подібне. ( можна зробити гарне сатиричне зображення). (4 – 5хв).

Зробимо невеликий екскурс в історію.

Викладач задає запитання і декілька варіантів відповідей, 30 секунд на обдумування, і якщо відповіді немає, він сам говорить учням вірну відповідь.

Завдання для зонального розвитку, самоосвіти, ерудованості. (роздрукувати кожне запитання на окремому листкові, запитання і відповіді проектуються на дошку).

1) Хто з великих математиків запропонував першим метод нумерації крісел по рядах і місцях?

а) Ньютон.

б) Декарт.

в) Лейбніц.

г) Гаусс.

2) Більшість вчених – це стародавні греки, але один з цих іншої національності. Хто?

а) Архімед.

б) Гаусс.

в) Піфагор.

г) Фалес.

3) Хто з цих вчених – математиків загинув на дуелі?

а) Вієт.

б) Лейбніц.

в) Абель.

г) Галуа.

4) Хто була перша жінка – математик?

а) Софі Жермен.

б) Софія Ковалевська.

в) Гортензія Лепот.

г) Генатія Александрійська.

5) У якій країні дроби називали “ламаними числами”?

а) Стародавня Русь.

б) Німеччина.

в) Англія.

г) Стародавня Греція.

6) Ім’ям якого вченого називається геометрія, яка вивчається в школі?

а) Піфагор.

б) Євклід.

в) Архімед.

г) Ньютон.

Відпочинемо. (3 хв).

Задача – жарт. Два козаки часто сперечалися, хто кого обжене на коні. Перемагав то один, то другий, їм це набридло і тоді один запропонував інший спір: нехай переможе той, чий кінь дістанеться призначеного місця другим. Козаки стали на старт, їм дали команду рушати, але жоден з них не зрушив з місця. Глядачі посміялися і вирішили, що такий спір неможливий, оскільки можна стояти скільки завгодно. Але ось до козаків підійшов один дідусь і щось їм прошепотів, і за хвилину ті вже стрімголов мчали вперед, намагаючись випередити один одного. Що ж їм сказав дідусь, якщо умови спору не змінилися: виграє той, чий кінь прийде другим?

(пересядьте).

Додаткова інформація.

1) Теорема Ейлера.

Вправа1. Підрахувати число вершин, граней і ребер деяких моделей багатогранників: трикутної і чотирикутної пірамід, трикутної і чотирикутної призм. Потім занести ці дані в таблицю. (поставити на столи моделі та роздати таблиці для заповнення)

Назва багатогранника	В	Г	Р
Трикутна піраміда	4	4	6
Чотирикутна піраміда	5	5	8
Трикутна призма	6	5	9

2) Правильні многокутники - це багатокутники, у яких всі сторони і всі кути рівні, правильні багатогранники - це опуклий многогранник, гранями якого є рівні між собою правильні многокутники і в кожній з його вершин сходиться однакова кількість ребер. Назва "правильні" йде від античних часів, коли прагнули знайти гармонію, правильність, досконалість в природі і людині. До цих пір багатокутники нерідко називають у науці по-грецьки з закінченням "гон": полігон - багатокутник,

як приклад Пентагон (від грец. Πεντάγωνον - «п'ятикутник») - назва будівлі Міністерства оборони США, що має форму правильного п'ятикутника, знаходиться в штаті Вірджинія недалеко від Вашингтона.

3) Кожен з вас знайомий з найпростішими просторовими математичними фігурами, або многогранниками. По-грецьки вони закінчуються на "едр".

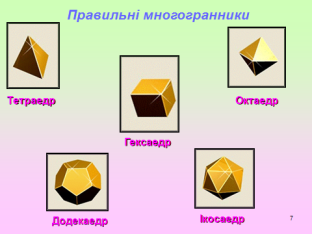
Всі правильні багатогранники були відомі ще у Стародавній Греції, і їм присвячена заключна, 13-а книга знаменитих "Начал" Евкліда. Ці багатогранники часто називають також Платоновими тілами - в ідеалістичної картині світу, даної великим давньогрецьким мислителем Платоном, чотири з них уособлювали 4 стихії: тетраедр - вогонь, куб - землю, ікосаедр - воду, октаедр - повітря, п'ятий же багатогранник, додекаедр, символізував світобудову - його по-латині стали називати quinta essentia (квінта есенція), що означає все найголовніше, основне, істинну сутність чого-небудь.

Крім правильних многогранників, є напівправильні многогранники. Тринадцять вперше відкрив і описав Архімед - це тіла Архімеда. Вони відрізняються від Платонових тіл тим, що їх грані - правильні багатокутники декількох типів.