Урок "Множини та операції над ними"

   Мета. Ввести поняття множини, елементів множини, підмножини, визначити дії над множинами, навчити учнів записувати множини, знаходити переріз, об’єднання та різницю множин.

   Тип уроку. формування вмінь і навичок.

Хід уроку

1. Організаційна частина.

Повідомляю тему, мету уроку.

2. Актуалізація опорних знань.

— Зіронька! Красуня! Лиска! — підганяє па­стух корів, що йдуть на пасовисько. Так і ди­вись, якась поверне до лісу або загубиться. Особ­ливо Красуня: тільки замислився — шукай вітру в полі. Зіронька — та нічого: поки батогом не підженеш, з місця не зсунеться. А з Лискою своя біда: дуже бодлива, не підчепила б когось на роги...

Для пастуха кожна корова — особлива: у кож­ної свій характер, свої звички. Для дaчникiв усі корови на галявині однакові — просто стадо.

Ось що означає точка зору. Для одного — неповторні індивідуальності. Для іншого — су­купність, що розглядається як єдине ціле.

Взагалі, людині властиво розглядати те або інше зібрання предметів, споріднених за якою-не-будь ознакою, як самостійний об'єкт.

Перша скрипка, друга скрипка, альт, віолон­чель, контрабас, флейта, гобой, фагот, валтор­на, труба, литаври. Про все це, взяте разом, ми говоримо: оркестр.

Посуд для кави, молока, цукру, кілька ча­шок і стільки ж блюдець. А все це разом — сервіз.

А, Б. В. Г. Д..Ю, Я. Всі літери разом —алфавіт.

1,2,3.4,5.6, 7,8,9. 10, 11, 12,... Разом усі ці числа утворюють натуральний ряд чисел.

Невипадково кожну з них сукупностей ми називаємо іменниками в однині: оркестр, сервіз, алфавіт, ряд — ідея об'єднання помітна навіть у такій граматичній категорії.

Подібне об'єднання доцільне, коли треба гово­рити про сукупність об'єктів як про єдине ціле.

Німецький математик Георг Кантор (1845— 1918), коли йому було 30 років, дocлiджyючи тригонометричні ряди і числові послідовності, опинився перед необхідністю порівнювати між собою нескінченні сукупності чиceл. Для розв'язування проблем, що постали при ньому. Кантор увів поняття множини, відповідно роз­винув це поняття і став одним із засновників теорії множин.

Ця нова теорія стала наріжним каменем усієї математичної науки. Основні ідеї, символи цієї теорії допоможуть нам обговорювати певні ма­тематичні проблеми, виконувати записи, роби­ти пояснення конкретнішими, значно коротши­ми і простішими.

у сучасній математиці поняття множини вва­жається одним з основних. Так або інакше з нього починається викладання традиційних матема­тичних дисциплін і побудова нових математич­них теорій, що виникають у зв'язку з поширен­ням сфери застосування математики. Універ­сальність цього поняття полягає в тому, що під нього можна підвести будь-яку сукупність як матеріальних, так і нематеріальних об'єктів. Тут підійде все: марки, люди, зірки, птахи, квіти, корови, книжки, числа, точки, функції, аксіо­ми, відтінки, типи людських характерів, війни, революції тощо.

Навіть самі множини можуть об'єднуватись у множини. Наприклад, математики говорять про множину фігур на площині, про множину тіл у просторі, але кожну фігуру, кожне тіло вони розглядають як множину точок.

Що ж таке множина? Що ж це за об'єкт розгляду, в якому, як у скриньці фокусника, хова­ються і марки, і числа, і посуд, і музичні інстру­менти?

Г. Кантор говорив: «Під множиною розумі­ють об'єднання в одне спільне об'єктів, які добре розрізнює ваша інтуїція або наша думка».

Але ці слова не можна розглядати як строге математичне означення множини. Такого озна­чення не існує, оскільки поняття множини є в математиці первинним, а на його основі базу­ються інші математичні поняття.

Отже, множина — це основне математичне поняття, і не означається.

У повсякденному житті зміст цього поняття можна виразити словами: сукупність, набір, клас, табун, колекція, команда, екіпаж, букет, зграя тощо.

Наведемо приклади різних множин і підбе­ремо інші слова, що вказують на ту саму су­купність об'єктів. Множина квітів у вазі — бу­кет. Множина сухих листочків різних рослин у альбомі — гербарій. Множина книжок на поли­цях — бібліотека. Множина людей, які є грома­дянами однієї країни. — співвітчизники.

Поняття множини використовують у різних шкільних предметах: математиці, географії, біо­логії, хімії. Наведемо приклади.

Коло — це множина всіх точок площини, рівновіддалених від однієї точки цієї площини. Меридіан — це множина всіх точок земної по­верхні, що мають одну й ту саму довготу. Пара­лель — це множина всіх точок земної поверхні, що мають одну й ту саму широту. Ізотерма — це множина всіх точок земної поверхні, що ма­ють однакову середню річну температуру. Бджо­лина сім'я (рій) — це множина бджіл.

Множина подібних організмів, які мають однакову будову та функції, є вид. Множина видів є рід. Множина родів — родина. Множи­на родин — загін. Множина загонів — клас. Множина класів — тип. Обмін речовин — це множина хімічних реакцій. Кухонна сіль — це множина молекул NaCl.

3. Множини. Елементи множин. Позначення множин.                               Запис елементів множин. Операції  над множинами.

• Під множиною в математиці розуміють зібрання, сукупність будь-яких предметів, об'єднаних між собою деякою загальною для них усіх ознакою.

Прикладом множин можуть бути множина учнів класу, множина книг у бібліотеці, множина цифр, множина чотирикутників, множина коренів рівняння тощо.

•    Предмети (об'єкти), з яких складаються множини називаються їх елементами.

• Множини позначають великими літерами латинського алфавіту (A, B, X, Y, M, N  тощо), а елементи множин малими літерами ( a, b, x, y, m, n   тощо) .

• Належність елемента  а  множині  А позначається символом 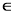.    Наприклад .

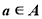Якщо елемент b не належить множині А то записують .

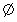•     Множину, яка не має жодного елемента називають порожньою і позначають         .

         Н а п р и к л а д, множина точок перетину двох паралельних прямих є порожньою.

• Множина В називається підмножиною множини А,

     якщо кожний елемент множини В належить множині А. 

      Позначається: .

Н а п р и к л а д. Нехай  -

множина всіх цифр, а -  множина парних цифр.

 Тоді   .

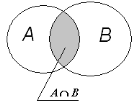•   Перерізом множин А і В називається множина , яка складається

                                              з усіх елементів, які належать кожній з даних множин.

                                             Позначається: .

                                              Н а п р и к л а д. Якщо ,  ,

                                               то .

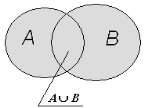
•        Об'єднанням множин А і В називається множина, яка складається

        з усіх елементів, які містяться хоча б в одній з двох множин

        А і В і тільки з них.

        Позначається: .

        Н а п р и к л а д. Якщо ,  ,

                                      то .

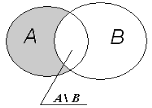•     Різницею множин А і В називається множина всіх таких

                                                             елементів множини А, які не містяться у множині В.

                                                             Позначається: .

                                                             Н а п р и к л а д. Якщо ,  ,

                                                              то ;  .

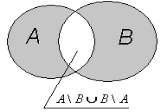
•    Симетричною різницею множин А і В  називається

       множина .

         Н а п р и к л а д. Якщо ,  ,

                                      то = .

4. Вироблення вмінь і навичок. (розв’язування завдань вправи 32)

1. Нехай А – множина коренів рівняння   . Які з поданих записів вірні?

 а) ;       б) ;       в) ;        г) .

  2. Записати множини різними літерами, перелічивши їх елементи :

  а) додатні числа, кратні 7 і менші від 60 ;

  в) множину коренів рівняння ;

  д) множину простих чисел, менших 40 ;

  е) множину учнів класу, які зараз відсутні .

  3.  Записати всі підмножини множини

      5. Знайти об'єднання і переріз множин розв'язків рівнянь :

      а)   і   ;        б) і  .

      7.  Дано   ,  і  .  Знайдіть:

    а) ;     б) ;      в) ;    г) ;    д) ;    е) ;  є) .

     5.  Підсумок уроку.

          Сьогодні на уроці ми вивчили поняття множини, навчились записувати множини, виконувати операції над множинами.

     6.  Домашнє завдання.      Стор 92 – 93,  § 5.2.  вправа 32 ( 2(б,г), 3, 6, 9)