Урок на тему «Додавання і віднімання звичайних дробів з однаковими знаменниками».
У розробці представлений урок з теми «Додавання і віднімання звичайних дробів з однаковими знаменниками». Урок такого плану підготовлений в системі, для досягнення оптимального результату. Пропонована організація уроку забезпечує роботу всіх каналів сприйняття, освітня діяльність спрямована на підвищення результативності, сприяє розвитку потенціалу кожної дитини, розкриття закладених в ньому можливостей. Учні можуть міркувати і робити висновки; слухати співрозмовника і вести діалог; працювати в парі і групі; викладати і аргументувати свою точку зору; оцінювати себе і товаришів.

![]()
Додавання і віднімання звичайних дробів з однаковими знаменниками.
(Узагальнення і систематизація знань, умінь і навичок)
Сергевніна Наталя Євгенівна
Вчитель І кваліфікаційної категорії
ЗЗШ №52
м. Запоріжжя
2021 р.
5 клас.
Урок математики.
Тема. (Слайд 1)
Додавання і віднімання звичайних дробів з однаковими знаменниками.
Мета. (Слайд 2)
Узагальнити та систематизувати знання учнів щодо додавання і віднімання дробів з однаковими знаменниками; розвивати математичну мову, логічне мислення учнів; формувати пізнавальну компетентність; виховувати інтерес до математики, працьовитість, активність, цілеспрямованість, наполегливість, виховувати старанність, культуру спілкування та відповідальність, вміння співпрацювати з однокласниками.
Учень повинен знати:
- Означення звичайного дробу.
- Які існують види дробових чисел.
- Як порівнюються звичайні дроби.
- Як додаються та віднімаються звичайні дроби з однаковими знаменниками.
- Як перетворити неправильний дріб у мішане число та навпаки.
Нормувати:
- знання і вміння додавати звичайні дроби;
- знання і вміння порівнювати звичайні дроби;
- знання і вміння перетворювати дробові числа.
Цінувати:
- уміння долати труднощі;
- прагнення досягти мети.
Тип уроку. (Слайд 3)
Узагальнення і систематизація знань, умінь і навичок.
Хід уроку
I. Організаційний момент
II. Актуалізація опорних знань
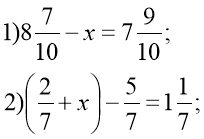 III. Розв'язання задач
III. Розв'язання задач
ІV. Рефлексія.
V. Домашнє завдання
І. Організаційний момент.
1. Сьогодні ми на уроці будемо розв’язувати різноманітні задачі на звичайні дроби,подібне ми вже робили,тому ви легко справитесь з завданнями.
Отже, ми починаємо урок, а на уроці ми…
Уважні. Активні. Розумні. Організовані. Кмітливі. Працьовиті.
2. Мотивація. (Слайд 4)
Адже, як сказав великий мислитель Цицерон:
«Без знання дробів ніхто не може визнавати, що знає математику».
А скажіть будь ласка де нам ще потрібні дроби крім математики?
(Слайд 5)
Насправді поняття дробу використовується практично в усіх сферах життя. Навіщо дитині, що захоплюється живописом, розуміти дроби? Теорія лінійної перспективи - предмет зменшується в постійне число разів залежно від відстані від спостерігача. Поняття дробового числа допоможе точніше розуміти і бачити пропорції предметів, які хочеться зображувати. У середній школі вивчають основи фізики, хімії, географії. Частіше за усе завдання по цих предметах включають математичні розрахунки: порахувати відсотковий вміст кислоти в розчині, підставити дані у формулу і знайти невідому величину. Долі і частини ми зустрічаємо майже щодня: це і відсоток по вкладу у банку, і знижки. Математика п'ятого і шостого класів - основа фінансової грамотності і аналізу в повсякденному і професійному житті.
Тарас Шевченко із 47 років життя 10 був у засланні, (Слайд 6)
24 роки – кріпаком і лише 13 років – на волі.
Задача. Порахувати, яку частину свого життя Т.Г.Шевченко провів на волі,у засланні.у кріпацтві.
А які знання ми з вами зараз застосували?
Знання про звичайні дроби. Я думаю, що ви ще раз переконалися, що знати все про звичайні дроби дуже корисно.
II. Актуалізація опорних знань.
- Перевірка домашнього завдання. Два учні працюють біля дошки;
- Клас грає "Мікрофон". (Слайд 7)
III. Розв'язання задач
- «Знайдіть помилку» (Слайд 8)
-
2)
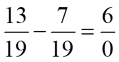 3)
3) 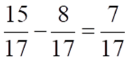
4) 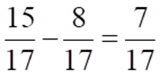 5)
5) 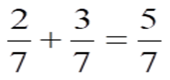
- Розв’язати рівняння (Слайд 9)
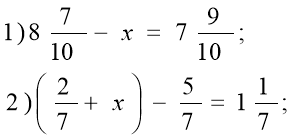
3. Гра «Магічний квадрат». Усно (Слайд 10)
4. Гра «Магічний квадрат» письмово у зошиті (Слайд 11)
Візьміть олівці і перевірте відповіді. Підніміть руки у кого немає помилок.
Фізкультхвилинка . (Слайд 12)
5. Розв'язання задач по групам (Слайди 13 – 14)
І група – задача № 1
Скільки років було Т. Г. Шевченко, коли вийшла його збірка поезій, яка поклала початок новому періоду в історії української літератури, якщо дріб ![]() цього числа дорівнює 6.
цього числа дорівнює 6.
ІІ група – задача № 2
У скільки років Т. Г. Шевченко став кріпаком?
Знайди ![]() від числа 70.
від числа 70.
ІІІ група – задача № 3
Скільки всього віршів та поем написав Т. Г. Шевченко
на української мові, якщо ![]() цього числа дорівнює 47.
цього числа дорівнює 47.
6. Розв'язання задачі усім класом. (Слайди 15 – 17)
Задача. Подорожуючи на човні по Дніпру, Барвінок за перший день проплив 72 км, за другий день - ![]() , того що проплив за перший день, а за третій -
, того що проплив за перший день, а за третій - ![]() того, що за другий. На скільки кілометрів менше проплив Барвінок за третій день, ніж за другий?
того, що за другий. На скільки кілометрів менше проплив Барвінок за третій день, ніж за другий?
7. Інтелектуальна розминка (Слайди 18 – 19)
8. Самостійна робота (Слайд 20)
І варіант
1. Порівняйте дробові числа:
1) ![]() і
і ![]() ; 2)
; 2) ![]() і
і ![]() ; 3)
; 3) ![]() і
і ![]() .
.
2) Перетворіть неправильний дріб у мішане число.
![]()
3) Довжина дороги 20 км. Заасфальтували ![]() дороги.
дороги.
Скільки кілометрів дороги заасфальтували? Скільки залишилося заасфальтувати?
ІІ варіант
1. Порівняйте дробові числа:
1) ![]() і
і ![]() ; 2)
; 2) ![]() і
і ![]() ; 3)
; 3) ![]() і
і ![]() .
.
2) Перетворіть неправильний дріб у мішане число.
![]()
3) Купили 5 кг 600 г цукру і витратили на варення всього ![]() цукру. Скільки цукру пішло на варення?
цукру. Скільки цукру пішло на варення?
Скільки цукру залишилося?
ІV. Рефлексія. (Слайд 21)
Що вам найбільше сподобалося на сьогоднішньому уроці?
- На уроці я…
- Дізнався…
- Навчився…
- Зрозумів…
- Не вмів, а тепер умію…
Діти, як ви думаєте: що важливіше – Що ви про себе думаєте чи що про вас думають інші люди?
Один з відомих письменників сказав, що людину можна оцінювати дробом, чисельник якого становить те хороше, що вона думає про себе сама, а знаменник те хороше, що про цю людину думають інші. То ж бажаю вам щоб дріб у кожного з вас був завжди правильним.
V. Домашнє завдання (Слайд 22)
§Повторити §§ 28 – 29
Розв’язати №793, №795.
Додатково розв’язати № 797.


про публікацію авторської розробки
Додати розробку
