Урок на тему: "Квадрат двочлена"
Тема. Квадрат двочлена.
Мета уроку: Домогтися розуміння і засвоєння змісту формул «квадрат суми двох
виразів» та «квадрат різниці двох виразів», формувати вміння застосовувати
ці формули до перетворення квадрата двочлена в многочлен стандартного вигляду; розвивати навички самоконтролю, творче мислення, культуру математичного мовлення й записів; виховувати зацікавленість у пізнанні нового.
Очікувані результати: Учні повинні знати формули квадрата суми і квадрата різниці двох виразів,вміти застосовувати їх до перетворення виразів.
Обладнання: підручник, роздавальні матеріали, презентація.
Тип уроку: засвоєння нових знань і вмінь.
Хід уроку
І. Організаційний етап.
ІІ. Перевірка домашнього завдання.
Самоперевірка за готовими розв’язками.
Декілька учнів записують на дошці розв’язання вправ домашнього завдання, решта здійснюють самоперевірку й беруть участь в обговоренні розв’язань.
ІІІ. Актуалізація опорних знань. робота в групах.
Гра «Шифрувальник».
- Нам потрібно розшифрувати вислів Софії Ковалевської.
Група А розшифровує перше слово, група В- друге слово, група С – третє слово.
|
у |
м |
а |
т |
е |
м |
а |
т |
и |
к |
і |
в |
і |
с |
н |
у |
є |
с |
в |
о |
я |
м |
о |
в |
а |
- |
ц |
е |
ф |
о |
р |
м |
у |
л |
и |
Група А ( розшифровує перше слово вислову)
|
Вирази |
(3α2 b)2 |
2α ·3b2 α |
(- 4 с)2 |
2·4х·5у |
(9 х3 у)2 |
|
Відповіді |
|
|
|
|
|
|
Букви |
|
|
|
|
|
Ключ до шифру подано в таблиці
|
Букви |
ТЕ |
ТИ |
МА |
КА |
МА |
|
Відповіді |
6α2 b2 |
40ху |
9 α4 b2 |
81х6 у2 |
16 с2 |
Група В ( розшифровує друге слово вислову)
|
Вирази |
(5с)2 |
2b ·3b2 α |
(- 0,4 с)2 |
2·4х·(-3)у |
(6 х4 у)2 |
|
Відповіді |
|
|
|
|
|
|
Букви |
|
|
|
|
|
Ключ до шифру подано в таблиці
|
Букви |
Н |
І |
Є |
С |
У |
|
Відповіді |
0,16 с2 |
25 с2 |
36х8 у2 |
6αb3 |
-24ху |
Група С ( розшифровує третє слово вислову)
|
Вирази |
(-2с)2 |
2х2 ·3х2 у |
(- 0,3с3)2 |
2·4у·(-3)у2 |
(5 х2 у5)2 |
|
Відповіді |
|
|
|
|
|
|
Букви |
|
|
|
|
|
Ключ до шифру подано в таблиці
|
Букви |
М |
Р |
ЛИ |
У |
ФО |
|
Відповіді |
0,09с6 |
6х4 у |
25х4 у10 |
-24у3 |
4с2 |
Із завданням справились і вислів розшифрували:
У математиків існує своя мова - це формули.
ІV. Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності.
Розповідь учителя. Відомий угорський, швейцарський і американський математик Дьордь Пойа писав: «Найкращий спосіб вивчити що-небудь — це відкрити самому». Сьогодні ми «відкриємо» важливі формули, які належать до формул скороченого множення, а саме квадрат суми двох виразів і квадрат різниці двох виразів. Ми вміємо знаходити добуток двох многочленів. А тепер давайте будемо експериментувати: розглянемо випадок, якщо ці многочлени рівні.
V. Сприйняття та усвідомлення нового матеріалу.
1. Виведення формули квадрата суми і квадрата різниці.
Знайдемо добуток двох многочленів, кожний із яких дорівнює:
а) a+ b ; б) a - b .
Розв’язання:
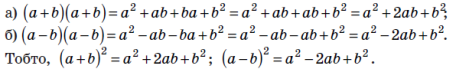
У ці формули замість a і b можна підставляти будь-які вирази: одночлени або многочлени.
2. А зараз пригадаємо як обчислити площу квадрата та прямокутника.
Перевіримо ваші математичні здібності .
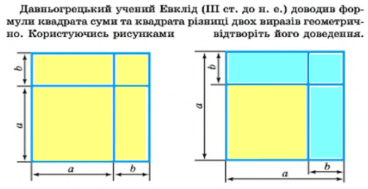
Ми вивели формулу квадрата суми двох виразів:
(α + b)2 = α2 + 2αb + b2
Словесне формулювання формули квадрата суми двох виразів:
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів плюс квадрат другого виразу.
та формулу квадрата різниці двох виразів:
(α - b)2 = α2 - 2αb + b2
Словесне формулювання формули квадрата різниці двох виразів
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток цих виразів плюс квадрат другого виразу.
Щоб краще запам’ятати цю формулу складемо для неї шифр:
![]()
![]()
![]()
![]()
![]()
![]() ( + )2 = 2 + 2 + 2
( + )2 = 2 + 2 + 2
3. Колективне виконання завдань під керівництвом учителя.
1. Застосуйте формули квадрата двочлена:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2. Виконайте піднесення до квадрата:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) 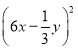 ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
VІ. Осмислення нового матеріалу.
Робота в парах.
1. Чи є тотожністю рівність:
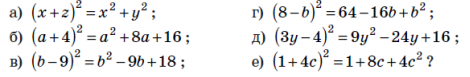
Якщо рівність не є тотожністю, змініть її так, щоб вона стала тотожністю.
2.Замініть зірочки одночленами так, щоб утворилася правильна рівність:
![]() ;
; ![]() ; (* + в)2 =* + 4ав +*2.
; (* + в)2 =* + 4ав +*2.
Робота в групах.
1. Подайте у вигляді многочлена вираз:
1 група 2 група 3 група
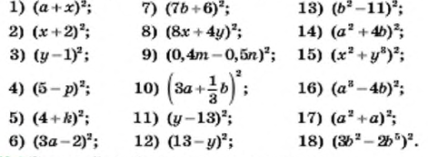
1) ![]() ; 3)
; 3) ![]() ; 5)
; 5) ![]() ;
;
2) ![]() ; 4)
; 4) ![]() ; 6)
; 6) ![]() .
.
3. Кожна група отримує завдання, як швидко порахувати, використовуючи вивчену формулу:
312 = 212 = 412 =
VІІ. Підсумок уроку. З якою формулою познайомилися на уроці?Сформулюйте її.
VІІІ. Домашнє завдання.
1
-
Супер!!!


про публікацію авторської розробки
Додати розробку
