Урок на тему: "Сума перших n членів арифметичної прогресії"

Конспект уроку з алгебри, 9 клас

Тема уроку. Сума перших n членів арифметичної прогресії

Мета уроку:домогтися засвоєння учнями формул суми перших n членів арифметичної прогресії через перший і n-й члени та через перший член і різницю арифметичної прогресії. Виробити вміння: записувати вивчені формули залежно від умови задач, а також використовувати їх для розв'язування за­дач, що передбачають обчислення суми перших п членів арифметичної прогресії. Підприємливість і фінансову грамотність.

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання: опорний конспект по темі «Арифметична прогресія», роздавальний ма­теріал (картки для роботи в групах), презентація.

Використана література: Д.В. Васильєва, Н.І. Василюк [збірник задач з математики

                                               «Наскрізні лінії компетентностей та їх реалізація ». – 

                                                 Освіта, 2017 р.]; О.С. Істер [ підручник з алгебри 9 кл. –

                                                 Генеза, 2017 р. ]

Хід уроку

I. Організаційний етап

Перевірка  готовністі  учнів до уроку, налаштування  їх на роботу.

II. Перевірка домашнього завдання

Встановити відповідність за допомогою стрілочок між завданням та відповіддю до нього (на дошці заготовлений рисунок).

III. Актуалізація опорних знань та вмінь учнів

      На минулому уроці ми з вами ознайомилися з арифметичною прогресією і формулою для обчислення її n- ного члена. Запишіть на дошці формулу.(учні записують на дошці формулу і пояснюють її складові: a1  і  d).

А зараз ми повторимо раніше вивчене.

Усні вправи ( міні - презентація)

1. Чи є послідовність арифметичною прогресією. Якщо так, то назвати її перший член та різницю.

а) 2; 5; 8; 11; 14… (так, a1 =2,  d = 3)

б) 4; 8; 16; 32; 64… ( ні )

в) 1;2; 3; 4; 5… (так, а1 =1, d=1)

    2. Знайти а6 і а10 для послідовності аn, якщо а1=4, d=2.

    3. Відомо, що в скінченній арифметичній прогресії сума першого й останнього 

        членів дорівнює 10. Чому дорівнює сума другого і передостаннього членів?

IV.  Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів

   Задача  (умова написана на дошці)

Задана числова послідовність: 1; 2; 3; 4; 5; 6…

Знайти суму перших  5-ти, 8-ми, 12-ти  її членів (15, 36, 78, )

А ста членів ? Як ви думаєте, швидко ви це зможете зробити за допомогою простого додавання і яке це буде число?Так, додавати ви будете надто довго і число буде досить великим. Тому діяти треба інакше. Якраз сьогодні ми з вами розглянемо формулу, яка надасть можливість знаходити суму n – перших членів будь-якої арифметичної прогресії. І тоді ми швидко зможемо розв`язати і ось цю задачу.

  Отже тема нашого уроку: «Сума n – перших членів арифметичної прогресії ». Нашим завданням на сьогоднішньому уроці є вивести цю формулу і навчитись її застосовувати.

V. Формування знань

Для того, щоб вивести цю формулу, ми повернемося до завдання, яке залишилося нерозв`язаним. І сформулюємо цю задачу так :

знайти суму перших ста натуральних чисел

  Цю задачу намагалися розв`яти багато математиків найлегшим і найшвидшим способом. Найкраще це вдалося видатному німецькому математику Карлу Фрідріху Гауссу. До речі , цю задачу він розв`язав будучи учнем третього класу, чим немало здивував вчителя. Як же рахував Гаусс ? (міні - презентація)

Використовуючи хід міркувань Гаусса та властивість арифметичної прогресії, виведемо загальну формулу для обчислення суми n – перших членів арифметичної прогресії ( an) : a1 ,   a2,  a3,… a n-2, an-1, an . Позначимо цю суму Sn . Запишимо цю суму двічі, розмістивши в першому випадку доданки в порядку зростання їх номерів, а у другому- у порядку спадання:

Sn  = a1 +  a2 + a3+ … +a n-2 + an-1+  an ;

Sn  = an+ an-1 + a n-2+ …+ a3+  a2 + a1 .

Тепер ці рівності додамо почленно, матимемо :

2Sn  = (a1+  an)+( a2+ an-1) +…+ ( an-1+  a2)+ (an + a1).

За властивістю арифметичної прогресії кожна сума в дужках дорівнює  (a1+  an), а доданків таких маємо n. Отже,

Поділивши обидві частини цієї рівності на 2, отримаємо формулу суми n перших членів арифметичної прогресії: , використавши формулу n- ного члена арифметичної прогресії, маємо другу формулу: , якою зручно користуватися, якщо відомо перший член і різницю прогресії.

Застосуємо формули для розв`язування вправ.

VI. Формування вмінь

Письмові вправи

 № 730 (за підручником) -  розв`язує вчитель

 № 732 – учні біля дошки

        Робота в групах (за картками)

    Форма перевірки – взаємоперевірка.

 № 742 (самостійно)

Додаткова задача

(формування компетенції підприємництва та фінансової  грамотності)

 Дмитрик протягом тижня відкладав деяку суму з кишенькових грошей, які батьки давали йому на особисті витрати. Щодня він збільшував суму для накопичення на 

 5 грн. З якої суми він починав відкладати кишенькові гроші ?

VII. Підсумки уроку

Контрольні запитання

1. За якою формулою можна обчислити суму перших ста членів арифметичної прогресії, якщо відомі:

1) а₁ і а₁₀₀;   2) а₁ і d;  3) а₁ і а₂?

2. Чи можна за формулою 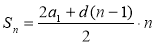обчислити суму перших десяти членів послідовності:
   1.   (а_n): 2; 3; 4; 5; 6; ...;
   2.   (а_n): 2; 4; 8; 16; 32; ...;
   3.   (а_п): n; 3n; 5n; 7n; 9n; 

      Оцінювання

VIII. Домашнє завдання

П. 17 ст. 163, вивчити формули. № 731, № 743

Підготувати історичну довідку про життя та діяльність німецького математика 

Ф.К. Гаусса