Урок на тему: "Теорема Піфагора"

Тема. Теорема Піфагора

Геометрія: підруч. для 8 кл.  загальноосвіт.  навч.  закл. / М. І. Бурда, Н. А. Тарасенкова -Київ: Оріон, 2016.

Мета:

навчальна: сформувати в учнів розуміння змісту теореми Піфагора та її доведення; формувати вміння відтворювати зміст теореми Піфагора; застосовувати її формулювання для розв'язування задач на знаходження невідомих сторін прямокутних трикутників; довести теорему різними способами;

розвивальна:розвивати логічне, критичне мислення учнів, стимулювати їх пізнавальну діяльність; розвивати вміння учнів аналізувати,  зіставаляти, робити висновки;

виховна: виховувати  прагнення до самовдосконалення; охайність побудови малюнків та культуру записів на дошці і в зошиті; прививати в учнів любов до геометрії.

Типу уроку: засвоєння нових знань.

Епіграф уроку:

Не роби ніколи того, чого ти не знаєш, але навчися всього, що слід знати, і тоді ти будеш вести спокійне життя.

(Піфагор)

Хід уроку

1. Організаційний етап

Учитель. Доброго ранку, діти! З яким настоєм ви прийшли на сьогоднішній урок?

З’ясування емоційної готовності учнів до уроку (вправа «Світлофор» За методикою Анни-Марії Богосвятської). Учні піднімають картки:

- готовий до уроку (зелений колір);

- готовий частково (оранжевий колір);

- не готовий зовсім (червоний колір).

Учитель. Я рада, що сьогодні переважає зелений, а це означає, що ви готові до праці. Сподіваюся, що на уроці, нас чекає успіх, якщо ми працюватимемо організовано і будемо компетентними в запропонованих задачах.

Епіграфом сьогоднішнього уроку буде такий вислів (слайд1), а хто є автором цих слів ви дізнаєтесь в кінці уроку.

2. Перевірка домашнього завдання

Для перевірки домашньої роботи збираються зошити.

Вчитель відповідає на запитання учнів, які виникли під час виконання завдань.

ІІІ. Актуалізація опорних знань

1.Звучить музика Чайковського “Вальс квітів”.

https://www.youtube.com/watch?v=9a4DnEWXMHM

• Як ви вважаєте, чому на уроці сьогодні звучить музика?
• Який інструмент веде головне соло в цьому музичному фрагменті? (Арфа).(слайд2)

• Чи не вважаєте ви, що є зв'язок між цим інструментом і якоюсь геометричною фігурою?  (трикутником)

2.Прийом «Запитання – відповідь» (учні по черзі задають один одному запитання про прямокутний трикутник, вчитель може допомагати учням).

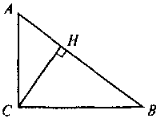
3.Виконання усної вправ за готовим малюнком (слайд 3)

1

АСВ = 90°, СН АВ. Знайдіть: 1) АС2, СН, якщо АН = 2, ВН = 8; 2) СВ, якщо АН =5, НВ = 4;

 

IV.Формулювання теми і мети уроку; мотивація навчальної діяльності(слайд 4)

1.Вчитель демонструє мотузку з вузликами.

• Як єгиптяни будували прямі кути, використовуючи мотузку?

(якщо учні не дали відповіді, тоді дають відповідь на це запитання в кінці уроку)

2.Вчитель оголошує тему:  “Теорема Піфагора”, учні записують в зошит.

Вчитель: Ви, напевно, чули про видатного давньогрецького математика Піфагор. Його ім’я носить одна з найважливіших теорем геометрії – теорема Піфагора - про співвідношення між катетами і гіпотенузою прямокутного трикутника. З неї або з її допомогою можна вивести більшість теорем. Сама ж теорема Піфагора чудова тим, що вона проста, але не очевидна. Але, крім того, теорема Піфагора має величезне практичне значення: вона застосовується в геометрії буквально на кожному кроці.

Сьогодні ми з вами на уроці доведемо цю теорему і будемо користуватись нею під час розв'язання задач.

VІ. Вивчення нового матеріалу.

1.Вчитель формулює теорему Піфагора (слайд 5)

2.Доведення 1(за підручником)

Доведення теореми Піфагора можна провести в такому порядку:

• розглянути прямокутний трикутник з катетами а і b, гіпотенузою с і висотою, проведеною до гіпотенузи hc;

• для  цього трикутника записати  метричні співвідношення для катетів;

• виконати почленне додавання обох частин здобутих рівностей;

• перетворити праву частину здобутої рівності, використавши аксіому вимірювання відрізків.(вчитель короткі записи робить на дошці)

3.Доведення 2: перегляд відео (слайд6)

https://www.youtube.com/watch?v=CAkMUdeB06o

Вчитель допомагає сформулювати класичне формулювання теореми Піфагора.(слайд6)

Вчитель: Відомо понад 300 різних доведень цієї теореми. Ще з давніх часів люди шукали і знаходили різні способи, і до цього часу знаходять все нові і нові доведення теореми Піфагора.

— Як ви думаєте: чому людина не задовольняється вже досягнутим?

— Чому її математична думка все продовжує і продовжує працювати над давно відкритим і давно обгрунтованим матеріалом? (відповіді учнів)

Вчитель:Звичайно, так було, так є і так буде завжди. Тому, що така вже природна вдача людини: вона постійно прагне до зростання, до вдосконалення, до пізнання.

Задача: знайти гіпотенузу, якщо катети дорівнюють 6 см і 8 см (с² = 6² + 8² = 100, с = 10). Таким чином демонструється практичне значення вивченої теореми.

VIІ. Закріплення нових знань і вмінь учнів

1.Виконання усних вправ

Для яких трикутників, зображених на рис. 1, виконується теорема Піфагора? Виконайте відповідні записи.(слайд 8-9)

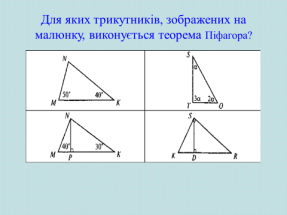
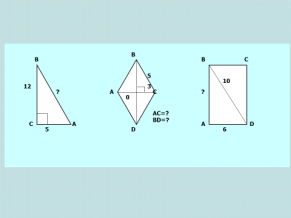
2.Виконання письмових вправ

Клас об’єднуємо у  3  групи:

І група (учні з високим рівнем навчальних досягнень з даного предмету)

ІІ група ( учні з достатнім рівнем навчальних досягнень з даного предмету)

ІІІ група (учні з початковим та середнім рівнем навчальних досягнень з даного предмету)

І і ІІ група працюють самостійно

ІІІ група колективно разом з вчителем розв’язують задачі з оформленням на дошці

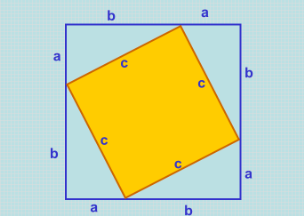Завдання для І і ІІ групи: Довести теорему Піфагора за готовим малюнком.

(Для учнів І і ІІ групи є картки- підказки, які учні можуть використати, підійшовши до вчительського стола і можна взяти тільки один листочок з підказкою. Якщо перша підказка їм недопомогла то вони беруть другу підказку і так далі…)

(Додаток1) 

 

 

 

Завдання для ІІІ групи:

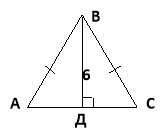1. Основа рівнобедреного трикутника 16см, а висота, проведена до основи, дорівнює 6см. Знайдіть бічну сторону трикутника.

Дано:  АС – основа, АС = 16см,

ВД – висота, ВД = 6см.

Знайти: АВ.

Розв’язання:

 ∆АВС – рівнобедрений, ВД – висота.

За властивістю висоти рівнобедреного трикутника  ВД – медіана,

АД = ДС = 8см.

∆АВД – прямокутний, за теоремою Піфагора:  

Відповідь: 10 см.

 

2. Діагональ прямокутника дорівнює 10см, а одна з його сторін 8см. Знайдіть периметр прямокутника.

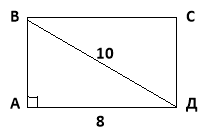                                                    Дано: АВСД – прямокутник,

ВД – діагональ,             

                                                    ВД = 10см,  АД = 8 см.

Знайти: Р.

 Розв’язання:

              Р = (АВ +ВС)× 2

 АВД – прямокутний трикутник, за теоремою Піфагора:

;  ;

Р=(6+8)× 2 = 28(см).

Відповідь: 28см.

Учні, які довели теорему Піфагора демонструють свій результат на дошці.

3.Колективне розв’язування вправи з повним оформленням на дошці

Сторона ромба дорівнює 5см, а його менша діагональ 6см. Знайдіть велику діагональ ромба.

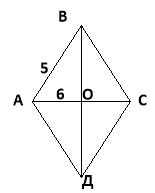                                       Розв’язання:

Ми знаємо, що за властивістю діагоналей ромба 

АСВД і АО= ОС = 3см.

Отже ∆АОВ – прямокутний.

За теоремою Піфагора: 

АВ²=АО ²+ ВО²,

(см),

ВД= 2ВО=8 (см).

Відповідь: 8см.

4.Самостійна робота

Варіант1

1.Знайдіть гіпотенузу прямокутного трикутника з катетами 6см і 8 см.

А) 10см           б) 28 см              в) см                г) 14см

2. Знайдіть катет прямокутного трикутника, якщо гіпотенуза 13см,

а катет – 5 см.

А) 8см              б) см           в)   13см              г)18см

3. Знайдіть гіпотенузу рівнобедреного прямокутного трикутника з катетом 3см.

А) 81см            б)9 см             в)   см               г) см 

4. Знайдіть сторону ромба з діагоналями 6см і 8 см.

А) 5см             б) 10см             в) 14см                 г) 196см            

 

(отримавши правильні відповіді, діти складуть необхідний пазл)

 

 

 

 

 

 

VІІІ. Підсумок уроку. Рефлексія

Вчитель:Я думаю, що ви вже догадались хто є автором епіграфу уроку (учні догадаються, що автором є Піфагор).

Якщо учні не дали відповіді на проблемне запитання, то повертаємось до нього. Якщо і вкінці уроку не можуть дати відповідь то вчитель  ставить запитання:

• Що нагадує вам мотузка? (відрізок)
• Які фігури можна скласти? (квадрат, трикутник)
• Які трикутники можна скласти? (різносторонній, рівнобедрений, прямокутний)
•  (відповіді учнів)

Вчитель:Чи пам’ятаєте ви запитання, яке вам ставила на початку уроку (Як єгиптяни будували прямі кути, використовуючи мотузку?; відповіді учнів). Стародавній спосіб побудови застосовується на будівництві і зараз.

Сьогодні на уроці ми вивчили теорему Піфагора, навчились використовувати її при розв'язанні задач. Давайте ще раз сформулюємо теорему Піфагора.

Інтерактивна вправа “Незакінчені речення”.

1.               Сьогодні на уроці ми дізналися…
2.               На сьогоднішньому уроці найважливішим відкриттям для мене було…

 «Оберіть колір вашого настрою» (За методикою Анни-Марії Богосвятської) учні визначають свій настрій, пригощаючись із запропонованих вчителем різнокольорових морських камінчиків цукеркою потрібного кольору.

Урок має свої часові межі, але бажання пізнати більше має бути безмежним. Ми дізналися лише дещицю того, що можна знайти цікавого про терему Піфагора.

Працюйте, шукайте, поглиблюйте свої знання.

ІХ. Домашнє завдання

1. Вивчити зміст та доведення теореми Піфагора § 15 (с. 110-111).

2. Дібрати цікаві факти з біографії Піфагора.

3. Розв'язати задачі №732(2), 736, 740(2).