Урок "Нескінченні періодичні десяткові дроби. "

Урок № 43                     Дата: 22.11.2018                          6Г клас

Вчитель: Чиріна А.О.

Тема уроку.  Нескінченні періодичні десяткові дроби.

Мета уроку:

• навчальна: домогтися засвоєння умови, за якої звичайний дріб можна перетворити на десятковий; сформулювати вміння записувати звичайний дріб у формі десяткового; сформувати поняття нескінченного періодичного десяткового дробу;
• розвивальна: формувати вміння аналізувати інформацію, бачити закономірності;
• виховна: виховувати старанність, наполегливість при досягненні мети.

Тип уроку: засвоєння нових знань і вмінь. Проблемний урок.

Обладнання: опорний план-конспект, смайли, комп’ютер, презентація, підручник Н.А.Тарасенкова «Математика 6», листи з завданням .

План уроку:

1. Організаційний етап (2 хв)
2. Перевірка домашнього завдання (1 хв.)
3.  Мотивація навчальної діяльності (2 хв.)
4. Формування теми і завдань уроку (2 хв.)
5. Актуалізація опорних знань (3 хв.)
6. Засвоєння знань (11 хв.)
7. Фізкультхвилинка (3 хв.)
8. Формування вмінь (15 хв.)
9. Рефлексія (1 хв.)
10. Етап інформування домашнього завдання (2 хв.)
11.  Оцінювання учнів (3 хв.)

Хід уроку

1. Організаційний етап

1. Слово вчителя

Добрий день, діти! (Cлайд 1)Сідайте. Чи всі готові до уроку?  Черговий назви відсутніх учнів. Чергові зберіть мобільні телефони.

Вітаю вас на моєму уроці. Для початку визначимо ваш настрій на початку уроку. У вас є три смайлики, які відповідають настрою. Прошу вас підняти кожен свою картку.(Слайд 2)

Більшість учнів у доброму настрої, а декілька не визначились. Я маю надію що до кінця уроку всі будуть задоволені результатом своєї роботи і матимуть гарний настрій.

2. Перевірка домашнього завдання.

Вчитель: Але перед початком уроку  давайте перевіримо домашнє завдання. Погляньте на слайд (слайді 3), тут представлені відповіді. Будь ласка швиденько порівняйте їх зі своїми. Чи все у вас так? (Одна з відповідей не співпадає з правильною) Діти знаходять помилку або вчитель їм у цьому допомагає. Виправляють.

Молодці!

Взаємоперевірка за готовими відповідями на слайді.

Вчитель: А зараз згадаємо деякі правила, які допоможуть нам на уроці. Пограємо в гру «Мікрофон»(Слайд 4)

Інтерактивна технологія «Мікрофон»

1. Сформулюйте правило множення звичайних дробів.
2. На що ділити не можна?
3. Що вийде, якщо поділити число само на себе?
4. Як ви думаєте, якщо поділити число на одиницю, то вийде….?
5. Яка дія прихована за зноком дробу?

3. Мотивація навчальної діяльності

1.       Вчитель:  Для того щоб розпочати наш урок, трошки розігріємося. (Слайд 5)

Розв’яжіть приклад представивши відповідь у десятковому дробі:

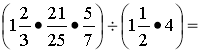
Розв’язуючи даний вираз ми натикаємось на проблему = 0,1666….

Отже поміркувавши, вирішуємо, що метою сьогоднішнього уроку – дати відповіді на такі запитання:

1. Як називається число виду 0,1666…?
2. Чи існують інші способи запису числа 0,1666…?
3. Чи можливо таке число перевести у звичайний дріб?

4. Формування теми і завдань уроку (Слайд 6)

Тема нашого уроку «Нескінченні періодичні десяткові дроби.»

Епіграф до уроку «Нехай ваш дріб завжди буде неправильним. А ідеально дорівнюв би одиниці»

Вчитель: Сьогодні на уроці ми з вами

• Дамо відповіді на поставлені запитання.
• Дізнаємося хто і коли вирішив дану проблему.
• Навчимося коректному запису і здійснимо перехід назад.

5.Актуалізація опорних знань

1. Для початку виконаємо усні вправи.(Слайд 7)

1. Виконайте ділення з отриманням десяткового дробу: 1:2; 3:20; 6:25.

2. Розкладіть на прості множники: 25; 4; 16; 15.

6. Засвоєння знань

Перейдемо до нашої основної теми(Слайд 8)

Вчені Це XVII ст. перетворенням звичайного дробу в десятковий займалися італійський математик Бонавентура Кавальєрі (1598- 1647), англійський математик Джон Валліс (1616-1703) та інші.

(1) (2)

У процесі нескінченного ділення чисельника звичайного дробу на його знаменник ці вчені отримали періодичні дроби.

(Слайд 9)У XVIII ст. періодичні дроби також вивчалися німецьким вченим Йоганом Ламбертом (1728-1777) та видатним математиком, фізиком, механіком і астрономом Леонардом Ейлером (1707- 1783)

 (1) (2)

Повну теорію періодичних дробів розробив на початку XIX ст. видатний німецький математик Карл Фрідріх Гаус (1777- 1855).

(3)

А зараз і ми з вами навчимося працювати з нескінченним періодичним десятковим дрібом. І перше, що ми з вами запишемо це що таке … (Слайд 10)

Нескінченний періодичний десятковий дріб – десятковий дріб, у якому нескінченно повторюється певна група цифр. Мінімальна група цифр, яка повторюється, називається періодом. Період записується в круглих дужках.

Наприклад: 

Якщо період починається відразу після коми, то дріб називається чисто періодичним. Якщо ж період починається не відразу після коми, то дріб називається змішаним періодичним.

7.Фізкультхвилинка

Слайд(11)

8. Формування вмінь Слайд(12)

Усні вправи розбити на три ряди, суддя найактивніша дитина

№465, 466, 469.

Робота біля дошки № 470

Робота в парах за розданим матеріалом

Відповіді (Слайд 13)

23/30-д      7/9-о        1(4/9)-б           1/3-р           3(2/9)-е

9. Рефлексія

1. Слово вчителя

А тепер підніміть смайлики, чи піднявся у вас настрій на прикінці уроку?

(Діти піднімають смайлики )

11. Етап інформування домашнього завдання (Слайд 14)

 Вчитель: Відкрийте щоденники і не забудьте записати домашню роботу:

Р. 11, № 476, 478.

12.  Оцінювання учнів

Цікаві факти (Слайд 15)

Нескоротний дріб можна записати у вигляді скінченного десяткового дробу тоді і тільки тоді, коли розклад його знаменника на прості множники не містить чисел, відмінних від 2 і 5.

У вас могло виникнути запитання, у якому випадку звичайний дріб можна подати у вигляді скінченного десяткового дробу.

Поміркуємо.

Подамо, наприклад, дроби у вигляді десяткових дробів.

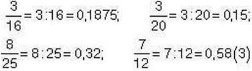
Як бачимо, перші три дроби можна подати у вигляді скінченних десяткових дробів, а четвертий – лише у вигляді нескінченного

Десяткового періодичного дробу. Розкладемо їх знаменники на прості множники:

25 = 5∙5; 16 = 2∙2∙2∙2; 20 = 2∙2∙5; 12 = 2∙2∙3.

У перших трьох розкладах містяться лише числа 2 і 5, у третьому – і число 2, і число 5. У четвертому ж розкладі є й інший множник – число 3. Це і є причиною того, що дріб не можна подати у вигляді скінченного десяткового дробу.

# 475

Перетворення нескінченного десяткового

періодичного дробу у звичайний (Слайд 16)

Чисто періодичний десятковий дріб дорівнює звичайному дробу, чисельник якого є період, а знаменник – цифра 9, що записана стільки разів, скільки цифр у періоді.

Наприклад: .

Для того щоб перетворити змішаний нескінченний періодичний дріб на звичайний, треба від числа, що стоїть до другого періоду, відняти число, що стоїть до першого періоду. Потім записати цю різницю чисельником, а в знаменнику записати цифру 9 стільки разів, скільки цифр у періоді, а після дев’яток дописати стільки нулів, скільки цифр стоїть між комою і першим періодом.

Наприклад: .

Чергові роздайте будь ласка телефони!

До побачення, ви вільні!!