Урок "Переміщення та його властивості".

Тема. Переміщення та його властивості

Мета: ознайомити учнів з прикладами геометричних перетворень і їх найпростішими властивостями; дати уявлення про переміщення фігур на площині; розвивати вміння спостерігати, узагальнювати, робити висновки; вдосконалювати навички критичного мислення, використання аналізу, синтезу, розпізнавання математичних законів у навколишньому середовищі, вміння самостійно працювати; формувати вміння і навички застосування теоретичних знань під час  розв’язування задач; виховувати поняття естетичного смаку, формувати культуру мовлення, розширювати кругозір , розвивати інтерес до предмета.

Типи уроків: засвоєння нових знань, комбіновані.

Геометрія є прообразом краси світу

Йоган Кеплер                                                      

І. Організаційний момент

Зазвичай перед першим уроком нової теми учні не мали домашнього завдання. Проте, варто ще раз додатково нагадати про труднощі, які виникли на останній контрольній роботі.

(Учитель запрошує поміркувати над епіграфом уроку, просить учнів пояснити, як вони розуміють цей рядок.)

ІІ. Мотивація навчальної діяльності

Візьміть у праву руку олівець і станьте перед дзеркалом, – і дзеркало «перетворить» вас на лівшу, адже ваш двійник триматиме олівець у лівій руці. А тепер положіть в шухляду столу лінійку; ви трохи висунули шухляду – і лінійка перемістилась разом з нею. Уявіть собі, що ви підняли колесо велосипеда і покрутили  його – колесо не зрушить з місця, але його спиці закружляють у шаленому танці. В кожному з цих випадків фігури, про які йдеться, зазнають певних змін, перетворень.

Ідея перетворень є однією з основних у сучасній математичній на­уці та в різних галузях її застосувань. За її допомогою з успіхом доводять багато тверджень, теорем з різних розділів геометрії, які виходять далеко за межі шкільного курсу. Перетворення допомагають художникам правильно будувати композиції картин, архітекторам – споруди, а хімікам – досліджувати структуру кристалів. Кінематографісти бентежать уяву глядачів дивовижними образами і незвичайними перевтіленнями на екрані за допомогою геометричних перетворень і комп’ютерної графіки.

ІІІ. Актуалізація опорних знань

Продовжте думку:

•   Якщо трикутники рівні, то відповідні сторони …
•   Якщо трикутники рівні, то відповідні кути …
•   Якщо трикутники подібні, то відповідні сторони …
•   Якщо трикутники подібні, то відповідні кути….
•   Якщо трикутники подібні, то відповідні лінійні виміри ( периметри, медіани, висоти, бісектриси, радіуси вписаних і описаних кіл) ….

Отже, у рівних трикутників відстань між двома точками зберігається, а відповідні кути рівні. У подібних трикутниках відстані між двома точками одного трикутника не дорівнюватиме відстані між відповідними точками другого трикутника, а кути – зберігатимуться.

Математики не могли обійти увагою такі цікаві властивості геометричних фігур. Їх вивчення і узагальнення привело до появи поняття геометричного перетворення.

ІV. Вивчення нового матеріалу

Історичні відомості.

Задовго до виникнення писемності – люди малювали на стінах печер, скелях, посуді різноманітні рослини, тварин тощо. Тривала практика підказувала митцям, як передати на рисунку зображуваний предмет – так зароджувалося вчення про відповідності й перетворення.

 Розробником математичних основ теорії проективних перетворень (теорії перспективи) став французький інженер і архітектор Жерар Дезарг (1593-1662). Багато талановитих учених доклали зусиль в галузі геометричних перетворень. Серед них був, зокрема, французький математик Мішель Шаль (1793-1880), який довів фундаментальну теорему про геометричні перетворення (нині відому як теорема Шаля) і французький геометр Гаспар Монж (1746-1818), який підсумував наукові пошуки в галузі геометричних перетворень створивши новий розділ геометрії - нарисну геометрію.

Пізніше на основі розподілу геометричних перетворень на групи було виділено ще декілька розділів геометрії – афінна, проективна та інші. Здобутки вчених у вивченні перетворень склали математичну основу розвитку багатьох галузей сучасної техніки.

 

           

Жерар Дезарг             Мішель Шаль            Гаспар Монж            Мауріц Корнеліс Ешер

 

В 1954 р. в Амстердамі відбулася велика виставка нідерландського художника-графіка Ешера (1898-1972), приурочена до Міжнародного математичного конгресу. Відтоді вся фізико-математична література рясніє гравюрами Ешера.

Роботи Ешера — це приголомшливі ілюстрації до математичних ідей періодичності і теорії кристалографічних груп, вони демонструють типи симетрії, застосовані в інженерній справі, геології і криптографії.

 

 

 

 

 

 

 

Якщо кожну точку однієї фігури, змістити деяким чином, то дістанемо нову фігуру. Говорять, що дана фігура утворилася перетворенням іншої.

 

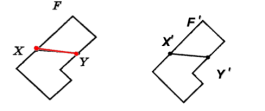
Перетворенням фігури F у фігуру F₁ називається така відповідність, при якій:

1) кожній точці фігури F відповідає єдина точка фігури F₁;

2) кожній точці фігури F₁ відповідає деяка точка фігури F;

3) різним точкам фігури F відповідають різні точки фігури F₁. 

 

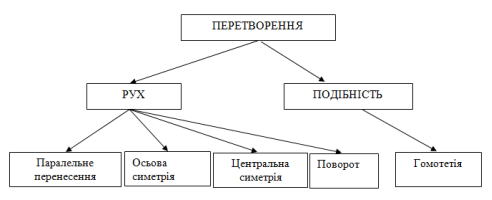
До геометричних перетворень відносять  різні види рухів (осьова та центральна симетрія, пово­рот, паралельне перенесення), подібність та гомотетія.

Перетворення однієї фігури на іншу називається переміщенням або рухом, якщо воно зберігає відстань між точками, тобто переводить  будь-які дві точки А і В першої фігури у точки А₁ і В₁ другої фігури так, що АВ = А₁В₁.  

Властивості переміщення.

1. Зберігається порядок взаємного розташування точок на прямій.
2. Прямі переходять у прямі, промені – у промені, відрізки – у відрізки.
3. Зберігаються величини кутів.
4. Два переміщення, виконані послідовно, дають знову переміщення.
5. Перетворення, обернене до переміщення, також є переміщенням.

Дві фігури називаються рівними, якщо вони переводяться переміщенням одна в одну.

 

Доведемо одну із  властивостей рухів.

Точки, які лежать на прямій, під час руху переходять у точ­ки, які лежать на прямій, і зберігається порядок їх взаєм­ного розміщення.

Доведення

Нехай точки A, B, C лежать на прямій, причому точка В — між точ­ками А і С, тобто    АВ + ВС = АС. Якщо рух відображає дані точки на точки А₁, В₁, С₁, то A₁В₁ = АВ,        A₁C₁ = АС,  B₁C₁ = ВС , тобто має місце рівність  А₁В₁ + В₁С₁ = A₁C₁. А це означає, що точка  В₁ ле­жить між точками A₁ і С₁ .

V. Засвоєння знань та формування навичок

Вправа 1 (усно)

Чи існує переміщення, яке переводить відрізок АВ на СК, якщо АВ=5см, а СК=5,1см. Відповідь обґрунтувати.

Відповідь. Ні.

Вправа 2 (усно)

При переміщені відрізок АВ переходить у відрізок СМ. Чому дорівнює співвідношення АВ:СМ?

Відповідь. 1.

Вправа 3 (усно)

При переміщенні чотирикутника АВСК дістали квадрат А₁В₁С₁К₁. Визначте довжину діагоналі АС, якщо А₁В₁=4см.

Відповідь.  4см.

Вправа 4 (усно)

При переміщенні рівнобедрений з кутом 100° переходить у . Знайти кути . Відповідь. 100°, 40°, 40°.

Вправа 5

Позначимо точки А і В. Побудуємо коло з центром в точці А радіусом 3см. Побудуйте фігуру в яку перейде коло під час руху, що переводить точку А в точку В.

Відповідь. Коло.

Вправа 6

Побудуйте відрізок АВ. Через точки А і В проведіть паралельні прямі та відкладіть від цих точок (в одному напрямі) відрізки АА₁ і ВВ₁ однакової довжини. З'єднайте точки А₁ і В₁. Порівняйте довжини відрізків: АВ і А₁В₁; АА₁ і ВВ₁. Зробіть висновок.

Відповідь. АВ = А₁В₁; АА₁ = ВВ₁.

Вправа 7

Накресліть відрізок АВ і позначте точку О, що не належить відрізку АВ. Проведіть промені АО і ВО. Відкладіть за точку О відрізки ОА₁ = ОА і  ОВ₁ = ВО. Сполучіть точки  А₁ і В₁.  Порівняйте довжини відрізків: АВ і А₁В₁. Доведіть, що АВ = А₁В₁.

Вказівка. Довести рівність трикутників.

Вправа 8

Точки М і К належать відрізку АВ (точка М лежить між точка­ми А і К). Відрізки AM, MN, NB відносяться, як 3:5:7. Під час переміщення відрізок АВ і точки М i К переходять у відрізок А₁В₁ і точки М₁ і К₁ від­повідно. Знайдіть довжину відрізка А₁К₁, якщо АВ = 45 см. Відповідь. 24см.

Вправа 9

Доведіть, що під час руху паралелограм переходить у паралелограм.

Вказівка. Розглянути сторони і діагоналі.

Вправа 10

При переміщенні прямокутника АВСМ дістали чотирикутник А₁В₁С₁М₁. В прямокутнику діагональ АС = 8см, кут між діагоналлю і стороною 30°. Знайти сторони чотирикутника А₁В₁С₁М₁.

Відповідь. 4см і 4см.

VІ. Підбиття підсумків

Запитання до класу

Що таке перетворення фігури?

Про яке геометричне перетворення ми дізнались?

Яке перетворення фігури називається переміщенням?

Чи будь-яке перетворення є переміщенням?

Як ще інакше називають переміщення?

Які основні властивості має переміщення?

Який зв'язок переміщення має з рівністю фігур?

VІІ. Домашнє завдання.

Складається з теоретичної частини – текст пункту підручника, та практичної – кількох вправ і задач, подібних до завдань класної роботи.