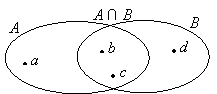
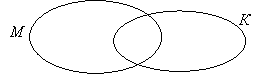
Урок «Перетин множин. Знак ∩ »

Урок 9

 

Тип урока: ОНЗ.

Тема: «Пересечение множеств. Знак ∩».

 

Цели урока:

1) Сформировать представление об операции пересечения множеств и её фиксации в речи и знаково.

2) Закрепить понятия «множество», «элемент множества», способы задания множеств.

3) Тренировать способность к составлению буквенных выражений по тексту задач.

Мыслительные операции, необходимые на этапе проектирования: анализ, синтез, обобщение, сравнение.

Демонстрационный материал:

1) опорная схема № 1:

 

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ                  А = {1, 2, 3,…9}                                                А — множество однозначных чисел   Помни: элементы множества не могут повторяться!

 

2) опорная схема № 2: 3) опорная схема № 3

 

 

 

 

 

 

 

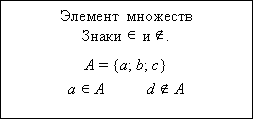
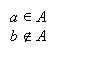
4)  карточка: 5) алгоритм расположения элементов пере-

секающихся множеств A и B на диа-

грамме Венна:

 

 

 

6) опорная схема операции пересечения:

 

 

 

 

 

 

 

 

 

 

 

Раздаточный материал:

1) два овала прозрачной разноцветной пленки у каждого учащегося;

2) карточки с числами: 1; 3; 5; 7; 9; 2; 3; 4; 5;

3) образец для самопроверки самостоятельной работы № 5 (б), стр. 26.

 

1) Построить пересечение множеств М и К.	Эталон
М = {15; 25; 30; 40} К = {23; 24; 25} М ∩ К = {25}	A = {a, b, c} B = {b, c, d} A ∩ B = {b, c}
2) Расположить элементы множеств М и К на диаграмме Венна и обвести цветным карандашом множество М ∩ К.
1. Общий элемент множеств М и К — число 25.
2. Отмечаю число 25 в области пересечения множеств М и К. Обвожу ее цветным карандашом.
3. Отмечаю числа 15, 30 и 40 вне области М ∩ К, но внутри диаграммы множества М. Отмечаю числа 23, 24 вне области М ∩ К, но внутри диаграммы множества К.

 

Ход урока:

 

1. Мотивация к учебной деятельности.

Цель:

1) мотивировать к учебной деятельности посредством актуализации позитивных ситуаций и впечатлений;

2) определить содержательные рамки урока: множества, понятие «пересечение».

Организация учебного процесса на этапе 1:

На доске запись:

A = {2; 3; 4; 5}

B = {1; 3; 5; 7; 9}

      (запись 2)

 

                                                      (рис.1)

 

 

•      Над какой темой мы сейчас работаем на уроках математики? (Над темой «Множество».)
•      Что вам в этой теме понравилось, запомнилось? (…)
•      Какая запись на доске относится к данной теме? (Вторая.)
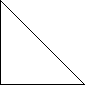
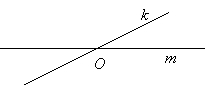
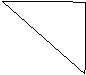
•      Что общего у этой записи с рисунками? (Обозначение латинскими буквами, есть общая точка (рис.1) , общие элементы (запись 2), общая часть (рис.3))
•      Такие прямые, так изображенные фигуры, и  такие множества в математике называют пересекающиеся.
•      Сегодня на уроке мы опишем на языке множеств понятие «пересечение», которое мы встречаем и в жизни, и в математике при изучении геометрических фигур и множеств.
•      С чего начнем урок, в котором вы узнаете что-то новое? (Сначала мы повторим материал необходимый для новой темы.)
•      И так, начнем. Пожелайте друг другу успеха.

2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.

Цель:

1) актуализировать понятие множества, способы задания множеств, графическое изображение множеств с помощью диаграммы Венна;

2) тренировать способность к установлению соответствия между действием и его результатом;

3) актуализировать представления о пересечении линий, фигур, множеств объектов и познакомить с условным обозначением действия пересечения;

4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее недостаточность имеющихся знаний для расположения элементов пересекающихся множеств на диаграмме Венна.

Организация учебного процесса на этапе 2:

1) Множества и способы их задания.

Учитель выставляет на доску опорные схемы 1–3 (см. демонстрационный материал).

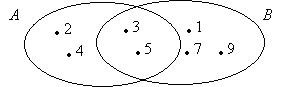
•      Как заданы множества A и B? (Перечислением элементов.)
•      Как еще можно задать множества? (Указанием общего свойства.)
•      Задайте каждое из множеств A и B общим свойством. (A — множество однозначных чисел от 2 до 5; B — множество однозначных нечетных чисел.)
•      Расставьте знаки принадлежности в следующей записи.

На доске запись:

3…A 4…A 9…A

3…B 4…B 9…B

Ученики выходят к доске по очереди и дополняют запись знаками. Остальные работают в тетрадях.

3  A 4  A 9  A

3  B 4  B 9  B

•      Где зафиксировано, что множества A и B имеют общий элемент? (В первом столбике. Число 3 принадлежит и множеству A, и множеству B.)
•      Есть ещё общий элемент в этих множествах? (Да, число 5.)
•      Запишите в тетрадях и на доске еще один столбик с элементом 5.

Запись на доске и в тетрадях:

5  A

5  B

2) Уточнение смысла понятия «пересечение». Введение знака: ∩.

•      Вернемся к записи на доске (см. этап мотивации). О каких линиях и геометрических фигурах говорят, что они пересекаются? (Линии пересекаются, если имеют общую точку; пересечением фигур является новая фигура: точка, отрезок, многоугольник…)
•      А какие множества можно назвать пересекающимися? (Когда у них есть общие
  элементы.)
•      Что вы можете сказать о множествах A и B? (Они пересекаются, так как имеют общие элементы.)
•      Какие элементы являются общими для множеств A и B? Докажите. (Числа 3 и 5: они принадлежат и множеству A, и множеству B.)
•      Мы нашли и указали общие элементы двух множеств. В математике говорят, что мы выполнили операцию пересечения множеств. Её принято обозначать знаком ∩.

Учитель вывешивает на доску карточку:

•      Запишите с помощью этого знака, что множества A и B пересекаются.

Один ученик записывает на доске, остальные в тетрадях:

A ∩ B.

•      Мы записали действие пересечения.

Учитель дописывает на доске:

A ∩ B.

 действие

•      Что нашли в результате этой операции? (Нашли общие элементы.)
•      Получили новое множество, состоящее из общих элементов этих множеств.

Учитель дополняет запись на доске:

A ∩ B   =  {3; 5}

 действие    результат

•      Сколько раз записаны общие элементы? (Один раз.)
•      Почему? (Потому что элементы множества повторяться не могут.)
•      Можем ли мы изобразить на диаграмме один и тот же элемент разными точками? (Нет.)

3) Индивидуальное задание на затруднение.

Учитель раздает детям листы формата А 4.

•      Изобразите схематически наши множества A и B и расположите их элементы на диаграмме Венна.

Дети выполняют работу самостоятельно. Учитель собирает листы учащихся и размещает их на доске, группируя по разным вариантам: отсутствие решения, неправильное расположение множеств (автономно), неправильное расположение элементов множеств, верное решение.

•      Что заметили? (Получились разные рисунки.)
•      Сможем ли мы определить, кто выполнил работу правильно? (Нет.)
•      В чём ваше затруднение?  (Нет опорной схемы для проверки.)
•      Когда мы сможем выявить верное решение? (Только тогда, когда найдем способ для проверки.)

3. Выявление места и причины затруднения.

Цель:

1) организовать выявление и фиксацию детьми места и причины затруднения;

2) организовать согласование цели и темы урока и её фиксирование.

Организация учебного процесса на этапе 3:

•      Какое задание выполняли? (Изображали диаграмму Венна множеств A и B и отмечали на диаграмме их элементы.)
•      Чем это задание отличается от тех, которые выполняли раньше? (Раньше мы строили диаграмму одного множества, а в этом задании — сразу двух множеств, которые пересекаются.)
•      Почему возникло затруднение? (Не знаем способа изображения пересекающихся множеств и расположения на диаграмме их элементов.)
•      Значит, чему вы должны научиться, поставьте перед собой цель. (Надо научиться строить диаграмму пересекающихся множеств, изображать элементы этих множеств на диаграмме.)
•      Назовите тему урока. (Пересечение множеств.)

Учитель записывает тему на доске.

4. Построение проекта выхода из затруднения.

Цель:

1) организовать взаимодействие с целью определения места пересечения множеств на диаграмме Венна; обозначению на диаграмме элементов множеств;

2) составить алгоритм расположения элементов пересекающихся множеств на диаграмме Венна;

3) зафиксировать новый способ действия в речи и знаково.

Организация учебного процесса на этапе 4:

1) У детей на партах лежат два овала прозрачной разноцветной пленки и небольшие карточки с числами — элементами множеств A и B:

1; 3; 5; 7; 9; 2; 3; 4; 5.

•      Рассмотрите предметы, которые лежат у вас на парте. Как мы можем их использовать для выполнения задания? Что они будут обозначать? (Овалы будут обозначать диаграммы множеств A и B; числа — элементы множеств.)
•      Выложите на парте овалы так, чтобы было видно, что они имеют общие элементы, пересекаются.

Дети совмещают две небольшие области овалов. Учитель фиксирует на доске, прикрепляя пленку с помощью магнитов.

 

 

 

 

 

•      Мы показали пересекающиеся множества. Какие элементы мы должны разместить в области пересечения множеств? (Общие элементы.)
•      Почему? Потому что эти элементы принадлежат и множеству A, и множеству B.
•      Сколько раз мы должны указать общие элементы? (Один раз, потому что это одни и те же числа.)
•      Сколько общих элементов множеств A и B? (2.)

Дети выкладывают в пересечение множеств общие элементы — карточки с числами 3 и 5 один раз на своих моделях, учитель прикрепляет числа скотчем.

•      Все элементы указали? (Нет, не все. Осталось указать оставшиеся элементы множеств.)
•      В какой области на диаграмме их надо обозначить? (Вне области пересечения множеств.)
•      Выложите элементы на диаграмме самостоятельно.

В результате работы получается следующая запись:

 

 

 

 

 

Учитель обращает внимание детей на задание на затруднение (см. этап актуализации).

•      Можем ли мы теперь определить, кто выполнил работу правильно? (Да.)
•      Найдите верное решение. (…)

2)  – Теперь составьте алгоритм расположения элементов пересекающихся множеств A и B на диаграмме Венна.

Дети говорят, учитель прикрепляет на доску шаги алгоритма.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. Реализация построенного проекта

Цель:

1) организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний: о выполнимости для операции пересечения множеств;

2) зафиксировать новое знание в речи, графической и знаковой форме (с помощью эталона, опорной схемы), сформировать умение использовать открытые знания на практике;

3) организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

 – А теперь постройте опорную схему операции пересечения множеств.

Работа проводится в группах.

Дети представляют свои опорные схемы и объясняют свои результаты, выводят общую опорную схему.

 

 

 

 

 

 

 

 

 

 

•      Что у вас получилось? (Опорная схема для операции пересечения множеств.)
•      Чему вы научились? (Научились выполнять операцию пересечения множеств, запи-
  сывать ее результат, обозначать элементы пересекающихся множеств на диаграмме
  Венна.)
•      Справились с затруднением? (Да.)
•      Молодцы!
•      С затруднением справились, опорную схему составили, что будете делать теперь? (Будем тренироваться)

6. Первичное закрепление с проговариванием во внешней речи.

Цель:

1.    тренировать способность к выполнению и записи операции пересечения множеств;

2) тренировать способность к расположению элементов множеств на диаграмме Венна.

Организация учебного процесса на этапе 6:

№ 5 (а), стр. 26.

Работа проводится фронтально. Учащиеся по одному выходят к доске, выполняют необходимые записи и комментируют свои действия, опираясь на опорный сигнал и шаги построенного алгоритма. Остальные учащиеся работают на печатной основе.

М = {а; б; ;}

К = {; а; в}

М ∩ К  = {а; }

 

7. Самоконтроль с самопроверкой по эталону.

Цель:

1) тренировать способность к самоконтролю и самооценке;

2) проверить своё умение применять новый алгоритм в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки..

Организация учебного процесса на этапе 7:

 № 5 (б). стр. 26.

•      Выполните задание.

Ученики самостоятельно выполняют задание в тетрадях в течение 2 минут

•      Проверьте правильность выполнения задания.

 Учитель предлагает детям готовый образец Р–3, по которому они проверяют выполненное задание.

•      Где допустили ошибку? (…). Поставьте знак «?».
•      Почему допущена ошибка? (…)
•      Исправьте свои ошибки.
•      Кто выполнил задание правильно? Поставьте справа от задания «+».

8. Включение в систему знаний и повторение

Цель:

•      тренировать способность к решению задач на пересечение множеств, составлению буквенных выражений к текстам задач.

Организация учебного процесса на этапе 7:

1) № 9, стр. 27

•      Составьте и запишите выражения к задачам.

Дети самостоятельно выполняют задание в учебниках.

•      Проверьте свою работу.

Учитель на доске пошагово открывает правильно составленные выражения, а дети проверяют работу:             

a) (а + b) : 3 г) n – а · 4

б) d : 7 · 20 д) а + а · 3 + (а · 3 – b)

в) с : (с – b)  

•      Какие ошибки допустили? (…)

Если встречается ошибка, ученик, допустивший ее, делает анализ задачи вслух и исправляет ошибку.

•      Найдите задачу на приведение к единице. (Это задача б)
•      Какова особенность решения таких задач? (В первом действии надо привести искомую величину к единице, а выбор второго действия зависит от неизвестного. Если неизвестно количество предметов, то выполняем действие деления. Если неизвестно значение величины, то выполняем действие умножения.)

2) № 7, стр. 26.

(Дополнительное задание для тех, кто раньше выполнил № 9, стр. 27.)

а) – Рассмотрите диаграмму Венна. Что вы можете сказать про множества? (Они не пересекаются.)

•      Имеют ли множества А и В одинаковые элементы? (Нет.)
•      Каким множеством будет результат пересечения непересекающихся множеств? (Пустым множеством.)
•      Запишите решение в тетрадь самостоятельно.

Ученики самостоятельно выполняют задание в тетрадях: А ∩ В = ∅

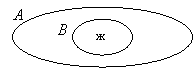
б) На доске учитель рисует диаграмму Венна и начало предложения:

 «Если А ⊂ В, то ________».

•      Рассмотрите диаграмму и сделайте вывод самостоятельно.

Дети выполняют задание самостоятельно, предлагают свои варианты записи и обсуждают фронтально. В результате они должны сделать вывод:

Если А ⊂ В, то А ∩ В = В

 

 

 

8. Рефлексия учебной деятельности на уроке.

Цель:

1) зафиксировать новое содержание, изученное в классе в виде опорных конспектов;

2) оценить собственную деятельность;

3) обсудить домашнее задание.

Организация учебного процесса на этапе 7:

•      Назовите тему сегодняшнего урока. (Пересечение множеств.)
•      Что является результатом пересечения? (Новое множество, включающее те элементы, которые принадлежат одновременно каждому из заданных множеств.)
•      Чему научились? (Научились находить пересечение множеств, строить диаграмму Венна и располагать элементы множеств на диаграммах.)
•      Достигли цель урока? (…)
•      Как вы оцениваете свою работу?

Домашнее задание:

записать в тетрадь опорных конспектов новые схемы на тему      
     «Пересечение множеств»;

 № 6 или № 10, стр. 26 — один по выбору;

☺ № 8, стр. 26, (оформить на отдельных листах).