Урок 10

Тип урока: ОНЗ.

Тема: «Свойства пересечения множеств».

 

Основные цели:

1) формировать представление о переместительном и сочетательном свойствах операции пересечения множеств;

2) повторить переместительное и сочетательное свойства сложения и умножения, закрепить понятие пресечения множеств;

3) тренировать навыки решения  уравнений и задач на приведение к единице.

Мыслительные операции, необходимые на этапе проектирования: сравнение, обобщение, аналогия.

Демонстрационный материал:

1) карточки с высказываниями:

     «Новое умение — везде найдёт применение».

     «Торопись — да не ошибись».

     «Повторение — мать учения».

2) карточки с записями:

 

 

3) карточки с записью свойств чисел (см. также эталоны из пособия «Построй свою математику» 2 класс, 3 класс):

а + b =  b + а (а + b) + с = а + (b + с)

а · b = b · а (а · b) · с = а · (b · с)

4) карточки для составления эталона:

      

 

 

 

 

 

5) алгоритм  рассуждений для вычислений:

 

 

 

 

 

 

 

 

6) эталон для самопроверки к этапу 7:

 

 

 

 

 

 

7) «лесенка успеха»

 

 

 

 

 

 

 

 

Раздаточный материал:

1. Планшеты, либо листы или экраны для выполнения заданий для пробного действия.
2. Самопроверка к заданиям по выбору (задача)

4 под. – n  кв.

6 под. — ? кв.        

1 под. — ? кв.        

Ответ: 96 квартир в 6 подъездах.

3. Самопроверка к заданиям по выбору (уравнения)

а) х – 394 = 286;               286

   х =  286 + 394; 394 

   х =  670          670

  286 + 394 = 670

  670 = 670

4. Самопроверка к заданиям по выбору (примеры)

 

а) (13 + 8 · 4 ) : 5 – (27 : 3 – 0 · 6) = 9 – 9 = 0

                 32

             45              9

 

 

 

б) 40 : (24 : 6) + 7 · (12 – 2 · 2) – 5 · 5 =  10+ 56 – 25 = 10 + 56 – 25 = 41

                  4                               4         25

        10                     56        8

 

 

Ход урока:

1. Мотивация к учебной деятельности.

Цель:

1) создать условия для возникновения у учащихся внутренней потребности включения в учебную деятельность («хочу») через создание ситуации, вызывающей интерес;

2) организовать деятельность учащихся по установке тематических рамок урока («могу»): пересечение множеств.

3) организовать актуализацию требований к ученику со стороны учебной деятельности («надо»).

Организация учебного процесса на этапе 1:

1) – Вы любите мечтать?  Воображать что-то? (…)

•      Сегодня на уроке нам пригодится ваше воображение.
•      Готовы? Тогда закройте глаза и вообразите, что мы пересекаем реку и попадаем на поле, где растёт множество цветов.

Учитель выделяет голосом слова «пересекаем» и «множество».

•      Какие математические термины вы услышали в моих словах? («Пересекаем» и «множество».)
•      Как вы думаете, что продолжим изучать сегодня на уроке? (Пересечение множеств.)
•      Сегодня вы постараетесь раскрыть ещё одну математическую тайну. А как вы раскрываете тайны? Какие два шага вы выполняете? (Остановимся, подумаем, чего мы ещё не знаем, и сами откроем  новое знание.)
•      Пожелайте друг другу удачи.
•      С чего начнём урок? (С повторения того, что нам пригодится для открытия нового.)

2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.

Цель:

1) актуализировать представление о пересечении множеств, переместительном и сочетательном свойствах сложения и умножения;

2) зафиксировать свойства сложения и умножения в виде эталона в знаковой форме и в речи;

3) организовать актуализацию мыслительных операций, достаточных для построения нового знания

4) зафиксировать ситуацию, демонстрирующую недостаточность знаний: о свойствах операции пересечения множеств.

Организация учебного процесса на этапе 2:

1) Актуализация представлений об операции пересечения множеств.

•      Посмотрите на множества.

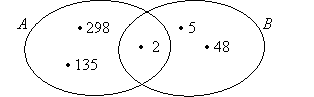На доске диаграмма пересекающихся множеств А и В.

 

 

 

 

•      Перечислите элементы множества А и множества В.
•      Что значит «общие элементы» множеств? (В множестве А есть такие же элементы, как и в множестве В.)
•      Назовите общие элементы множеств. (2.)
•      Сделайте вывод о том, какие это множества. ( Пересекающиеся, имеют общие элементы.)
•      Что называют «пересечением» множеств? (Их общую часть.)
•      Запишите множества А и В с помощью фигурных скобок.

Учащиеся записывают в тетрадях, либо на индивидуальных досках, один ученик у доски. На доске появляется запись:

А = 298; 135; 2, В = 5; 48; 2.

•      Что мы с вами сейчас сделали? (Задали множества.)
•      Когда множество считается заданным? (Если о любом предмете можно сказать, является ли он элементом этого множества.)
•      Как называется такой способ задания множества? ( Перечисление.)
•      Каким способом можно ещё задать множество? (Указанием общего свойства.)
•      Запишите общую часть множеств А и В. (А ∩ В = 2.)

Учитель расставляет между числами знаки и скобки, остальное — стирает.

На доске — математические выражения:

298 + (135 + 2)

(5  48)  2

2) Актуализация представлений о переместительном и сочетательном свойствах сложения и умножения.

•      Назовите получившиеся записи математическим термином. (Выражения.)
•      Что общего в выражениях? (По три числа, есть скобки.)
•      Чем отличаются? (Первое выражение на сложение, второе выражение на умножение.)
•      Какие свойства операций сложения и умножения вы знаете? (Переместительное, сочетательное и распределительное.)
•      Для чего используют эти свойства? (Для удобства вычислений.)
•      Найдите значения выражений, пользуясь свойствами. Каким свойством вы воспользуетесь? (Сочетательным. От изменения порядка действий сумма (произведение) не изменяется.)

Учитель вывешивает эталон:

(a + b) + c = a + (b + c)

(a · b) · c = a · (b · c)

По одному ученику комментируют с места, остальные записывают в тетрадь.

298 + (135 + 2) = 298 + (2 + 135) = (298 + 2) + 135 = 300 + 135 = 435

(5 · 48) · 2 =  (5 · 2) · 48 = 10 · 48 = 480.

На доске:

259 + 648…648 + 259

(48 ·  7) ·  5… 48 ·  (7 ·  5)

•      Сравните выражения. Каким свойством вы воспользуетесь? (Переместительным. От перестановки слагаемых (множителей), сумма (произведение) не изменяется. И сочетательным)

Учитель вывешивает на доску эталон:

a + b = b + a

      a · b = b · a  

•      Выполняются переместительное и сочетательное свойства для операций деления или вычитания? (Нет.)
•      Докажите. (Например: 7 – 3  3 – 7;  10 : 2  2 : 10;  (10 – 5) – 4  10 – (5 – 4);  и т. д.)
•      Сделайте вывод. (Не все известные нам операции обладают переместительным и сочетательным свойствами.)
•      Что мы с вами сейчас повторили? (Множества, пересечение множеств, переместительное и сочетательные свойства умножения и сложения, сравнивали выражения).
•      Какой следующий шаг в нашей работе? (Вы нам дадите задание на пробное действие)
•      Зачем? (чтобы мы поняли, чего мы ещё не знаем)

3) Задание для пробного действия.

•      Вы сейчас прекрасно справились со сравнением. Определите, верны или неверны следующие равенства.

А ∩ В = В ∩ А

(А ∩ В) ∩ С = А ∩ (В ∩С)

- Что нового в этом задании? (Надо определить, верны равенства с пересечениями или нет, а мы такого никогда не делали).

- Попробуйте выполнить задание.

Дети выполняют задание либо на индивидуальных досках, либо на отдельных листах.

- Проверим выполнение. Кто не справился с заданием? В чём ваше затруднение? (Мы не можем определить, равны эти пересечения или нет.)

- Кто определил, верны или нет эти равенства?

Фиксируются все ответы детей.

- Докажите, что вы правы. На какой эталон вы опирались? (У нас нет данного эталона.)

- В чём ваше затруднение? (Мы не можем обосновать свой ответ.)

 

3. Выявление места и причины затруднения.

Цель:

1) организовать восстановление выполненных операций и фиксацию (вербальную и знаковую) места – шага, операции, где возникло затруднение;

2) организовать соотнесение действий учащихся с используемым способом (алгоритмом, понятием и т.д.) и на этой основе организовать выявление и фиксирование во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостаёт для решения исходной задачи такого класса или типа.

 

Организация учебного процесса на этапе 3:

•      Какое задание вы выполняли? (Мы должны были определить, верно ли то, что пересечения множеств равны.)
•      Как вы выполняли задания? (…)
•      Где у вас возникло затруднение?
•      Почему оно возникло? (У нас нет правила, эталона, чтобы определить, верны ли эти равенства.)
•      Что помогло нам сравнить числовые выражения? (Свойства сложения и умножения.)
•      Посмотрите на эталоны, которые висят на доске. На какие из них похожи данные равенства? (Первая – на переместительное свойство умножения и сложения, вторая – на сочетательное…)
•      А, может быть, данными свойствами обладают и пересечения множеств? И именно эти знания помогут нам.

4. Построение проекта выхода из затруднения.

Цель:

в коммуникативной форме организовать построение учащимися проекта будущих учебных действий:

1. уточнение цели проекта (определить, действуют ли переместительное и сочетательное свойства на пересечение множеств);

2. определение средств (алгоритмы, модели, учебник и т.д.);

3. составить план действий.

•      Значит, какую цель поставим перед собой? (Выяснить, обладает ли пересечение множеств переместительным и сочетательным свойствами, записать и  сформулировать его.)
•      Сформулируйте тему урока. («Свойства пересечения множеств».)

Учитель вывешивает табличку с названием темы на доску.

- Вспомните ещё раз, что мы повторяли. Подумайте, что поможет вам доказать, что пересечения множеств обладают свойствами сочетательным и переместительным, а значит, и что эти равенства верны.(…)

- Умеем мы задавать множества? Умеем обозначать их на диаграммах?

План:

1. задать множества А, В и С перечислением, таким образом, чтобы они имели общие элементы, пересечение;
2. зафиксировать данные пересечения в диаграммах Венна;
3. сделать вывод;

5. Реализация построенного проекта.

Цель:

1) организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний: о выполнимости для операции пересечения множеств  переместительного и сочетательного свойств;

2) зафиксировать новое знание в речи, графической и знаковой форме (с помощью эталона, опорной схемы), сформировать умение использовать открытые знания на практике;

3) организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

•      Проверим, обладает операция пересечения множеств  переместительным и сочетательным свойствами или нет.

Форма работы: групповая на планшетах или листах.  Педагог предварительно повторяет с детьми правила работы в группах.

Другой вариант работы. Если дети по каким-либо причинам не готовы к групповой работе и самостоятельным выводам, то возможна работа под руководством учителя.

•      Зададим множества А, В и С перечислением. (Дети предлагают свои варианты множеств, учитель фиксирует любой вариант на доске.)
•      Изобразим с помощью диаграммы Венна множество А, множество В. Что заметили? (Они имеют общие элементы, их пересечение равно…)
•      Изобразим множество В, множество А. Что заметили? (Получился такой же результат.)
•      Какой вывод вы можете сделать? (Пересечение множеств обладает переместительным свойством.)

Аналогично проводится работа над сочетательным свойством пересечения множеств.

Группы представляют результат своей работы. Приходят к выводу, что равенства  верны. Что пересечения множеств обладают переместительным и сочетательным свойствами.

- Где можем проверить наш вывод? (В учебнике.)

Обращаются к учебнику стр. 28, проверяют себя.

Учитель на доску вывешивает эталон:

 

 

 

 

 

•      Что мы доказали? (Что пересечение множеств обладает переместительным и сочетательным свойствами, а стало быть, предложенные нам равенства верны.)
•      Справились с затруднением? (Да.)
•      Молодцы!
•      Только ли пересечения конкретных множеств (тех, что мы задали) обладают данными свойствами? (Пересечения любых множеств обладают данными свойствами, ведь разные группы задавали разные множества, и для всех равенства оказались верными.)

6. Первичное закрепление с проговариванием во внешней речи

Цель:  

•      зафиксировать изученные свойства множеств во внешней речи.

Организация учебного процесса на этапе 6:

1) На доске появляется карточка с выражением:

«НОВОЕ УМЕНИЕ ВЕЗДЕ НАЙДЁТ ПРИМЕНЕНИЕ».

•      Прочитайте предложение.
•      Как вы думаете, чем займёмся? (Будем применять новое умение в заданиях.)
•      Начнём с № 2 стр. 28. Прочитайте задание.

 

 

 

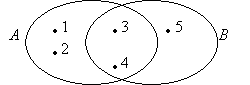
•      Перечислите элементы множества А. (А = {1; 2; 3; 4}.)
•      Перечислите элементы множества В. (В = {3; 4; 5}.)
•      Какие элементы являются общей частью множеств А и В, В и А? (Элементы 3 и 4.)
•      Запишите элементы множеств А и В и отметьте их на диаграмме. (А ∩ В = {3; 4},
  В ∩ А = {3;4}.)
•      Докажите. (Пересечение множеств не зависит от порядка множеств.)

 

 

 

 

 

 

2) № 3, стр. 28

•      Прочитайте задание.
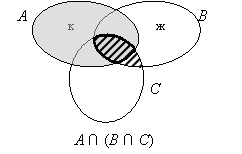•      Чем отличаются записи (А ∩ В) ∩ С = А ∩ (В ∩ С)? (В первом случае сначала находится пересечение множеств А и В, затем  его пересечение с множеством С. Во втором случае, наоборот, сначала находится В ∩ С, а затем его пересечение с А.)

                  

 

 

 

 

 

 

 

 

•      Сделайте вывод. (Пересечение множеств не зависит от порядка действий.)

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися заданий на новые понятия;

2) организовать самооценку детьми правильность выполнения задания (при необходимости – коррекцию возможных ошибок).

 

На доске карточка с выражением: « ТОРОПИСЬ — ДА НЕ ОШИБИСЬ!»

•      Прочитайте предложение.
•      Как вы думаете, к какому виду деятельности подходит это выражение? (Самостоятельной работе.)
•      С какой целью мы выполняем самостоятельную работу? (Чтобы выяснить, как усвоили новые знания.)
•      Выполните № 4 стр. 28 самостоятельно.

Так как на данном уроке подтверждалось правило и проверяется усвоение нового правила, то перед выполнением работы учитель закрывает эталон на доске, а после ее выполнения — открывает эталон для самопроверки:

 

 

 

Проверка:

•      Поставьте знак «+», если вы выполнили так же, «?» если по-другому.
•      Какие были затруднения? (…)
•      Исправьте ошибки.

8. Включение в систему знаний и повторение.

Цель: 

1) тренировать вычислительные навыки через решение примеров с использованием свойств для сложения и умножения;

2) повторить решение задач на приведение к единице, составление и решение уравнений, порядок действий в выражениях со скобками;

3) проверить у детей способность к оценке собственных достижений.

Организация учебного процесса на этапе 8:

- Новые знания помогут нам в дальнейшем при решении задач, но мы с ними встретимся на других уроках.

На доске карточка с выражением: «ПОВТОРЕНИЕ — МАТЬ УЧЕНИЯ».

•      Прочитайте выражение и  подумайте, чем мы продолжим заниматься? (Повторим те знания, которые изучили раньше.)

1) № 6 стр. 29.

Ученик с места читает задание.  

 

На доску учитель вывешивает алгоритм рассуждений для вычислений.

 

 

 

 

 

 

•      Следуя шагам алгоритма, выполните действия.

Образец рассуждения:

•      Читаю выражение: (298 + 386) + 102.
•      Определяю свойство: переместительное и сочетательное свойства сложения.
•      Вычисляю: (298 + 386) + 102 = (386 + 298) + 102 = 386 + (298 + 102) = 386 + 400 = 786.

Аналогично выполняются другие выражения.

•      Какая ещё операция обладает переместительным и сочетательным свойствами? (Операции умножения, пересечения множеств.)

Форма работы: индивидуальная.

Решение задания по выбору.

Если класс работает в быстром темпе, дальнейшую работу предлагается провести вариативно. Учащиеся, по желанию выбирают одно из заданий № 7, 9, 11 стр. 29.

Перед выбором учитель даёт установку к заданиям.

•      Если вы выберите № 7 стр. 29, то проверите своё умение решать задачи.
•      Если у вас трудности в решении уравнений, полезно будет выполнить № 9 стр. 29.
•      Выполнение № 11 стр. 29 повысит ваши вычислительные навыки.
•      Но вы можете выбрать и то задание, которое вам больше понравилось.

На доске учитель фиксирует:

№ 7 (а) стр. 29 – задача;

№ 9 (а, б) стр. 29 – уравнение;

№ 11 стр. 29 – вычисления.

После выполнения заданий, выставляются образцы их решений Р–2, Р–3 и Р–4.

Самопроверка по образцам.

Р–2

4 под. – n  кв.

6 под. — ? кв.        

1 под. — ? кв.        

Ответ: 96 квартир в 6 подъездах.

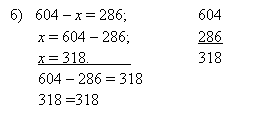
Р–3

а) х – 394 = 286; 286

х =  286 + 394; 394 

х =  670          670

286 + 394 = 670

670 = 670

Р–4

 

а) (13 + 8 · 4 ) : 5 – (27 : 3 – 0 · 6) = 9 – 9 = 0

                 32

             45              9

 

 

 

б) 40 : (24 : 6) + 7 · (12 – 2 · 2) – 5 · 5 =  10+ 56 – 25 = 10 + 56 – 25 = 41

                  4                               4         25

        10                     56        8

 

9. Рефлексия учебной деятельности на уроке.

Цель:  

1) зафиксировать новое содержание, изученное на уроке;

2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;

3) оценить собственную деятельность;

4)зафиксировать неразрешенные на уроке затруднения, если они есть, как направления будущей учебной деятельности;

5) обсудить домашнее задание.

Организация учебного процесса на этапе  9:

•      Что нового узнали на уроке? (Операция пересечения множеств обладает переместительным и сочетательным свойствами.)
•      У кого остались вопросы на конец урока?
•      Кто хорошо разобрался в теме? Молодцы!
•      Где нам пригодится новое знание? (При работе с множествами.)
•      Кто может доказать, что он находился в учебной деятельности?
•      Какие задания ещё выполняли? Что понравилось больше?
•      Над чем ещё следует поработать?
•      Возьмите экраны и на «лесенке успеха» отметьте ту ступеньку, на которой вы оказались к концу урока.

Первая ступенька — многое не понял и остались вопросы; вторая ступенька — во время работы было много трудностей; третья ступенька — многое понял, но были ошибки; четвертая ступенька — трудности преодолены.

 

Домашнее задание:

  № 5 стр. 29, № 8 стр. 29;

☺ № 10 стр. 29, № 13 стр. 30;

 № 14* стр. 30.