Урок "Перетворення неправильного дробу в мішане або натуральне число та мішаного числа у неправильний дріб"
Конспект уроку з математики для 5-го класу
Тема: Перетворення неправильного дробу в мішане або натуральне число та мішаного числа у неправильний дріб. Самостійна робота.
Мета: формувати поняття, «ціла і дробова частина числа», алгоритми виділення цілої частини з неправильного дробу, перетворення неправильного дробу в натуральне число, перетворення мішаного числа у неправильний дріб;
розвивати творчі здібності, кмітливість учнів, уміння грамотно висловлювати свої думки;
виховувати позитивне ставлення до знань, наполегливість.
Тип уроку: засвоєння нових знань, умінь та навичок.
Наочність та обладнання: опорний конспект, підручник «Математика 5 клас, Тарасенкова», цукерки, мультимедійний проектор, презентація до даного уроку, роздатковий матеріал (індивідуальні завдання, пам’ятка для учня, самостійна робота).
Хід уроку
І. Організаційний етап. (1 хв)
Всі почули вже дзвінок.
Він покликав на урок,
Кожен з нас приготувався,
На перерві постарався.
Зараз сядуть лиш дівчатка,
А за ними – і хлоп ятка.
ІІ. Перевірка домашнього завдання. (2 хв)
Найперше ми з вами зараз перевіримо правильність виконання вами домашнього завдання (звіряємо з екраном).
№ 926
Запишіть 1 у вигляді дробу з чисельником:
-
1=
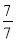 ; 4) 1=
; 4) 1=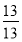 ;
;
-
1=
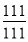 ; 5) 1=
; 5) 1= 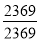 ;
;
-
1=
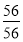 ; 6) 1=
; 6) 1=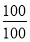 .
.
№ 928
Запишіть число 5 у вигляді дробу з чисельником:
-
5=
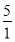 ; 4) 5=
; 4) 5=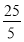 ;
;
-
5=
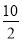 ; 5) 5=
; 5) 5= 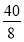 ;
;
-
5=
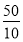 ; 6) 5=
; 6) 5=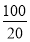 .
.
№932
Порівняйте:
-
8:3 <
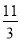 ; 3) 125:15 >
; 3) 125:15 > 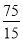 ;
;
-
25:12 <
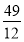 ; 4) 124:17 >
; 4) 124:17 > 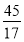 .
.
ІІІ. Актуалізація опорних знань. (4 хв)
Дивіться, мені сніговичок передав для вас ось таку сніжку. Зараз ми будемо кидати її один одному, відповідаючи на запитання по темі дроби.
- для чого було введено поняття звичайного дробу? (для лічби частин)
- що означає риска дробу? (дію ділення)
- що таке чисельник дробу і на що він вказує? (число, що стоїть над дробовою рискою, показує кількість взятих частин цілого)
- що таке знаменник дробу і що він показує? (число, що стоїть під рискою дробу, показує на скільки частин поділено ціле)
- який дріб називають правильним? (в якого чисельник менший за знаменник)
- який дріб називають неправильним? (в якого чисельник більший за знаменник)
- що мішане число? (це сума цілої та дробової частин)
- яким дробом є дробова частина мішаного числа? (правильним)
Молодці!
IV. Мотивація навчальної діяльності, повідомлення теми та мети уроку. (2 хв)
Діти, так як це перший ваш відкритий урок математики у старших класах, то щоб вас трішки заспокоїти і підняти вам настрій, я підготувала для вас невеличкий сюрприз – мішечок з цукерками і хочу вас пригостити. Ой, але у мене 42 цукерки, а вас 28, що ж робити? Як же поділити ці усі цукерки між вами так, щоб ніхто не образився? Так, правильно. Нам потрібно 42 цукерки поділити на 28 учнів. У нас вийде з вами неправильний дріб ![]() , але що ж він означає? По скільки цукерок я вам повинна роздати? Відповіді на ці запитання ми отримаємо в процесі уроку. Адже, як говорив Цицерон: «Без знання дробів ніхто не може визнавати, що знає математику». Ось ми і наблизились до нашої сьогоднішньої теми. Відкриваємо свої робочі зошити, записуємо число, класна робота, і тему уроку, яку ви бачите на екрані.
, але що ж він означає? По скільки цукерок я вам повинна роздати? Відповіді на ці запитання ми отримаємо в процесі уроку. Адже, як говорив Цицерон: «Без знання дробів ніхто не може визнавати, що знає математику». Ось ми і наблизились до нашої сьогоднішньої теми. Відкриваємо свої робочі зошити, записуємо число, класна робота, і тему уроку, яку ви бачите на екрані.
V. Засвоєння нових знань, умінь та навичок. (5 хв)
План вивчення нового матеріалу
- Виділення цілої частини з неправильного дробу.
Щоб виділити цілу частину з неправильного дробу або неправильний дріб перетворити у мішане число, чисельник якого не ділиться без остачі на знаменник, достатьно поділити чисельник на знаменник. Частка буде цілою частиною, а остача буде чисельником дробової частини із таким самим знаменником, як у неправильного дроба.
Наприклад:
![]()
- Перетворення неправильного дробу у натуральне число.
Якщо чисельник неправильного дробу ділиться націло на його знаменник, то неправильний дріб перетвориться у натуральне число.
Наприклад:
![]()
- Перетворення мішаного числа у неправильний дріб.
Щоб перетворити у неправильний дріб мішане число, достатньо помножити цілу частину на знаменник дробової частини і до отриманого добутка додати чисельник, знаходячи таким чином чисельник неправильного дробу із тим самим знаменником, що й у дробової частини мішаного числа.
Наприклад:
![]()
А чи знали ви, що існує німецьке прислів’я : «потрапити в дроби», що означає опинитися у скрутному становищі. А причина полягала в тому, що не було встановлено загальних правил виконання дій з дробами, не було створено відповідної теорії. На сьогоднішній день ми вже знаємо правила. Я сподіваюся, що ви на уроці не «потрапите у дроби».
 Пам’ятка для учня (додаток 1)
Пам’ятка для учня (додаток 1)
VІ. Фізкультхвилинка. (2 хв)
«Якщо ти щасливий, роби так…
If you happy and you know it…»
VІI. Застосування набутих знань, умінь та навичок. (15 хв)
- Усно: № 924.
№924
|
Частка |
Дріб |
Ділене |
Дільник |
Чисельник |
Знаменник |
|
3:5 |
|
3 |
5 |
3 |
5 |
|
13:7 |
|
13 |
7 |
13 |
7 |
|
5:15 |
|
5 |
15 |
5 |
15 |
|
5:17 |
|
5 |
17 |
5 |
17 |
2. Письмово: № 933; 937; 943; 949; 951; 955.
№933
Виділіть цілу частину з неправильного дробу
-
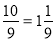 ; 4)
; 4) 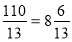 ;
;
-
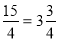 ; 5)
; 5) 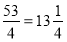 ;
;
-
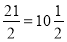 ; 6)
; 6) 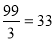 .
.
№935
Запишіть неправильний дріб у вигляді мішаного числа
-
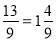 ; 4)
; 4) 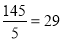 ;
;
-
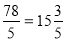 ; 5)
; 5) 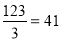 ;
;
-
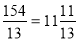 ; 6)
; 6) 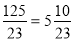 .
.
№937
Запишіть у вигляді частки мішане число
1) ![]() ; 3)
; 3) ![]() ;
;
2) ![]() ; 4)
; 4) ![]() .
.
№939
Запишіть мішане число у вигляді неправильного дробу
1) ![]() ; 3)
; 3) ![]() ;
;
2) ![]() ; 4)
; 4) ![]() .
.
№941
Шматок джинсової тканини розрізали на 12 рівних частин, три з них пішли на пошиття брюк, а інші — на пошиття курток. Яку частину тканини витратили на пошиття брюк, а яку — на пошиття курток?
Розв’язання:
1) ![]() — тканини витратили на пошиття брюк;
— тканини витратили на пошиття брюк;
2) ![]() (ч.) — витратили на пошиття курток;
(ч.) — витратили на пошиття курток;
3) ![]() — тканини витратили на пошиття курток.
— тканини витратили на пошиття курток.
Відповідь: ![]() ;
; ![]() .
.
№943
Виділіть цілу частину з неправильних дробів: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Запишіть отримані числа в порядку зростання. Який із цих дробів найбільший?
. Запишіть отримані числа в порядку зростання. Який із цих дробів найбільший?
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
В порядку зростання: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Найбільший дріб:
. Найбільший дріб: ![]() .
.
3.Додатково: № 947, 949.
VІІI. Самостійна робота. (10 хв)
 ІX. Домашнє завдання. (1 хв)
ІX. Домашнє завдання. (1 хв)
Вивчити §24
Розв’язати № 936; 940; 948.
Додатково № 956.
X. Підсумки уроку. (3 хв)
Отже, по скільки цукерок ви повинні отримати? Вірно, ![]() . Тобто по 1 і ще по пів, а якщо говорити мовою дробів, то по
. Тобто по 1 і ще по пів, а якщо говорити мовою дробів, то по ![]() цукерки. Я роздаю вам солодощі, а ви в цей момент робите самоаналіз за схемою яку ви бачите на екрані. Отож, …
цукерки. Я роздаю вам солодощі, а ви в цей момент робите самоаналіз за схемою яку ви бачите на екрані. Отож, …
Діти і на завершення хочу вас запитати. Як ви думаєте, що важливіше: що ви про себе думаєте чи що про вас думають інші?
Один з відомих письменників (Лев Толстой) сказав, що людину можна оцінювати дробом, чисельник якого становить те хороше, що вона думає про себе сама, а знаменник – те хороше, що про цю людину думають інші. То ж бажаю вам, щоб дріб у кожного із вас був завжди правильним.
Дякую усім за урок.


про публікацію авторської розробки
Додати розробку
