Урок "Піраміда. Окремі види пірамід. Піраміда, у якої усі бічні ребра рівні."

Тема уроку: Піраміда. Окремі види пірамід. Піраміда, у якої усі бічні ребра рівні.

Мета уроку: - розглянути властивості піраміди, у якої усі бічні ребра рівні; - продовжити формувати навички робити зображення піраміди, залежно від її виду; розв’язувати задачі на обчислення елементів піраміди;

- розвивати просторові уявлення, логічне мислення та культуру мовлення.

План уроку

1.     Організаційний момент.

2.     Перевірка домашнього завдання.

3.     Актуалізація опорних знань.

4.     Мотивація навчальної діяльності.

5.     Вивчення нового матеріалу.

6.     Закріплення нового матеріалу.

7.     Домашнє завдання.

8.     Підсумок уроку.

Хід уроку

1.     Організаційний момент

2.     Перевірка домашнього завдання

Відповіді на питання, що виникли при виконанні домашнього завдання.

3.     Актуалізація опорних знань

УСНО

1.     Дано п’ятикутну піраміду  MABCDF (рис.1). Назвіть  вершину, основу, ребра, бічні ребра, сторони основи, бічні грані піраміди.

2.     У п’ятикутної піраміди (рис.1):

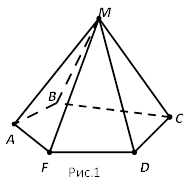кількість вершин дорівнює …, кількість бічних ребер дорівнює …, кількість ребер дорівнює …, кількість граней дорівнює …,

кількість бічних граней дорівнює …,

кількість усіх двогранних кутів дорівнює …, кількість двогранних кутів при основі … ПИСЬМОВО

3. 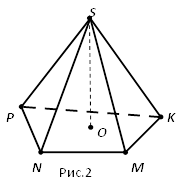    SKMNP - чотирикутна піраміда, МО – її висота

(рис. 2). 

1). Побудуйте кут нахилу бічного ребра SK до площини основи піраміди. Обґрунтуйте.         2) Побудуй лінійний кут двогранного кута при ребрі МК.

4.     Пригадайте з 10 класу властивість точки, рівновіддаленої від вершин многокутника.

(Якщо   точка          рівновіддалена     від     вершин многокутника, то вона проєктується в центр описаного навколо многокутника кола).

5.     Повторіть положення центра і формули радіусів описаних кіл навколо многокутників.

5 Вивчення нового матеріалу.

Опорна задача.

Якщо бічні ребра піраміди рівні, або нахилені до площини основи під рівними кутами, то вершина піраміди проєктується в центр описаного навколо основи кола.

Доведемо це. 

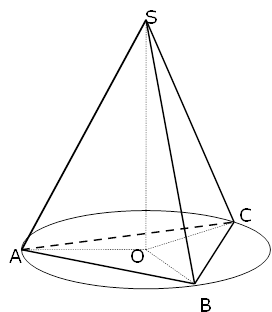Розглянемо трикутну піраміду SABC, у якої усі бічні ребра рівні. Проведемо висоту       піраміди.    SO(АВС). Тоді ΔSAO=ΔSBO=ΔSCO       (як     прямокутні трикутники з рівними гіпотенузами та спільним катетом). Отже, АО=ВО=СО. Тобто точка О - центр описаного навколо основи піраміди кола. 

Аналогічно       з        рівності      трикутників випливає рівність кутів нахилу бічних ребер піраміди до площини основи.

6. Закріплення нового матеріалу.

Задача 1. 

На рисунках  3– 5  зображені піраміди, у яких основою висоти є центр кола, описаного навколо основи піраміди. Встанови вид трикутника, що лежить в основі піраміди. 

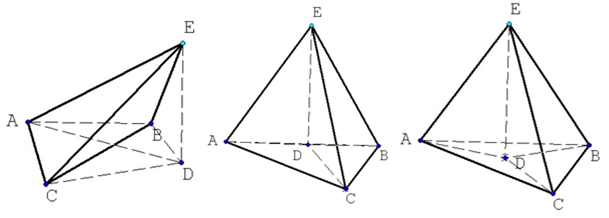
                      Рис. 3                                                                Рис. 4                                                        Рис. 5

Задача 2. (за підручником О. Істер «Геометрія» 11 клас) № 3.53

Основою піраміди є трикутник зі сторонами 13см, 14 см, 15 см. Усі бічні ребра піраміди нахилені до площини основи під однаковим кутом. Знайдіть бічні ребра піраміди, якщо її висота дорівнює 19,5 см.

Розв’язання

Так як усі бічні ребра піраміди нахилені до площини основи під однаковим кутом, то основа висоти піраміди є центром описаного навколо основи піраміди кола.

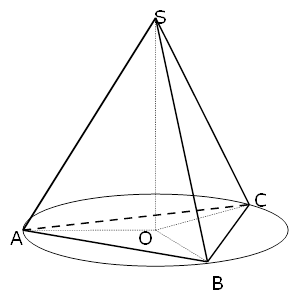
Нехай дано піраміду SABC. У ΔАВС

                                                                                                      АВ=13см,    АС=14     см,    ВС=15      см. 

SO(АВС), де О - центр описаного кола навколо ΔАВС. Тоді АО=ВО=СО радіуси описаного кола. Шукані бічні ребра AS=BS=CS. 

Знайдемо АО за формулою  𝑅 ^𝑎𝑏𝑐, де 𝑆 = √𝑝(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐).

Обчислимо 𝑝 (см).

Отже, 𝑆 = √21(21 − 13)(21 − 14)(21 − 15) = 84  (см²). 

Відповідно АО

Розглянемо ΔАОS (∠О=90⁰), за теоремою Піфагора AS²=AO²+SO². Маємо, що АS=21, 125 (см).

Відповідь: 21,125 см.

Задача 3. (за підручником А.Г. Мерзляк «Математика» 11 клас). № 18.26

Основою піраміди є прямокутник зі сторонами 6 см і 8 см, а кожне бічне ребро утворює з площиною основи кут 60⁰. Знайдіть висоту піраміди.

Розв'язання

Так як усі бічні ребра піраміди нахилені до площини основи під однаковим кутом, то основа висоти піраміди є центром описаного навколо основи піраміди кола.

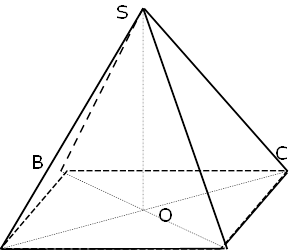
Нехай дано піраміду SABCD, де ABCD прямокутник і АВ=6 см, AD=8 см. SO⊥(АВС), де О - центр описаного кола навколо прямокутника і є точкою перетину      його       діагоналей. Тоді

A                                  D        АО=ВО=СО=DO радіуси описаного 

кола, які дорівнюють половині діагоналі прямокутника. ∠𝑆𝐵𝑂 = 60⁰ кут нахилу бічного ребра до площини основи піраміди. SO шукана висота піраміди.

Знайдемо довжину діагоналі прямокутника з ΔАВD (∠A=90⁰), за теоремою Піфагора BD²=AB²+AD². Маємо BD=10 см. Тоді ВО=5 см. Розглянемо ΔВОS (∠О=90⁰), в ньому 𝑡𝑔∠𝑆𝐵𝑂 = ^𝑆𝑂. Отже, SO= ВОtg60⁰.

𝐵𝑂

SO см.

Відповідь: .

7.     Домашнє завдання.

Вивчити теорію за конспектом. Розв’язати задачі.

Задача 1. Основою піраміди є трикутник зі сторонами 5 см, 5 см і 8 см. Усі бічні ребра нахилені до площини основи під кутом 60⁰. Знайдіть довжину висоти піраміди.

Задача 2. Основою піраміди є прямокутний трикутник, гіпотенуза якого дорівнює 32 см. Висота піраміди дорівнює 12 см. Знайдіть бічні ребра піраміди, якщо вони рівні.

8.     Підсумок уроку.