Тема уроку.   Піраміда, види пірамід, властивості

Мета уроку: формування понять піраміда, основа, вершина, бічні ребра, висота  

                       піраміди, вмінь учнів знаходити елементи піраміди.

                       розвивати просторову уяву, пам'ять, уміння проводити аналогії; 

                      виховувати наполегливість, працьовитість.

Обладнання: моделі пірамід.

Тип уроку: комбінований

                                                   Хід уроку

І. Організаційний етап

ІІ. Перевірка знань учнів

1. Фронтальне опитування.

1) Дайте означення паралелепіпеда.

2) Сформулюйте відомі вам властивості граней і ребер паралелепіпеда.

3) Сформулюйте відомі вам властивості діагоналей паралелепіпеда.

4) Чим є для паралелепіпеда точка перетину його діагоналей?

Математичний диктант

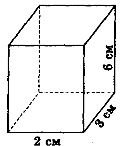
Виміри прямокутного паралелепіпеда дорівнюють:

варіант 1—3 см, 2 см і 6 см (рис. 60);

Знайдіть:

а) довжину діагоналі паралелепіпеда;

б) довжину діагоналі найменшої грані;

в) площу найбільшої грані;

г) площу найменшої грані;

д) суму відстаней від точки перетину діагоналей паралелепіпеда до всіх його вершин.

Відповідь. Варіант 1. а) 7 см; б) см; в) 18 см²; г) 6 см²;

д)28 см.

Самостійна робота

В основі прямого паралелепіпеда лежить ромб. Висота паралелепіпеда дорівнює

8 см, діагоналі паралелепіпеда дорівнюють:

варіант 1 — 10 см і см;

варіант 2 — 17 см і 10 см. Знайдіть:

а) довжину більшої діагоналі основи;

б) меншу діагональ основи;

в) сторону основи паралелепіпеда;

г) площу основи паралелепіпеда;

Відповідь.

Варіант 1. а) 6 см; б) 5 см; в) см; г) 15 см²;

Варіант 2. а) 15 см; б) 6 см; в) см; г) 45 см²;

III. Сприйняття та усвідомлення нового матеріалу

Піраміда   

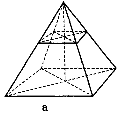
n-кутною пірамідою називається многогранник, одна грань якого — довільний n-кутник, всі інші n граней — трикутники, що мають спільну вершину.

Демонструються моделі пірамід.

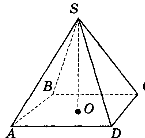
Спільну вершину трикутних граней називають вершиною піраміди, протилежну їй грань — основою, а всі інші грані — бічними гранями піраміди.

Відрізки, що сполучають вершину піраміди з вершинами основи, називають бічними ребрами.

Перпендикуляр, опущений з вершини піраміди на площину її основи, називають висотою піраміди. Висотою також називають і довжину цього перпендикуляра.

На рис. зображено чотирикутну піраміду SABCD; точка S — її вершина, ABCD — основа; SA, SB, SC, SD — бічні ребра; АВ, ВС, CD, AD — ребра основи, SO — висота. Трикутну піраміду називають також тетраедром.

Розв'язування задач

1.          Скільки граней, ребер має n-кутна піраміда?

(Відповідь, n+1 граней, 2п ребер.)

2. Чи можуть бічні ребра піраміди бути рівними, якщо в її основі лежить:

а) прямокутник; б) ромб (відмінний від квадрата);

в) правильний шестикутник; г) трапеція?

3. Чи можуть бічні грані піраміди бути однаково нахилені до основи піраміди, якщо в основі піраміди лежить:

а) прямокутник (відмінний від квадрата); б)ромб; в) трапеція?

Правила зображення піраміди

Зображення піраміди можна починати із зображення її основи. Правила зображення многокутників нам відомі. Згадаємо їх.

Запитання до класу

1) Як зображуються рівносторонній, рівнобедрений, прямокутний трикутники?

2) Що є зображенням паралелограма (прямокутника, ромба, квадрата)?

3) Що є зображенням трапеції (рівнобічної, прямокутної)?

4) Що є зображенням довільного чотирикутника (не паралелограма і не трапеції)?

5) Що є зображенням правильного шестикутника?

Після зображення основи позначають вершину піраміди, яку сполучають бічними ребрами з вершинами основи, невидимі ребра зображають штриховими лініями. Для більшої наочності рисунка висоту піраміди зображають «вертикальним відрізком».

Піраміди, в яких бічні ребра нахилені до площини основи під рівними кутами

Якщо в деякій піраміді всі бічні ребра рівні між собою або якщо вони утворюють із площиною основи (чи висотою піраміди) рівні кути, то вершина піраміди проектується в центр кола, описаного навколо основи (схема «Окремі види пірамід»).

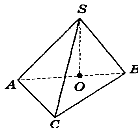
Задача.

В основі піраміди лежить прямокутний трикутник з катетом а і протилежним кутом α. Бічні ребра піраміди утворюють з основою кут β. Знайдіть площу найбільшої бічної грані піраміди.

Розв'язання

Нехай SABC — задана піраміда; <ACB = 90°, <CAB = α , ВС = а; SO(АВС) (рис.) Оскільки <SAO = <SCO = <SBO = β , то точка О — центр кола, описаного навколо трикутника АВС. Оскільки ΔΑΒΟ —прямокутний, то точка О — середина АВ. 

Найбільшою бічною гранню є грань SAB, тоді S_SAB = АВ · SO.

Із ΔАВС АВ = = , тоді АО = .

Із ΔASO SO = AO tg<SAO =.

Отже, S_SAB = · · =

Відповідь. .

Розв'язування задач

1.            В основі піраміди лежить прямокутний трикутник з кутом 30° і протилежним йому катетом, що дорівнює 30 см. Бічні ребра нахилені до площини основи під кутом 60°. Знайдіть висоту піраміди.

              (Відповідь. 30 см.)

2.            В основі піраміди лежить прямокутний трикутник з гіпотенузою 12 см. Знайдіть висоту піраміди, якщо всі бічні ребра нахилені до площини основи під кутом 30°. (Відповідь. 2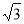см.)

Піраміди, в яких усі двогранні кути при основі рівні між собою

Якщо в деякій піраміді усі двогранні кути при основі рівні між собою, то вершина піраміди проектується в центр кола, вписаного в основу (схема «Окремі види пірамід»).

Крім того, в таких пірамідах висоти бічних граней, проведені з вершини піраміди, рівні і кути, утворені цими висотами з висотою піраміди, рівні.

Розв'язування задач

1.            Основою піраміди є трикутник зі сторонами 13, 20 і 21 см. Знайдіть висоту піраміди, якщо двогранні кути при основі дорівнюють по 30°. (Відповідь. 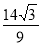см.)
2.            Основою піраміди є прямокутний трикутник з гострим кутом α і катетом b, прилеглим до нього. Кожна бічна грань нахилена до ос­нови піраміди під кутом β. Знайдіть бічну поверхню піраміди. (Відповідь. .)

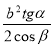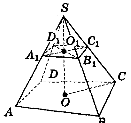Теорема про властивість площини, яка перетинає піраміду і паралельна основі піраміди.

1. Переріз піраміди площиною, яка паралельна до площини

основи, є многокутник, подібний даному: АВСD А₁В₁С₁D₁.

2. Бічні ребра і висота піраміди діляться площиною, яка паралельна до основи піраміди, на пропорційні відрізки:.

3. Площі перерізу і основи піраміди відносяться як квадрати їх відстаней від вершини: .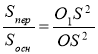

Розв'язування задач

1.          У піраміді проведено переріз паралельно до основи через середину висоти. Площа основи дорівнює S. Знайдіть площу перерізу. (Відповідь. .)
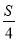2.          У піраміді переріз, паралельний до основи, ділить висоту у відношенні 3 : 4   (в напрямку від вершини до основи), а площа перерізу менша площі основи на 200 см². Знайдіть площу основи. (Відповідь. 245 см².)

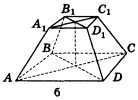
Поняття зрізаної піраміди

Зрізаною пірамідою називається частина піраміди, що обмежена основою і січною площиною, яка паралельна основі.

Демонструються моделі зрізаних пірамід.

Паралельні грані зрізаної піраміди називають її основами, а всі інші — бічними гранями.

Основи зрізаної піраміди — подібні многокутники, їх відповідні сторони попарно паралельні, тому бічні грані зрізаної піраміди — трапеції.

Висотою зрізаної піраміди називають перпендикуляр, проведений із якої-небудь точки однієї основи на площину другої основи. Висотою зрізаної піраміди називають також відстань між площинами її основ.

Переріз площиною, яка проходить через два бічні ребра зрізаної піраміди, які не лежать в одній грані, називається діагональним.

Щоб побудувати зрізану піраміду, спочатку будують повну піраміду, проводять переріз, паралельний основі, а потім зайву верхню частину стирають

IV. Підведення підсумку уроку

Запитання до класу

1) Дайте означення піраміди (основи піраміди, бічних граней, ребер, висоти).

2) Бічні ребра піраміди рівні. У яку точку проектується її вершина?

3) Бічні грані піраміди однаково нахилені до основи. У яку точку основи проектується її вершина?

4) Скільки бічних граней, перпендикулярних до площини основи, може мати піраміда?

V. Домашнє завдання