Урок " Площа прямокутника і квадрата"

Про матеріал

На уроці розв'язуються задачі практичного змісту, які забезпечують краще розуміння учнями фінансових питань ( реалізація наскрізної лінії "Підприємливість і фінансова грамотність").

Перегляд файлу

Шевчук І.В.

Нігинська ЗОШ І-ІІІ ст.

Урок математики в 5класі

Тема. Площа прямокутника і квадрата

Формування компетентностей:
• предметна компетентність: удосконалити вміння обчислювати площу прямокутника та квадрата;

створити умови для усвідомлення учнями цінності практичного застосування формули площі прямокутника у житті,
• ключові компетентності:
• уміння вчитися впродовж життя — прагнути до вдосконалення результатів своєї діяльності;
• спілкування державною мовою — доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень;
• ініціативність і підприємливість — аналізувати, прогнозувати, ухвалювати оптимальні рішення;

Тип уроку: удосконалення вмінь і навичок.

Наочність та обладнання: матеріал для «Доміно », ватман, маркери, таблиці з
               домашнім завданням, кошторисна таблиця, завдання для груп на
               окремих аркушах.
                                                                           Покажи мені – і я запам’ятаю.

Дай мені діяти самому – і я навчуся…

Китайська мудрість

Хід уроку

Організаційний етап

1.Ознайомлення учнів із темою та метою уроку

Я зачитаю акровірш, початкові букви рядків якого підкажуть вам ключове поняття, яке ми будемо використовувати на цьому уроці.

Прямокутник всі ми знаємо,

Легко його зображаємо,

От би точно нам ще взнати,

Щоб його пофарбувати,

А скільки ж фарби купувати?

Так, сьогодні ми з вами продовжуємо вивчати площу прямокутника і квадрата. І ви побачите яку важливу роль відіграє формула площі прямокутника і як знання цієї формули допоможе вам в житті .

Моделювання ситуації у вигляді проблемної задачі

Задача. Наприкінці навчального року в математичному кабінеті потрібно буде зробити косметичний ремонт: пофарбувати підлогу і двері , пофарбувати стелю білою водоемульсійною фарбою, стіни – кольоровою і наклеїти багет на стіни. На батьківських зборах ваші батьки вирішили, що спонсорська допомога батьків з однієї сім`ї не повинна перевищувати 100грн. Використовуючи запропоновані джерела, проведіть розрахунки і підкажіть батькам чи вистачить зібраних грошей. Скільки буде коштувати ремонт, якщо його будуть проводити ваші батьки самі?

ІІ. Перевірка домашнього завдання

Домашнім завданням було, зробивши потрібні вимірювання в математичному кабінеті, заповнити таблиці.
(Учитель перевіряє і коректує розміри в таблицях учнів)

Назва	Розмір (м)
Підлога (стеля)	9×6
Демонстраційний стіл	3×1
Двері	1×2

табл.1

$C:\Users\Illya\Desktop\2016-10-27\267.jpg$ Передня стіна( пофарбована частина)

Назва	Розмір (см)
Над дошкою	400×50
Над дверима	100×50
Справа від дверей	100×200

табл.2

$C:\Users\Illya\Desktop\2016-10-27\269.jpg$ Задня стіна ( пофарбована частина)

Назва	Розмір (см)
Зліва від дверей	100×200
Над дверима	100×50
Справа від дверей	400×100

табл.3

(Справа від дверей висота панелі вища, бо там розміщені вішаки для одягу).

Права стіна (пофарбована частина)

$C:\Users\Illya\Desktop\2016-10-27\263.jpg$

Ліва стіна (пофарбована частина:

Назва	Розмір (м)	Кількість
Права стіна	9×2
Ліва стіна( проміжок між вікнами)	1×2	3

табл.4

$C:\Users\Illya\Desktop\2016-10-27\268.jpg$

ІІІ. Актуалізація опорних знань учнів

Методичний прийом «Доміно ».

На одних аркушах написано початок фраз , на інших – закінчення до них, серед закінчень – не всі правильні. Учням потрібно підібрати правильні закінчення. Все зроблено в двох екземплярах, до демонстраційного стола викликають двох учнів. Хто з учнів виконає завдання швидше, тому на бал вища оцінка.

00 000

10 000

Рівні фігури мають

різні площі

рівні площі

Площа фігури дорівнює

сумі площ її частин

Площа квадрата дорівнює

Площа прямокутника дорівнює

квадрату його сторони

2. Поки 2 учні складають незакінчені фрази, для решти учнів класу усно методичний прийом «Сніжна грудка».

Учитель показує на учня і говорить: «Слово!» Той промовляє слово, яке стосується теми уроку. Показує на іншого учня і говорить : «Речення!». Другий учень складає речення з цим словом. Третій учень придумує запитання з цим словом, а четвертий дає відповідь, можна продовжити: запитання – відповідь…

Наприклад:

Слово	Прямокутник
Речення	Прямокутник – це чотирикутник у якого всі кути прямі і протилежні сторони попарно рівні
Запитання	Яка формула периметра прямокутника?
Відповідь	Р=2а+2b
Запитання	Яка формула площі прямокутника?
Відповідь	S=ab

ІV. Удосконалення вмінь і навичок. Практичне застосування формули площі і периметра прямокутника.

Робота в групах

(клас ділиться на малі групи диференційовано)

Завдання для першої групи (середній рівень)

Задача 1 . Скільки потрібно купити багета, щоб обклеїти стіни. Яка площа стелі (табл.1)?

Розв’язання.

1)Р=2а+2b=2 (а+b)= 2(9+6)=215=30 (м )- потрібно багета;

2) S=a b=96=54() – площа стелі.

Відповідь:30 м ; 54.

Завдання для другої групи (достатній рівень)

Задача 2. Яку площу підлоги математичного кабінету потрібно пофарбувати, якщо під демонстраційним столом підлога не фарбується(табл.1) ?

Розв’язання.

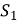=a b=96=54(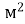) – площа підлоги;
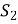=a b=31=3(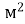) – площа демонстраційного стола;
S = 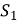-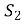=54-3=51(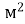) – площа підлоги, яку потрібно пофарбувати.

Відповідь: 51

Завдання для третьої групи (високий рівень)

Задача 3. Яка загальна площа пофарбованої частини стін математичного кабінету (табл.1-4)?

Вказівка . Так. як ми ще не вчили десяткові дроби, то розміри пофарбованої частини передньої і задньої стіни подано в сантиметрах. Тому лише, знайшовши загальну площу фарбування обох стін, одиниці площі переведіть з квадратних сантиметрів в квадратні метри.

Розв’язання.

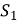=a b=92=18(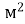) – площа пофарбованої частини правої стіни;
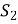=3S=3a b=312=6(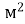) – площа пофарбованої частини лівої стіни;

3)Площі пофарбованої частини передньої і задньої стіни доцільніше обчислювати, заповняючи таблицю:

Назва	Розмір(см)	Площа()
Над дошкою(передня стіна)	400×50	20 000
Над дверима(передня стіна)	100×50	5 000
Справа від дверей (передня стіна)	100×200	20 000
Зліва від дверей(задня стіна)	100×200	20 000
Над дверима(задня стіна)	100×50	5 000
Справа від дверей (задня стіна)	400×100	40 000
Разом		110 000

1=10 000

=110 000=11– площа пофарбованої частини передньої і задньої стіни разом;

S =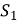++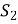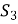=18+6+11=35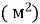– загальна площа пофарбованої частини стін математичного кабінету.

Відповідь: 35.

Фізкультхвилинка

Всі учні разом промовляють і виконують рухи руками:

Із-за парт ми дружно встали

І кути всі показали:

Руки в сторони розвели

Й кут розгорнутий провели.

Праву руку залишаємо,

Ліву – трішки піднімаємо

Знають всі: це кут – тупий,

Який більший за прямий.

             Тепер позицію зміняємо :
             Ліву –в сторону тримаємо,
             Праву руку – рівно вгору:
             Кут прямий дає всім фору.

Праву руку – трішки вліво:

Й гострий кут – усім на диво!
Це вже кожен зрозумів:

Він – найменший із кутів.

Отак просто під час гри

Повторили ми кути:

Кут розгорнутий, прямий,
Навіть гострий і тупий.

3.Колективне розв’язування задачі :

Задача 4. Користуючись одержаними результатами та кошторисною таблицею, обчисліть вартість косметичного ремонту математичного кабінету( для економії часу кінцеві результати підкреслюємо і записуємо на ватмані).

№ з/п	Перелік матеріалів	Одиниці виміру	Ціна за одиницю (грн.)	Витрата
1	Фарба «Снєжка -Ультра»	10л	125.00	10л на 60
2	Фарба «Снєжка -Ультра»	5л	75.00	5л на 30
2	Пігмент «Colorex» №20 персиковий	100мл	15.00
3	Емаль біла «Тріора»	900 г	41.00	100г на 1
4	Емаль для підлоги жовто-коричнева	2 кг 600г	70. 00	100г на 1
5	Розчинник «Eskaro White Spirit»	1л	164.00	1л на 3 кг фарби
6	Багет	2м	24.00
7	Клей	300 г	58.00	300г на 10м багета

Зауваження . В таблиці подано оптові ціни на матеріали.

Розв’язання.

Скільки потрібно коштів на фарбування стін і стелі?

Рекомендація. Стеля і стіни фарбуються тією самою фарбою «Снєжка -Ультра» . Щоб зекономити фарбу доцільно спочатку пофарбувати стелю і до фарби, що залишилася додати пігмент«Colorex» №20персиковий і фарбувати стіни.

1. Яка загальна площа стін і стелі?

35+54= 89).

2.Скільки потрібно фарби?

Якщо розхід фарби 15л на 90, а в нас загальна площа – 89 то зрозуміло, що нам потрібно 15лфарби.

3.Яка вартість 15л фарби «Снєжка -Ультра»?

125+75=200(грн.).

4. Скільки коштуватиме пігмент «Colorex» №20 персиковий, якщо
для насичення кольору нам потрібно 200мл пігменту ( 2 тюбики)?

2 15 =30 (грн.)

5. Скільки потрібно коштів на фарбування стін і стелі?

200+30 = 230 (грн.)

Користуючись табл.1 та кошторисною таблицею, розрахуйте скільки потрібно купити білої емалі «Тріора» для фарбування дверей, якщо в кабінеті 2 дверей (двері фарбувати з двох сторін)? Яка буде вартість емалі?

Яка площа дверей?

1 2=2 ).

Яка загальна площа двох дверей фарбованих з двох сторін?

2 2 2 =8).

Скільки потрібно емалі?

100 8 = 800 (г).

Чи вистачить 1 банки емалі для фарбування дверей?

Так, як 800г 900г, то потрібно купити 1 банку емалі.

Яка вартість 1банки емалі?

141= 41 (грн.).

Скільки потрібно купити банок жовто-коричневої емалі для підлоги? Скільки потрібно коштів?
1) 51 100= 5100 (г) – потрібно емалі.

Міркування:
1 банка емалі важить 2 кг600г =2600г,
2 банки – 5200 г ,

5100г5200 г. Отже, нам потрібно 2 банки емалі.

2) 2 70 = 140 (грн.)

Скільки потрібно купити розчинника?Яка буде вартість?

Міркування:

загальна вага потрібної для фарбування емалі становить :

800+5100=5900(г),

а розхід розчинника:

3кг емалі – 1л розчинника,

6 кг емалі – 2л розчинника

5900г = 5 кг900г, 5кг900г 6 кг.

Отже, нам вистачить 2л розчинника.

2 164 =328 (грн.)

Самостійно:

Скільки буде коштувати багет і клей разом, якщо врахувати, що
1 тюбик клею важить 300г?

Скільки буде коштувати багет?

30: 224 =360 (грн.)

Скільки буде коштувати клей?

1 тюбик клею – 300г, 1 тюбик клею – 10м багета,

30: 1058 =174 (грн.)

3. Скільки буде коштувати багет і клей разом?

360+174= 534 (грн.)

Колективно :

Яка вартість косметичного ремонту математичного кабінету?

230+41+140+328+534 = 1273(грн.)

Висновки:

В 5 класі 13 учнів, тому максимальна спонсорська допомога батьків буде:

13 100 =1300 (грн.)

Так, як вартість косметичного ремонту математичного
кабінету становить 1273грн, то цих грошей вистачить на запланований ремонт при умові:

матеріали закуплять по оптових цінах ( можна батькам об’єднатися на закупку матеріалів разом з батьками з інших класів);
доставку матеріалів батьки здійснять за рахунок спонсора (хтось із батьків);
ремонтні роботи батьки виконають самі.

V. Підсумки уроку

Рефлексія

На уроці я…

– дізнався…

– зрозумів …

навчився..
я не вмів, тепер умію…
на наступному уроці я хочу…

VI. Домашнє завдання

Задача. Підрахуйте вартість ремонту вашої домашньої кімнати. Через який час батьки зможуть зробити вам ремонт кімнати, якщо кожного місяця, починаючи із наступного, будуть відкладати на ремонт 200грн?

docx

Завантажити

Зберегти на потім

Додав(-ла)

Шевчук Інна Володимирівна

Пов’язані теми

Математика, 5 клас, Розробки уроків

Додано

29 лютого 2020

Переглядів

742

Оцінка розробки

Відгуки відсутні