Урок " Початкові відомості про статистику. Способи подання даних та їх обробка".

Тема: Початкові відомості про статистику. Способи подання даних та їх обробка.

Мета: формування компетентностей.

Предметна: формувати уявлення про статистику як науку, її методи та характеристики.

Ключові: уміння розуміти й перетворювати тексти математичних задач, аргументувати, доводити правильність тверджень.

Інформаційна-цифрова: уміння структурувати дані, діяти за алгоритмом та складати алгоритм.

Основні компетентності у природничих науках: усвідомлення важливості математики як універсальної мови науки, техніки.

Хід уроку

1. Перевірка домашнього завдання. Актуалізація знань.

• Які правила, формули використовували під час виконання домашнього завдання?
• Яка подія називається випадковою, вірогідною, неможливою?

Дискусія на тему:  «Чому статистика як суспільна наука вивчає природу, навколишнє середовище, техніку і технічний прогрес?”

 Способи подання даних та їх обробка має декілька етапів.

Зведення – етап статистичного дослідження, який представляє собою систематизацію та класифікацію статистичного матеріалу, отриманого у результаті статистичного спостереження

Основною базою статистичного зведення є групування

Групування – розподіл сукупностей на групи, однорідні за якою будь ознакою. Різниця між максимальним та мінімальним значенням ознаки кожної групи називається інтервалом.

Інтервали бувають

•                                рівні
•                                нерівні

Важливе значення має графічне зображення статистичної інформації. Правильно побудований графік робить статистичну інформацію більш виразною, вона краще запам'ятовується й зручно сприймається. Наприклад, у  вигляді стовпчастої діаграми, ще називають її гістограмою.

3. Відпрацювання вмінь та навичок.

Розглянемо задачу, за допомогою якої покажемо  графічно ряд розподілення приватних шкіл за кількістю учнів.

Задача 1

Відомі наступні дані про кількість учнів в 40 приватних шкіл.

Побудуйте за цими даними  ряд розподілення шкіл за кількістю учнів. Виділити 5 груп. Показати ряд графічно:

•                                гістограма

            Гістограма – графічне зображення інтервального варіаційного ряду

На осі абсцис відкладають значення ознаки – інтервали, а по осі ординат частоти.

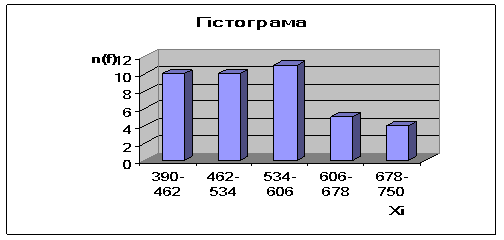
Розглянемо приклад з розрахунком відносної величини на прикладі задачі.

                                                                          Задача

По регіону є наступні про введення в експлуатацію жилої площі

Визначити:

1.                динаміку введення в експлуатацію жилої площі по кожному виду жилих будинків, та в цілому по регіону
2.                структуру введеної в експлуатацію жилої площі в минулому та звітному роках.
3.                структуру введеної в експлуатацію площі зобразити на графіку

Рішення

Показники динаміки (темп росту) наступні, %

Цеглинні дома Тр = У₁ / У₀ = 4200 / 4400 = 0,955 відносна величина або 95,5%

Панельні дома Тр = 2100 / 2800 = 0,75 відносна величина або 75,0%

Котеджі   Тр = 2100 / 800 = 2,625 відносна величина або 262,5%

Структура введеної в експлуатацію жилої площі по регіону представлена у таблиці

Структура введеної в експлуатацію жилої площі по регіону

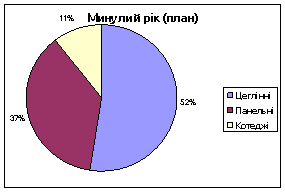
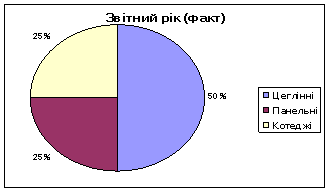
Мал.1 Структура введеної в експлуатацію жилої площі по видам домів у регіоні

Розглянемо, коли зустрічається частота тобто число повторювань, на прикладі задачі.

Задача №2

У наявності є наступні дані про участь в олімпіаді з математики 60 учнів 5,4,2,1,6,3,3,4,3,2,2,5,6,4,3,5,4,1,2,3,3,4,1,6,5,1,3,4,3,5,4,3,3,4,6,4,4,3,4,3,3,4,6,3,5,4,5,3,3,3,4,4,5,4,3,2,5,4,2,3.

Побудуйте за цими даними: ряд розподілу учнів за кількістю разів приймання участі в олімпіаді.

1. Побудуемо ранжирований ряд

1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,6,6,6,6,6.

2. Будуємо  ряд розподілу учнів за кількістю разів приймання участі в олімпіаді.

Однією з кількісних характеристик статистичних закономірностей є середня величина, яка здатна відобразити характерний рівень ознаки, притаманної усім елементам сукупності.

Середня арифметична проста визначається діленням суми значень ознак на кількість значень

Х=Σ х_і/n

де  n- кількість значень ознаки

Наприклад: середня арифметична проста

(дитини)

Крім об’ємних середніх в статистиці використовуються структурні середні (мода і медіана). При проведенні аналізу і характеристики статистичних рядів розраховують моду і медіану. Для дискретних рядів розподілу

Мода - величина ознаки, яка найчастіше зустрічається у даній сукупності.

У варіаційному ряду модою є варіанта, яка найчастіше зустрічається у даному варіаційному ряду.

У даному прикладі мода Мо = 3                             

Медіаною називається - варіанта, яка ділить чисельність упорядкованого ряду, тобто побудованого порядку зростання або зниження варіюючої ознаки, на дві рівні частини. Медіана - це варіанта, яка припадає на середину варіаційного ряду. Наприклад заробіток за день кожного із 5 робітників склав відповідно (грн).

6,0   6,5   7,0   7,4   8,0               Ме=7

Робота з підручником.

Алгебра 9 клас А.Г.Мерзляк с. 243 №24.1., №24.7.

4. Підсумок уроку.

Статистичні дані мають широкий спектр використання. Від допомоги компаніям зрозуміти смаки споживачів до аналізу клінічних досліджень. Знання статистики дає можливість грамотно аналізувати: склад і параметри товарів та послуг, вплив інфляції на ціни й на доходи, цінові пропозиції тощо. Без статистичних даних неможливе управління державою, розвиток економіки і культури, розробка програм розвитку країни.

 Висновок:

Статистика допомагає зрозуміти навколишній світ. Вона широко використовується у повсякденному житті. Завдяки статичним даним можна завжди проаналізувати ситуацію, порівняти її з іншими, прийняти рішення, провести наукові дослідження.
Знання статистики дає очевидні переваги на ринку праці. В останні 25 років володіння статистикою стало однією з ключових вимог до претендентів на вакансії у великих компаніях.

5. Домашнє завдання.

С.244  №24.6., № 24.8.