Урок "Подібні трикутники"

Тема. Подібні трикутники.(урок формування компетентностей)

 Цілі: Почати формувати компетентності та навики учнів з теми, розвивати навики колективної роботи у поєднанні із самостійною; формувати комунікативну, соціальну, функціональну компетентності; формування вміння використовувати власний досвід, організовувати свою роботу.

Тип уроку: урок формування компетентностей.

Перебіг уроку

1. Організаційний момент.
2. Перевірка домашнього завдання. (усний коментар)№384,408,

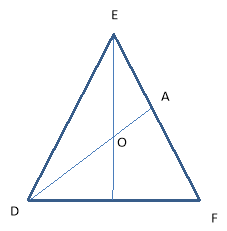
3. Актуалізація опорних знань та навичок(кросворд):

1.Давньогрецький учений, засновник мілетської школи.

         2. Назва відрізків,  відношення довжин яких рівні.
         3.Перетинаються в одній точці, яка ділить кожну з них у відношенні 2:1.

         4. Відрізок, який ділить кут трикутника навпіл.

         5. Розділ геометрії, у якому вивчають трикутник.

         6. Трикутники, які можна сумістити накладанням.

         7.Твердження,  за допомогою яких доводимо рівність трикутників.

4.  Повідомлення теми і мети уроку.

Перш, ніж оголосити тему уроку пропоную переглянути коротеньке відео.

У повсякденному житті ви часто стикаєтесь з об’єктами, які мають однакову форму, але різні розміри. Геометричні фігури, які мають однакову форму, називають подібними. Сьогодні ми з вами розпочинаємо вивчення однієї з найцікавіших тем геометрії «Подібність трикутників». Чому найцікавіших? Бо знання з  цієї теми допомагають в найнесподіваніші моменти

5. Подача матеріалу

• Означення подібних трикутників.(Демонстрація картонних моделей подібних трикутників)

• Лема про подібні трикутники

- Лему про подібні трикутники часто застосовують для вимірювання висоти недосяжного предмета. Зараз і ми спробуємо це проробити. Але спершу послухаємо інформацію про спосіб Фалеса Мілетського для такого  вимірювання.

6. Застосування знань, умінь та навичок

      Спосіб Фалеса Мілетського для вимірювання висоти недосяжних предметів

Історія розповідає про те, як, мандруючи Єгиптом, Фалес був вражений величчю піраміди Хеопса.

- Скажіть, будь ласка, а яку висоту вона має? – запитав він жерців.

- О, це дано знати хіба що Богу Сонця Ра, а не людині, - відповіли жерці.

- Зачекайте хвилиночку, зараз я точно підрахую висоту піраміди!- запевнив їх Фалес.

 Він вийшов від проміння Сонця і виміряв довжину своєї тіні. Скажімо, тінь була вдвічі довшою за зріст Фалеса . Із цього Фалес зробив висновок, що в цю мить предмети мають тінь удвічі більшу за  них самих. Тож залишається обчислити довжину тіні піраміди Хеопса.

Якщо ви вважаєте, що жерці були в захваті від розуму та винахідливості Фалеса, то ви помиляєтесь. Навпаки, вони дуже обурилися. Те, що на їхню думку, людині не дано пізнати, якийсь там грек з Мілета обчислив майже миттєво!.. Ні, таке не пробачають! І жерці вирішили вбити Фалеса. На щастя, один із них виявився порядною людиною і підказав Фалесу скоріше сідати на корабель, який ось-ось мав відпливти до Єгипту…

1.               Задача вимірювання висоти недосяжного предмета.(учні- експерти виконують заміри , учні класу записують і виконують завдання)

     Завдання: виміряти висоту щогли корабля, зображеного на плакаті.

     Спосіб вимірювання:за допомогою записника і олівця і шнурка.

                                                ХІД РОБОТИ

1. Займіть зручну для вимірювання позицію, тобто так, щоб об’єкт було добре видно.
2. Виставте записник так, щоб його верхня частина була на рівні очей. Олівець тримайте так, щоб найвища його точка збіглася з верхньою частиною об’єкта.

3. Виміряйте відстань ОС між оком і записником, ОС=___________  см.

4. Виміряйте відстань КD від зайнятої позиції до об’єкта, висоту якого вимірюєте.

    КD=_______________  см.

5. Виміряйте відстань ВС висоту видимої частини олівця, ВС=__________  см.

6. Трикутники _____________і ____________ подібні за ____________________

____________________________________________________________________

7. Якщо трикутники подібні, то їх відповідні сторони_______________________

8. Запишіть, які сторони трикутників пропорційні:_________________________

9. АМ=     ___________________    =     _________________см.

- Відомий французький письменник Жуль Верн написав чудовий роман «Таємничий острів», де також схожим способом описано вимірювання висоти гранітної скелі.

Поки що найголовніше завдання полягало в тому, щоб визначити, як далеко перебуває острів від заселеної землі, що й мало бути зроблено того ж дня, якщо дасть змогу погода.

Тепер належало доповнити вчорашні спостереження новими даними, вимірявши висоту плоскогір'я Широкий Обрій над рівнем моря.

Герберт, маючи невтоленну жадобу до знань, пішов слідом за інженером, а той відійшов од гранітної кручі аж до води край берега. Сайрес Сміт прихопив із собою пряму жердину завдовжки футів дванадцять, вимірявши її так точно, як тільки міг, за власним зростом, який знав достеменно, до міліметра.

Зупинившись кроків За двадцять від краю моря і футів за п'ятсот від гранітної кручі, що зводилася перпендикулярно до водної гладі, Сайрес Сміт застромив жердину на два фути в пісок і за допомогою виска старанно виставив її перпендикулярно до лінії обрію.

Після цього він одійшов і ліг на землю на такій відстані, щоб у полі його зору перебував верхній кінець жердини та гребінь гранітної кручі, й старанно позначив це місце на піску кілочком. Потім, звертаючись до Герберта, інженер запитав:

- Ти не забув іще Основ геометрії?

- Ще трохи пам'ятаю, пане Сайресе, - обережно, аби не перехвалити себе, відповів Герберт.

- Пам'ятаєш властивості двох подібних трикутників?

- Авжеж, - відповів хлопець. - У двох подібних трикутників відповідні сторони пропорційні одна одній.

- Отож, синку, я щойно побудував два подібних трикутники, обидва прямокутні: один менший, сторонами якого будуть жердина, встромлена перпендикулярно в пісок, і пряма, рівна відстані від нижнього кінця жердини до кілочка, а гіпотенузою - мій промінь зору; у другого трикутника сторонами є прямовисна лінія гранітної кручі, яку нам треба виміряти, і відстань од кілочка до підошви стіни, а гіпотенузою - знову ж таки мій промінь зору, тобто продовження гіпотенузи першого трикутника.

- О, пане Сайресе, я зрозумів! - вигукнув Герберт. - Відстань од кілочка до жердини пропорційна відстані од кілочка до підошви стіни, а висота жердини пропорційна висоті стіни.

- Саме так, Герберте, - відповів інженер. - І коли ми виміряємо обидві відстані од кілочка, то, знаючи висоту жердини, швидко розв'яжемо пропорцію і таким чином дізнаємось, яка висота кручі, позбувшися мороки міряти її безпосередньо.

2. Задача. Уявіть собі, що ви вирушили у похід. Попереду- пригоди, перешкоди, які потрібно буде вам подолати, щоб дістатися кінцевої точки вашого маршруту.

  Знайти відстань між двома об’єктами А і В, до яких можна підійти, але між якими знаходиться перешкода.  АС=6м, СМ=4м, СN= 9м, МN=8м.

3. Усні вправи

1)Чи подібні трикутники, якщо  А=А₁=60, В=70,  В₁=80, С=50,  С₁=40 ?

2) Дано подібні трикутники. Знайти оефіцієнт подібності, якщо відповідні сторони цих трикутників дорівнюють 24см і 8 см.

3) Сторони трикутника АВС дорівнюють 6см, 8см, 7см. Знайти відповідні сторони подібного йому трикутника, якщо А₁В₁:АВ=2

4) Сторони трикутника А₁В₁С₁ дорівнюють 18см, 21см, 24см. Знайти відповідні сторони подібного йому трикутника, якщо А₁В₁:АВ=2

VІІ. Підсумок уроку і рефлексія

Отримали уявлення про подібність геометричних фігур, засвоїли означення подібних трикутників , вчились знаходити елементи подібних трикутників та застосовувати набуті знання на практиці.

 Думаю, що тему ви засвоїли добре. То ж оцініть свою працю:

- Я вмію творчо працювати. Це мені подобається.

- Я задоволений, що можу так працювати на уроці.

- Я почував себе не дуже впевнено.

VІIІ. Домашнє завдання:

Вивчити п.12

Виконати:№ 427, 432