Урок "Правильна піраміда та її елементи. Розв’язування задач".

Тема заняття :  Правильна піраміда та її елементи.

                               Розв’язування задач.

Тривалість:  90 хв.
Мета заняття:
Навчальна:

 формувати  поняття «правильна піраміда», «апофема піраміди»; вивчити властивості правильної піраміди і теорему про знаходження бічної поверхні правильної піраміди; створити умови для дослідження і аналізу ситуації з метою набуття нових знань; застосовувати вивчені властивості правильної піраміди для розв’язування конкретних завдань.
Розвиваюча:

розвивати пам'ять і мислення, просторову уяву; розвивати цікавість до математики, прагнення краще вчити предмет; здатність до творчого застосування знань і вдосконалення умінь. 
Виховна:

виховувати наполегливість і відповідальність, допитливість, уважність, натхнення, любов до навчання та вміння працювати разом, виховувати акуратність при побудові малюнків.

Обладнання: підручник, мультимедійний проектор, презентація, моделі многогранників, таблиця «Піраміда», роздатковий матеріал.

Тип заняття – формування нових знань

 

Епіграф заняття:

 

Знання можуть бути купою каміння,

Що задушило особистість.

І знання можуть бути вершиною піраміди,

На якій стоїть особистість.

                               Валентин Розов

 

Структура:

№	Назва етапу	Тривалість
1.	Організаційний момент	2 хв
2.	Актуалізація опорних знань. Домашнє завдання. Усне опитування.	19 хв
3.	Сприймання і усвідомлення нового матеріалу	25 хв
4.	Закріплення нового матеріалу	23 хв
5.	Самостійна робота	12 хв
6.	Домашнє завдання	2 хв
7.	Підведення підсумків	7 хв

 

 

 

    

    Хід заняття

1. Організаційний момент.

( Перевірка присутності студентів, наявність форми одягу).

2. Актуалізація опорних знань.

    Перевірка домашнього  завдання.

Обговорення розв'язування домашніх задач № 1, 2.  Правильність виконання домашнього завдання перевіряю за записа­ми, розміщеними на екрані.

Задача №1.

В основі піраміди лежить прямокутний трикутник з катетом 6 см і гіпотенузою 12 см. Знайдіть обєм піраміди , якщо всі бічні ребра нахилені до площини основи під кутом 30°.

 

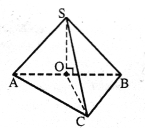Розв’язання.

= 90°, АВ = 12 см, АС = 6см. Оскільки = = = 30°, = (за катетом і гострим кутом), звідки ОА = ОВ = ОС. Тому О – центр кола, описаного навколо , тобто О середина гіпотенузи. ОА = 6 см. З : Н = = 2 cм.

СВ = cм. = ().

V = ().

Відповідь : .

 

Задача №2.

Основою  піраміди є прямокутник зі соронами 6 см і 15 см. Висота піраміди дорівнює 4 см і проходить через точку перетину діагоналей основи. Знайдіть площу бічної поверхні піраміди.

Розв’язання.

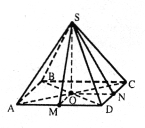АВ = 6 см, АD = 15 см, = 4 см. ОN = АD = 7,5 см; ОМ = АВ = 3 см.

SN = = 8,5 см; SМ = = 5 см. = 2 + 2 = CD = 126 .

Відповідь : .

 

 

 

 

 

 

 

 

Усне опитування.

Інтерактивна  вправа « Закінчи речення» .
(Студенти усно продовжують речення.)
1). Тіла, поверхні яких складаються зі скінченного числа плоских многокутників     

     називаються … (Многогранники).
2). Многогранник, який складається з плоского многокутника, точки, яка не  

     лежить у площині плоского многокутника і всіх відрізків, що сполучають цю  

     точку з точками плоского многокутника називається… ( пірамідою ).
3). Точка, яка не лежить у площині основи піраміди називається…
     ( вершиною піраміди ).
4). Відрізки, що сполучають вершину піраміди з вершинами основи,  

     називаються… ( бічними ребрами).
5). Загальна частина площини і поверхні опуклого многогранника … (Грань).
6). Кожна бічна грань піраміди є… ( трикутник ).
7). Перпендикуляр, опущений з вершини піраміди на площину основи  

     називається… ( висотою піраміди ).

8). Суму площ усіх бічних граней піраміди називають … (площею бічної 

    поверхні пі­раміди).

9). Суму площ усіх бічних граней піраміди  та площі основи називають … 

    (площею повної поверхні пі­раміди).

10). Многокутник  називається правильним, якщо … (в нього всі сторони рівні 

     й усі кути рівні).
11). Центром правильного многокутника називають… (центр описаного  

    навколо нього (або вписаного в нього) кола).

12). Центр правильного трикутника лежить… (в точці перетину медіан, 

    бісектрис, висот).

13). Центр квадрата лежить … (в точці перетину діагоналей).

14). Центр правильного  шестикутника лежить … (в точці перетину 

    діагоналей).

3. Сприймання і усвідомлення нового матеріалу.

 - Сьогодні ми з вами будемо працювати у  малих групах, які створили на попередньому занятті. Це групи «Історики», «Дослідники» і «Практики». Принципи роботи у групах наступні .
Принцип 1. Поважай думки товаришів з групи, не насміхайся і не критикуй.
Принцип 2. Зусилля кожного студента потрібні і незамінні для успіху всієї групи.
Спікерами будуть   Касьян Софія, Новосільська Ірина, Паламар Олеся, вони і розприділять ролі між учасниками групи. (На столах у вас є листки обліку роботи групи, де секретар буде робити відмітки про виконану роботу кожного студента).

 Мотивація навчання та повідомлення теми і мети заняття.

 Наступним етапом нашого заняття буде розв’язування кросвордів. Кожна група має окреме завдання (завдання у кожної групи на столі.)

• Які ключові слова кожна група знайшла?  

Відповідь: многогранник, піраміда, правильна.

Отже, тема сьогоднішнього заняття:  Правильна піраміда та її елементи. Розв’язування задач. 

Мета заняття:

• формувати вміння  знаходити невідомі  елементи, площі поверхні правильної піраміди; 
•  розвивати просторову уяву, культуру    математичного мовлення;
• повторити співвідношення між елементами   прямокутного трикутника.

Епіграфом нашого заняття ми взяли слова Валентина Розова:

Знання можуть бути купою каміння,

Що задушило особистість.

І знання можуть бути вершиною піраміди,

На якій стоїть особистість.

 Суть епіграфа розкриє поезія «Піраміда»

 

Життя будує з цегли піраміди,

Де цегла – кожен з поміж нас.

Це ті, хто знає місце Атлантиди

Або ж оті, яких вбиває час …

 

Та в піраміді все нестало, хаотично

І доля рухає цеглини між рядами,

Ти можеш впасти донизу …Критично!

Або ж блистіти у промінні слави…

 

І піраміда ця – весь сенс життя,

Де кожна цегла буде головною,

Яка формує суть буття

Що весь мільйон керується одною…

 

Зв’язки людські, неначе блоки

Їх не єднає океан бетону,

А єдність – то зустрічні кроки,

Й рука простягнута забутому самому…

  Піраміди здавна вважалися одним із семи чудес світу. Араби склали приказку: «Все на світі боїться часу, але час боїться пірамід».  Отже, ми відправляємося у подорож цікавим світом математики, де існують загадкові піраміди. Дороговказом нам стануть слова найвідомішого вченого давніх віків – Піфагора: «Не роби ніколи того, що не знаєш.
Але вчись усьому, що потрібно знати,  і тоді будеш вести   спокійне життя».
  На попередньому занятті ви одержали творче завдання підготувати проекти: «Піраміди Стародавнього світу» , «Піраміди навколо нас», «Піраміди в медицині».  Це завдання ви виконували в малих групах, надаю слово представникам групи «Історики» (проект «Все на світі боїться часу, але час боїться пірамід»)

  - Безумовно, про єгипетські піраміди можна говорити неперервно, та повернімося до математичної точки зору на піраміди.

 Правильною пірамідою називається піраміда, в основі якої лежить правильний многокутник, а основа висоти піраміди збігається з центром цього многокутника.

РАВСD — правильна чотирикутна піраміда.

Тоді за означенням її основа АВСD — правильний чотирикутник квадрат); центр квадрата точка О — основа висоти РО піраміди.               Пряма, яка містить висоту піраміди, називається віссю правильної піраміди. Висота Р0 — вісь правильної піраміди РАВСD.

Побудова правильних пірамід.  

              Для зображення просторових фігур на площині користуються методом паралельного проектування. Зображення піраміди потрібно починати із зображення її основи. Виконуючи зображення фігур, треба дотримуватись правил і вимог креслення. Використовувати суцільні та пунктирні лінії. Зображення повинні бути правильними, повними, наочними і простими у виконанні. Пра­вила зображення многокутників нам відомі. Згадаємо їх.

1) Що є зображенням рівностороннього  трикутника? (Довільний трикутник).

2) Що є зображенням квадрата? (Паралелограм).

3) Що є зображенням правильного шестикутника? (Шестикутник).

- Побудуємо спочатку найпростішу – чотирикутну піраміду. Оскільки піраміда правильна чотирикутна, то в основі лежить квадрат. Зображенням квадрата є довільний паралелограм.  Побудуємо паралелограм АВСД. Центр квадрата – точка перетину діагоналей. Тому побудуємо на зображенні діагоналі АС і ВД, які перетнуться в точці О. Одержимо: точка О  - центр квадрата. Через точку  О проведемо перпендикуляр  ОР до площини (АВСД). Точку Р з’єднаємо з вершинами  А, В, С, Д.Правильна чотирикутна піраміда РАВСД побудована .

- Часто зустрічається ще й трикутна піраміда. Побудуємо її.

Зобразимо основу піраміди – довільний трикутник. Оскільки піраміда правильна, то в основі лежить рівносторонній трикутник. Центр правильного трикутника – точка перетину його медіан. Тому побудуємо медіани АК і СМ на зображенні. Вони  перетнуться в точці О – центрі правильного  трикутника АВС. Через точку  О проведемо перпендикуляр  ОP до площини (АВС) . Точку P з’єднаємо з вершинами  А, В, С. Правильна трикутна піраміда PАВС побудована.

• Більш складною є шестикутна піраміда. Будуємо її.

Основою піраміди є правильний шестикутник. Побудуємо його. Для цього зобразимо ромб у вигляді довільного паралелограма.  А тепер побудуємо симетричний йому ромб відносно однієї із вершин. З’єднаємо точки між собою. Одержимо шестикутник АВСДЕF. Через точку  О проведемо перпендикуляр  ОP до площини шестикутника . Точку P з’єднаємо з вершинами  А, В, С, Д, Е, F. Правильна шестикутна піраміда PАВСДЕF побудована.

- Висота бічної грані називається апофемою.

- Проведемо апофему в трикутній, чотирикутній, та шестикутній правильних пірамідах, які ми з вами побудували.

- Бічні грані в правильній піраміді є рівнобедрені трикутники бічні сторони яких – це бічні ребра, а основа – сторона основи. Тому для побудови апофеми потрібно сторону основи поділити пополам і одержану точку з’єднати з вершиною.

 - Тепер сформулюємо наступні властивості правильної піраміди.

  У правильній піраміди:

- бічні ребра рівні;

- бічні грані рівні рівнобедрені трикутники;

- кути нахилу бічних ребер до площини основи рівні;

- кути нахилу бічних граней до площини основи рівні;

- апофеми рівні .

- Як знайти бічну поверхню правильної піраміди, якщо відомі апофема і сторона основи?
Відповідь. Всі грані піраміди – однакові рівнобедрені трикутники. Площа бічної поверхні піраміди буде дорівнювати площі одного трикутника помноженій на кількість граней  = n   =   =   .
- Отже, площа бічної поверхні правильної піраміди дорівнює півдобутку периметра основи на апофему.
- Як знайти площу всієї поверхні піраміди?

Відповідь. Треба до площі  її бічної поверхні додати  площу основи. 
- Для кращого засвоєння матеріалу у вас на столах є опорні конспекти.
4. Закріплення нового матеріалу

 А зараз повторимо з вами формули для обчислення площ многокутників, довжини сторін, радіуса описаного навколо  многокутника кола та радіуса вписаного в многокутник кола, теорему Піфагора. Для цього проведемо інтерактивну вправу «Хто швидше?» Суть її полягає в тому, щоб знайти помилки у математичних формулах, якщо вони є і у відведену графу записати правильну відповідь (Додаток №№ 1 – 6). Представники якої групи швидше і правильно  виконають завдання, ті наберуть  і найбільшу кількість балів.

Задача. Апофема правильної чотирикутної піраміди дорівнює см, а кут між бічною гранню  і площиною основи 60°. Знайдіть:

1. висоту піраміди ;
2.  довжину сторони основи;
3. площу бічної поверхні піраміди;
4. площу повної поверхні піраміди.

• Що є кутом між бічною гранню і площиною основи і як його побудувати?

Відповідь: Кутом між бічною гранню і площиною основи є лінійний кут двогранного кута. Щоб його побудувати проведемо апофему РН. РО ⊥ (АВСД), НО – проекція РН на площину основи (АВСД).  За теоремою про три перпендикуляри НО ⊥СД.  ∠РНО – це лінійний кут двогранного кута і за умовою дорівнює 60°. (Студент на малюнку, який є на дошці будує кут).

• Що спочатку будемо знаходити і як ?

Відповідь:   Знайдемо сторону основи .  ∆ РОН прямокутний.

∠РНО = 60°. За теоремою про суму внутрішніх кутів трикутника ∠ОРН = 30°.  А катет, який лежить проти кута 30° = дорівнює половині гіпотенузи, тому ОН дорівнює половині РН і дорівнює см. Оскільки в основі лежить квадрат, то сторона основи дорівнює двом ОН.

• Як знайти висоту піраміди?

Відповідь:  З  ∆ РОН за теоремою Піфагора визначимо РО.

• Як  знайти площу бічної поверхні піраміди?

Відповідь: площа бічної поверхні правильної піраміди дорівнює півдобутку периметра основи на апофему. Знайдемо периметр основи тобто квадрата довжину сторони основи помножимо на 4, апофему ми маємо , підставимо у формулу і обчислимо.

• Як знайти площу повної поверхні?

Відповідь: до площі  її бічної поверхні додати  площу основи.  Площу основи обчислимо за формулою S = .

• А тепер запишемо розв’язування  задачі на дошці.

Розв’язання.

 

Дано:  РАВСД – правильна чотирикутна піраміда, апофема РН = см,

            = 60°

Знайти: РО, АД, , 

 

 

 

З ∆РОН  (, ∠РНО = 60°)  ОН = РН =   (см).

АД = 2ОН = 2 = (см).

За теоремою Піфагора  РО = = = = = = 1,5 (см). 

= 4 (см), =   4   = 6 ().

=   = 3 (). = 6 + 3 = 9).

Відповідь: 1,5 см; см; 6 ; 9.  

Задача. Кожна група має правильну піраміду трикутну, чотирикутну і шестикутну. Потрібно виміряти необхідні розміри і знайти площу бічної і повної поверхні, розв’язки  записати на дошці.

Група «Історики». Довжина сторони основи 7 см, апофема 20 см.

= 4 7 = 280 = 7 + 280 = 329

Група «Дослідники». Довжина сторони основи 8 см, апофема 19 см.

= 3 8 = 228 = + 228 = 27,2 + 228 = 255,2

Група «Практики». Довжина сторони основи 3 см, апофема 15 см.

= 3 6 = 135   a = = 3 см.   = = 6 = 23,4 + 135 = 158,4

 - А тепер я пропоную вам послухати повідомлення групи «Дослідники». Під час роботи над проектом  студенти  намагалися з’ясувати, чи має сьогоднішня наша тема «Піраміди» зв'язок з життям? Чи потрібно її вивчати? Проект «Піраміди навколо нас».

- Ми ознайомилися з використанням пірамід у різних сферах людської діяльності. А зараз про «Піраміди в медицині.» Проект групи «Практики».

- На закріплення вивченого матеріалу проведемо самостійну роботу у вигляді тестів.

5. Самостійна робота (Тести).

6. Домашнє завдання.  Вивчити Г.П.Бевз, В.Г.Бевз Алгебра 11

Розділ 6 29, розв’язати вправи №№ 942, 943, 947.
7. Підведення підсумків заняття. 

 - Проаналізуйте свою роботу на занятті, прослухавши притчу. «Йшов мудрець, а назустріч йому три людини, які везли під гарячим сонцем візки з каменями для будівництва. Мудрець зупинився і задав кожному запитання. У першого запитав: «Що ти робив цілий день?» І той з усмішкою відповів, що цілий день возив кляті камені. У другого запитав: «А що ти робив цілий день?»  І той відповів: «Я сумлінно виконував свою роботу». А третій посміхнувся, його обличчя засвітилося радістю і задоволенням: « А я брав участь в будівництві храму!» А що ж на занятті робили ви? Порівняй свої знання на початку і в кінці заняття і дайте відповіді на запитання:
-  Чи отримали ви задоволення від власної праці?
-  Який етап діяльності був найцікавішим? 

Метод «Мікрофон» (доповідають секретарі з кожної групи).

- Надіюсь , що сьогоднішнє заняття принесе вам знання , перефразовуючи епіграф , які  будуть не купою каміння, що задушило особистість, а вершиною піраміди, на якій стоїть особистість.

 

 

 

 

 

Кросворд групи «Історики» ( ключове слово МНОГОГРАННИК).

1. Розділ геометрії, у якому вивчаються фігури  у просторі (Стереометрія).

2. Відношення прилеглого катета до гіпотенузи (Косинус).

3. Сторона грані призми (Ребро.)

4. Відрізок, який сполучає дві вершини призми, що не належать одній грані називається (Діагональ).

5. Твердження, яке доводять називають (Теорема).

6.Відношення протилежного катета до прилеглого називається (Тангенс).

7. Основна геометрична фігура (Пряма).

8. Прямокутник, у якого всі сторони рівні (Квадрат).

9. Елемент піраміди (Вершина).

10. Найбільша сторона прямокутного трикутника (Гіпотенуза).

11. Перпендикуляр, опущений з вершини піраміди на площину її основи, називають (Висота.)

12. Твердження, які містять формулювання основних властивостей найпростіших фігур і не доводяться називаються (Аксіома).

Кросворд групи «Дослідники» (ключове слово ПРАВИЛЬНА).

1. Многогранник (Паралелепіпед).

2. Чотирикутник (Паралелограм).

3. Прямокутник, у якого всі сторонни рівні (Квадрат).

4. Трикутник, у якого всі сторонни рівні (Рівносторонній).

5. Перпендикуляр, опущений з вершини піраміди на площину її основи, називають (Висота).

6. Слово «геометрія» - грецьке, у перекладі на українську означає…(Землемірство)

7. Прямі, які лежать в одній площині і не перетинаються називаються…(Паралельні).

8. Відношення протилежного катета до гіпотенузи (Синус).

9. У прямокутному трикутнику справджується теорема давньогрецького ученого (Піфагор).

 

 

Кросворд групи «Практики» (ключове слово ПІРАМІДА).

1. Одне із семи чудес світу піраміда (Хеопса).

2. Трикутник, у якого дві сторони рівні називається (Рівнобедрений).

3. Розділ геометрії, у якому вивчаються фігури у просторі (Стереометрія).

4. Кут утворений двома площинами із спільною прямою (Двогранний).

5. Слово «геометрія» - грецьке, у перекладі на українську означає…(Землемірство).

6. Давньогрецький учений (Піфагор).

7. Книга для занять з будь-якого предмету (Підручник).

8. Елемент піраміди (Вершина).

 

 

 

 

 

          Додаток № 1.

Завдання для групи «Історики».

№ з/п	Назва формули	Формула	Правильна відповідь
1.	Теорема Піфагора
2.	Площа квадрата	S =
3.	Площа рівностороннього трикутника	S =
4.	Формула Герона	S =
5.	Радіус кола, описаного навколо трикутника	R =
6.	Радіус кола, описаного навколо правильного трикутника	R =
7.	Радіус кола, вписаного в  правильний трикутник	r =
8.	Радіус кола, вписаного в  квадрат	r =
9.	Радіус кола, описаного навколо правильного шестикутника	R =
10.	Радіус кола, вписаного в  правильний шестикутник	r =
11.	Довжина сторони правильного шестикутника	a = R
12.	Довжина сторони квадрата	a = 4r

 

 

                      

 

 

 

 

                      Додаток № 2.

Завдання для групи «Дослідники».

№ з/п	Назва формули	Формула	Правильна відповідь
1.	Теорема Піфагора
2.	Площа квадрата	S =
3.	Площа рівностороннього трикутника	S =
4.	Формула Герона	S =
5.	Довжина сторони правильного трикутника	a = 2r
6.	Радіус кола, описаного навколо правильного трикутника	R =
7.	Радіус кола, вписаного в  правильний трикутник	r =
8.	Радіус кола, вписаного в  квадрат	r =
9.	Радіус кола, описаного навколо правильного шестикутника	R =
10.	Радіус кола, вписаного в  правильний шестикутник	r =
11.	Довжина сторони правильного шестикутника	a =
12.	Довжина сторони квадрата	a = R

 

 

 

 

 

 

 

                      Додаток № 3.

Завдання для групи «Практики».

№ з/п	Назва формули	Формула	Правильна відповідь
1.	Довжина сторони правильного трикутника	a = 4r
2.	Площа квадрата	S =
3.	Площа рівностороннього трикутника	S =
4.	Формула Герона	S =
5.	Довжина сторони квадрата	a = R
6.	Радіус кола, описаного навколо правильного трикутника	R =
7.	Радіус кола, вписаного в  квадрат	r =
8.	Радіус кола, вписаного в  правильний трикутник	r =
9.	Радіус кола, описаного навколо правильного шестикутника	R =
10.	Радіус кола, вписаного в  правильний шестикутник	r =
11.	Довжина сторони правильного шестикутника	a =
12.	Довжина сторони квадрата	a = 2r

 

 

 

 

 

 

 

                      Додаток № 4

Відповіді групи «Історики».

№ з/п	Назва формули	Формула	Правильна відповідь
1.	Теорема Піфагора
2.	Площа квадрата	S =	+
3.	Площа рівностороннього трикутника	S =	S =
4.	Формула Герона	S =	S =
5.	Радіус кола, описаного навколо трикутника	R =	R =
6.	Радіус кола, описаного навколо правильного трикутника	R =	R =
7.	Радіус кола, вписаного в  правильний трикутник	r =	+
8.	Радіус кола, вписаного в  квадрат	r =	r =
9.	Радіус кола, описаного навколо правильного шестикутника	R =	R =
10.	Радіус кола, вписаного в  правильний шестикутник	r =	r =
11.	Довжина сторони правильного шестикутника	a = R	+
12.	Довжина сторони квадрата	a = 4r	a = 2r

 

                      Додаток № 5.

Відповіді групи «Дослідники».

№ з/п	Назва формули	Формула	Правильна відповідь
1.	Теорема Піфагора
2.	Площа квадрата	S =	+
3.	Площа рівностороннього трикутника	S =	S =
4.	Формула Герона	S=	S=
5.	Довжина сторони правильного трикутника	a = 2r	+
6.	Радіус кола, описаного навколо правильного трикутника	R =	R =
7.	Радіус кола, вписаного в  правильний трикутник	r =	r =
8.	Радіус кола, вписаного в  квадрат	r =	+
9.	Радіус кола, описаного навколо правильного шестикутника	R =	R =
10.	Радіус кола, вписаного в  правильний шестикутник	r =	r =
11.	Довжина сторони правильного шестикутника	a =	a =
12.	Довжина сторони квадрата	a = R	a = R

                      Додаток № 6.

Відповіді групи «Практики».

№ з/п	Назва формули	Формула	Правильна відповідь
1.	Довжина сторони правильного трикутника	a = 4r	a = 2r
2.	Площа квадрата	S =	S =
3.	Площа рівностороннього трикутника	S =	+
4.	Формула Герона	S =	S =
5.	Довжина сторони квадрата	a = R	a = R
6.	Радіус кола, описаного навколо правильного трикутника	R =	R =
7.	Радіус кола, вписаного в  квадрат	r =	r =
8.	Радіус кола, вписаного в  правильний трикутник	r =	+
9.	Радіус кола, описаного навколо правильного шестикутника	R =	R =
10.	Радіус кола, вписаного в  правильний шестикутник	r =	r =
11.	Довжина сторони правильного шестикутника	a =	a =
12.	Довжина сторони квадрата	a = 2r	+