Урок + Презентація з геометрії для 8 класу на тему "Трапеція. Теорема Фалеса"

Урок геометрії, 8 клас

Тема. Урок узагальнення та систематизації знань, умінь та навичок з теми «Теорема Фалеса. Трапеція»

Грібінчак Любов Миколааївна, вчитель математики Желаннівського НВК Ясинуватського району

Мета: 

Навчальна:  повторити, систематизувати та узагальнити знання учнів з теми «Теорема Фалеса. Трапеція».

•  Учні повинні знати:

• означення, ознак та властивостей трапеції;
• теореми Фалеса;
• означення та властивостей кутів у колі;
• означення та властивостей чотирикутників, вписаних у коло, і описаних навколо кола.

• Учні повинні уміти  застосовувати вивчені твердження для розв’язання задач різного типу.

розвивальна: розвивати самостійність, уміння зосередитися, пізнавальний інтерес, логічне мислення, активність, культуру відповіді;

виховна: виховувати навички співпраці, почуття відповідальності, віру в свої можливості й здібності.

Тип уроку: узагальнення та систематизація знань.

Форма проведення: науково – практична конференція.

Наочність та обладнання: презентація, картки для учнів.

Підготовчий етап: тема, день і час проведення конференції оголошуються заздалегідь. Вчитель та учні розподіляють ролі, визначають учасників прес-конференції, які будуть відповідати на запитання. Решта учнів об’єднуються у групи, які виконують ролі кореспондентів.

Хід уроку

У класі розміщені вислови Фалеса: «Неосвіченість - важкий тягар" , «Пізнати себе важко, давати поради другим легко», «Блаженство тіла – в здоров’ї, блаженство розуму – в знаннях».

І.  Організаційний етап. 

Кабінет, де проводиться пресс - конференція, відповідно оформляється. За столом прес-центру си­дять учні, які виконують роль спеціалістів з даної теми. На слайді зображена хмара слів, з яких учні повинні відгадати  тему уроку. Вчитель пред­ставляє "спеціалістів".

ІІ.  Актуалізація опорних знань.

Вчитель.. Перед початком прес-конференції згадаємо основні поняття теми «Теорема Фалеса. Трапеція» за допомогою короткої розминки – тестових завдань на  Kahoot. com за адресою  https://create.kahoot.it/details/3d69d0c7-7109-4368-92d7-664c51dff45f .

ІІІ.  Мотивація навчальної діяльності.

Вчитель. Чотирикутники – найпоширеніші многокутники в нашому довкіллі. Стіни, стеля, підлога, двері, вікна, шибки, поверхня стола, грані бруска, дошки, цеглини, як правило мають чотирикутну форму.

У першому розділі ми ознайомилися з найважливішими властивостями чотирикутників, зокрема паралелограмів, прямокутників, ромбів, квадратів і трапецій, а також із властивостями чотирикутників, вписаних в коло і описаних навколо нього.

Сьогодні на уроці нам треба повторити і систематизувати знання з цієї теми перед контрольною роботою.

ІV. Узагальнення  й систематизація знань.

Вчитель. До нас завітали спеціалісти з питань  «Теорема Фалеса», «Коло та кути», «Коло та чотирикутники».

Отже, починаємо прес - конференцію.

Запитання. Кореспондент журналу «Історія математики».

Ми всі знаємо теорему Фалеса, у якій говориться, що паралельні прямі, що перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні. Цю теорему використовують при доведенні теореми про середню лінію трикутника, середню лінію трапеції та при діленні відрізка на рівні частини. Як бачимо теорема важлива. А хто такий Фалес?

Відповідь. Спеціаліст з питання «Теорема Фалеса» (відповідь з презентацією)

• ФАЛЕС ( 625 –  547 до н. е.), давньогрецький  філософ, родоначальник античної філософії та науки, засновник мілетської школи
• Ця  теорема названа на честь давньогрецького філософа, одного з семи великих мудреців давнини і «батька грецької геометрії» Фалеса Мілетського. За легендою, вона була сформульована в праці, яка не збереглась: у «Морській астрономії» Фалеса.
• Фалесу приписують відкриття та доведення теорем:

Кут, вписаний в півколо, прямий;

Вертикальні кути рівні;

В рівнобедреному трикутнику кути при основі рівні;

• Фалес також першим обчислив висоту однієї з єгипетських пірамід за її тінню. Відкрив  тривалість року і розділив його на 365 днів. Найбільш відомий вислів Фалеса: «Дотримуйся міри".
• Передбачив  сонячне затемнення.
• Фалес Мілетський мав титул одного з семи мудреців Греції, він був першим філософом, першим математиком, астрономом і, взагалі, першим по всім наукам в Греції. Він був тим же для Греції, що Ломоносов для Росії.

Запитання. Кореспондент газети «Математика у школі»

До нас надходять листи від школярів з запитаннями, які задачі найчастіше зустрічаються в завданнях ДПА та ЗНО з теми «Теорема Фалеса. Трапеція» та які теореми треба знати, щоб їх розв′язати. Дякую.

Відповідь. Спеціаліст з теми «Теорема Фалеса».

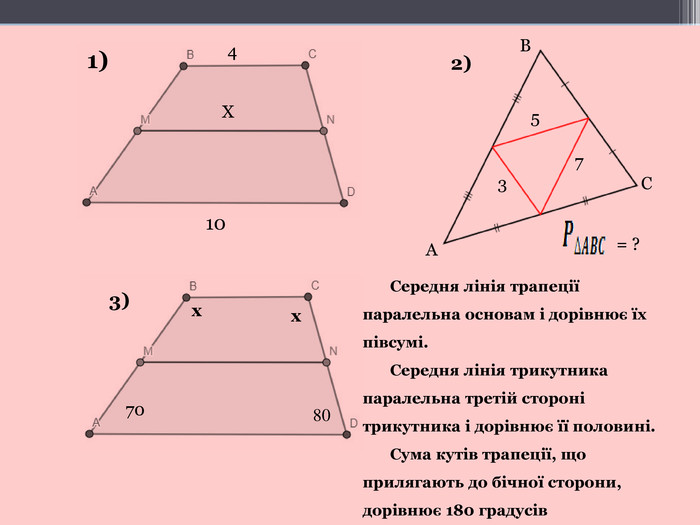
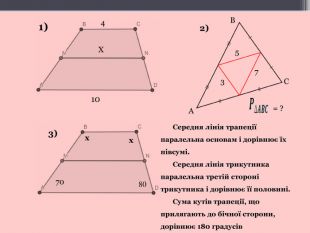
Серед найпоширеніших задач на дану теми є задачі на обчислення кутів трапеції;   обчислення сторін (периметра), висот, середньої лінії трапеції;    обчислення середньої  лінії трикутника. Для розв′язання цих задач використовуємо такі теореми «Сума кутів, прилеглих до однієї сторони трапеції, дорівнює », «Середня лінія трикутника паралельна третій стороні трикутника і дорівнює її половині», «Середня лінія трапеції паралельна основам і дорівнює півсумі її основ». Я пропоную розв’язати такі задачі. (малюнки на слайдах. А у учнів аркуші з малюнками і короткою умовою задач)

1. Кути трапеції дорівнюють 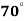і 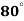. Знайдіть інші кути трапеції.(самостійно)
2. Знайдіть периметр трикутника, якщо його середні лінії дорівнюють 3 см, 5 см і 7 см.(усно)
3. Основи трапеції дорівнюють 4 см і 10 см. Знайдіть середню лінію трапеції.(усно)

Відповідь. Спеціаліст з теми «Коло та кути». 

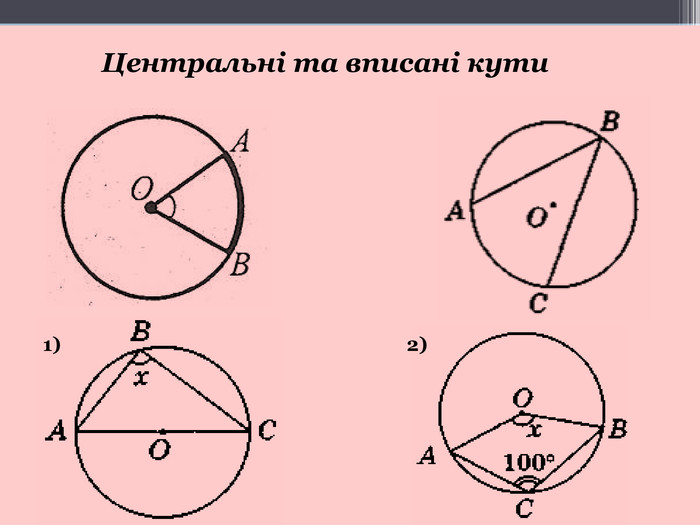
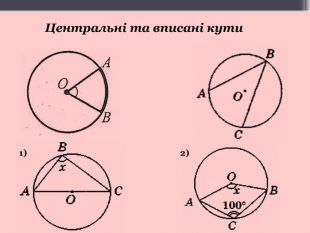
А я хочу доповнити відповідь попереднього доповідача. Учні часто роблять помилки у задачах, що стосуються центральних кутів та кутів, вписаних у коло.

 Для цього треба знати, що центральним кутом називають кут з вершиною у центрі кола. Вписаним у коло є кут, вершина якого лежить на колі. Центральний кут вимірюється дугою, на яку він спирається. Вписаний кут вимірюється половиною дуги, на яку він спирається.

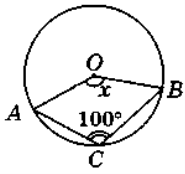
Я пропоную розв’язати такі задачі. (малюнки на слайдах. А у учнів аркуші з малюнками і короткою умовою задач) Задачу № 1 розв’язуємо усно

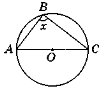1.                                     2)      

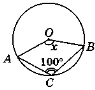
Задачу № 2 розв′язує клас спільно з  учнем, що працює  біля дошки

Запитання. Учень  10 класу.

До мене підійшла моя сестра, восьмикласниця. Одним із домашніх завдань з креслення було вписати у трапецію з основами 3см і 5 см, та бічними сторонами 4 см і 3 см, коло. У нас нічого не вийшло. Може поясните, чому?

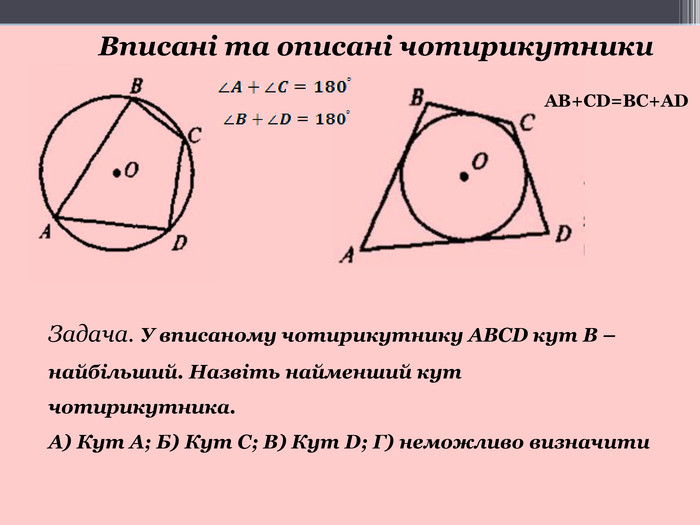
Відповідь. Спеціаліст з теми «Коло та чотирикутники».

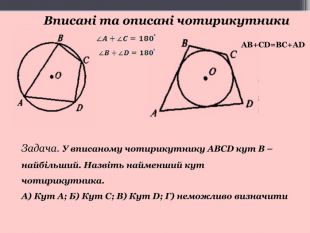
Типовим задачами є знаходження сторін та кутів вписаних і описаних чотирикутників. Для розв’язання задач використовують означення вписаного та описаного чотирикутника, теорему про те, що у вписаного чотирикутника сума протилежних кутів дорівнює , а у коло можна вписати такий чотирикутник, у якого сума протилежних кутів дорівнює

Наприклад, (усно)

1.  У вписаному чотирикутнику ABCD кут В — найбільший. Назвіть
найменший кут чотирикутника.

а) Кут А; б) кут С; в) кут D: г) визначити неможливо.

Якщо ж чотирикутник описаний, суми його протилежних сторін рівні. Справедлива і обернена теорема. У чотирикутник можна  вписати коло тоді,і тільки тоді, коли суми протилежних сторін, рівні.

Так чи можна вписати коло у дану трапецію? (Ні. Тому що суми протилежних сторін трапеції не рівні)

(Якшо є час, стор. 65, вар. 3 № 3)

V. Підсумок уроку

Вчитель. Наша конференція добігла кінця. Дякуємо всім учасникам. А зараз подумайте і дайте відповіді на запитання.

1. На уроці я робив …
2. Своєю роботою я задоволений / незадоволений тому що …
3. Цей урок здався мені …
4. За урок я б поставив собі, тому що …
5. Матеріал уроку я освоїв …
6. Мій настрій після заняття …

Домащнє завдання. Повт. стор.  68 -69, Задачі № 3 і №7 на стор. 67.(підручник

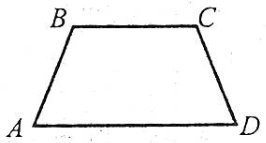
Дано: ABCD- трапеція,

A=,  D=

_______________________

Знайти: ,

Задача № 2.