Урок "Прогресії навколо нас"

Про матеріал

узагальнення та систематизація знань учнів про прогресії їх суми на прикладах задач із життя та історичних задач

Перегляд файлу

узагальнити та систематизувати знання учнів про прогресії; закріпити навички обчислення суми; показати практичне застосування теми на прикладах задач із життя та історичних задач; формувати навички роботи в групі; залучати дітей до знаходження і розв’язування проблем виробничого характеру, пов’язаних із застосуванням математики; виховувати інтерес до математики.

Учень повинен

знати:

• означення арифметичної і геометричної прогресій;

• яке число називають різницею арифметичної прогресії, знаменником геометричної прогресії;

• формули n-го члена арифметичної і геометричної прогресій, суми n - перших членів арифметичної і геометричної прогресій, суми спадної геометричної прогресії.

нормувати:

• знання і вміння знаходити n-й член арифметичної і геометричної прогресій;

• знання і вміння знаходити різницю арифметичної прогресії і знаменник геометричної прогресії;

• знання і вміння знаходити суму n перших членів арифметичної і геометричної прогресій; суму нескінченої спадної геометричної прогресії.

цінувати:

• уміння долати труднощі;

• прагнення досягти мети.

Урок - творчий звіт (узагальнення та систематизування матеріал).

Епіграф. Розв’язання простої, але не зовсім стандартної задачі може вимагати деякого напруження, зате натомість дає відчути тріумф відкриття. Д. Пойа.

Девіз уроку:

Приклади у навчанні корисніші за правила. Ісаак Ньютон

Обладнання. : мультимедійний проектор, презентації по темі

Очікувані результати:

Після уроку учні зможуть:

• застосовувати теоретичні відомості про прогресії до розв’язування вправ;

• навчитися сприяти свідомому застосуванню матеріалу під час розв’язування задач;

• звертатися до власного досвіду та залучати його до розв’язування вправ;

• набути навичок роботи в малих групах;

• набути навичок творчо мислити.

Хід уроку

I. Організаційний момент.

Вчитель:

Прогрес – це рух, це велич, це зростання,

Як Україні зараз він потрібний!

Прогресії – його сестриці рідній,

Щоб найскладніше розв’язать завдання.

І кожен з нас, як аксіому знає:

Без математики на ноги нам не стати,

Тож хай лунає лозунг наш крилатий

Прогресу без прогресій не буває!

ІІ. Мотивація навчальної діяльності.

Сьогодні на уроці ми підсумуємо вивчення одної з найцікавіших тем математики - прогресії. Їх внутрішня гармонія, строга витончена краса робить теорію арифметичної і геометричної прогресій відображенням фундаментальних властивостей об’єктивного світу, що існує незалежно від нас, нашої свідомості. На сьогоднішньому уроці ми будемо поглиблювати знання з цієї теми. Побачимо, як теорія, з якою ми ознайомилися на уроках математики, знаходить застосування в інших науках і життєвих ситуацій.

Девізом нашого уроку будуть слова видатного англійського математика і фізика Ісаака Ньютона: « Приклади у навчанні корисніші за правила».

- Перш ніж перейти до розв’язування вправ, давайте з’ясуємо, що ви чекаєте від уроку. (інтерактивна вправа «Мікрофон»)

- Щоб включитися до роботи, шановні учні, необхідні певні знання, які треба обов’язково перевірити. Для цього пограємо у гру «Дерево знань».

( Намальована яблуня з прикріпленими яблуками, на

звороті яких, написані запитання. Кожному учневі роздається дві картки – зелену і червону, якщо учень згоден з відповіддю гравця, він підіймає зелену,а якщо ні – червону; гравцям роздавати «яблука», якщо відповідь правильна; формули записуються на аркуші паперу. Кількість яблук – такий бал).

Означення геометричної прогресії.
Означення арифметичної прогресії.
Формула n-го члена арифметичної прогресії.
Формула n-го члена геометричної прогресії.
Сума n перших членів арифметичної прогресії.
Сума n перших членів геометричної прогресії.
Властивості членів геометричної прогресії.
Властивості членів арифметичної прогресії.
Як знайти знаменник геометричної прогресії?
За яких умов арифметична прогресія зростає, спадає, стала?
Як знайти різницю арифметичної прогресії?
Сума нескінченної геометричної прогресії.

Ми з’ясували, що ви маєте певні теоретичні знання. А зараз порахуємо усно.

І сурова, й солов’їна

Математики країна,

Праця тут іде завзята

Вмій лиш спритно рахувати.

2. Усна вправа «Знайди завдання».

(На екрані записано три стовпчики завдань. Учень називає стовпчик завдання і відповідь. Відгадане завдання викреслюється).

І. Знайдіть S₃, якщо: II. Знайдіть S₂₀₀, якщо:

b₁=-4, q=3 (-56); а₁=2,5, а₂₀₀=3,5 (600);

b₁=3, q=2 (21); a₁=5, a₂₀₀=200 (20500);

b₁=4, q=-2 (12); a₁=10, d=2 (41800).

III. Запишіть у вигляді звичайного дробу:

0,(59) (59/99);

0,(5) (5/9);

0, (12) (4/33).

-56; 600; 59/99; 12; 20500; 21; 5/9; 41800; 4/33.

-Ви добре впоралися з усним рахунком. Розв’яжемо ще ось таку задачу.

Задача – проблема.

Вам потрібно дійти до дверей, відстань до яких дорівнює 3м, але виконуючи такі умови: 1-ий крок - 1м, 2-ий крок - м, третій - м і так далі, кожний наступний крок у 2 рази менший від попереднього. Чи вдасться вам це зробити?

Хто вважає, що можна і не потрібно над цим сушити голову? (*)
Хто думає, що спочатку потрібно виконати деякі розрахунки? (**)

Вибираємо 2 учні від (*) групи, а (**) обчислюють.

Учень групи (*) відходить від дверей на 3м і починає міряти кроки, учні групи (**) – обчислюють.

Учитель: Розв’язуючи цю задачу, ви, мабуть, помітили, що вона виникла з потреб реального життя. Тому я хочу звернути вашу увагу на епіграф до нашого сьогоднішнього уроку. Розв’язання простої,але не зовсім стандартної задачі може вимагати деякого напруження, зате

натомість дає відчути тріумф відкриття. Д. Пойа

Отож, перейдемо до знайомства із задачами, які підготували учні – задачами на прогресії. Вони продемонструють вам, які предмети

потребують знань з теми «Числові послідовності», як можна використовувати інформацію про послідовності у життєвих ситуаціях.

Повернемося назад, в історію. А допоможе нам група «Істориків».

Виступ групи «Істориків»

НАЗАД, В ІСТОРІЮ!

Поняття числової послідовності виникло і розвивалося задовго до створення вчення про функції.

На зв’язок між прогресіями першим звернув увагу великий Архімед (близько 287–212 р. до н.е)

Стародавній Єгипет.

Відомості про прогресії вперше зустрічаються в документах Стародавньої Греції, які дійшли до нас. Уже у V ст. до н. е.

греки знали слідуючі прогресії і їх суми:

Прогресії у давнину.

Задачі на прогресії, які дійшли до нас із давнини, були зв’язані із потребами господарчої діяльності: розподіл продуктів, поділ спадщини і т.д. Так, наприклад:

Стародавній Єгипет.

Задача із єгипетського папірусу Ахмеса:

«Нехай тобі наказано: розділи 10 мір ячменю між 10 людьми, різниця ж між кожною людиною та його сусідом дорівнює міри».

Формула, якою в той час користувалися єгиптяни:

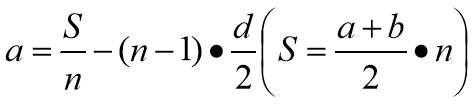Ще одним прикладом задач на прогресії є

задача із папірусу Райнда.

Задача из папируса Райнда.jpg

«У семи осіб по сім кішок; кожна кішка з’їдає по сім мишей, кожна миша з’їдає по сім колосків, із кожного колоска може вирости по сім мір ячменю. Наскільки великі числа цього ряду та їх сума?»

Більш за все нам сподобалася задача легенда про шахову гру, яку винайшли в Індії.

Задача – легенда.

Шахову гру винайшли в Індії. Ознайомившись з нею, індійський цар Сирам був захоплений її дотепністю і різноманітністю можливих у ній ситуацій. Коли він дізнався, що вона винайдена одним із його підданих, цар покликав до себе винахідника , для того щоб самому нагородити за успішний винахід. Винахідник Сета, з’явився до повелителя. Це був просто одягненний учений, який одержував засоби для життя від своїх учнів.

кар1 -Я хочу гідно нагородити тебе, Сета, за прекрасну гру, яку ти придумав, -сказав цар.

-Повелитель, - сказав Сета, - накажи видати мені за першу клітинку шахівниці одну

пшеничну зернину.

-Просте пшеничне зерно? – здивувався Сирам.

-Так, повелитель. За другу клітинку накажи видати 2 зернини, за третю - 4, за четверту - 8, за п’яту - 16, за шосту -32…

Роздратований Сирам пообіцяв Сету, що його слуги винесуть йому його мішок пшениці.

Коли на другий день придворні математики з’явилися до Сирама, то повідомили, що зерен не вистачить ні в яких коморах, навіть цілого царства. Не знайдеться такої кількості зерен і на всьому просторі Землі.

Зі здивуванням слухав принц Сета слова вчених.

Отже, скільки повинен цар видати пшеничного зерна Сету?

Розв’язання задачі – легенди.

yalma1 Дано: ; 1, 2, 4, 8, 16…

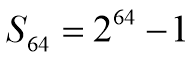
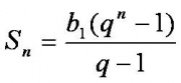n=64

Їх сума дорівнює

18 446 744 073 709 551 615.

Отже, нагородою за 64-и клітинки повинно бути

18 446 744 073 709 551 615

вісімнадцять квінтильонів

чотириста сорок шість квадрильонів

сімсот сорок чотири триліона

сімдесят три мільярди

сімсот дев’ять мільонів

п’ятсот п’ятдесят одна тисяча

шістсот п’ятнадцять зерен.

Якщо все це зерно помістити в комору висотою 4 метра і шириною 10 метрів, то довжина комори була б вдвічі більше, ніж відстань від Землі до Сонця...

Висновок: Якщо б царю вдалося засіяти пшеницею площу всієї поверхні Землі, враховуючи моря, і океани, і гори, і пустелі, і Арктику з Антарктикою, і одержати задовільний врожай, то, мабуть, років через 5 він зміг би розрахуватися.

Таку кількість зерен пшениці можливо

зібрати тільки з площі в 2000 разів большої від поверхні Землі. Це перевищує кількість пшениці, яка зібрана людством до цього часу.(сім раз відмір,а один – відріж).

Вчитель: Біологія це мудра наука,але теж не може обійтися без математики. І це зараз нам доведе група біологів.

Виступ групи «Біологів»

Наша група дізнавалася про те, як знання прогресії можуть допомогти під час вирішення деяких питань з біології.

До складу крові входять життєво необхідні $E:\відкритий урок картинки\Биология\eritrocit.jpg$ клітини – еритроцити, лейкоцити та тромбоцити, кількість яких впливає на самопочуття людини. Як це відбувається розглянемо на прикладі такої задачі (усно).

Задача № 1. Кількість еритроцитів

(з рахунком на 1 мм³) в крові людини становить на рівні моря – 5 млн. Через

кожні 600 м підняття вгору їх кількість збільшується на 1 млн. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест (4800 м). Чому це відбувається?

Застосовуємо наші знання з математики.

Розв’язання:

Ми маємо справу з арифметичною прогресією, перший член якої:

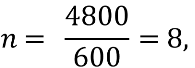
Висновок. У зв’язку з розрідженим повітрям в легені повинно більше потрапляти кисню, відповідно цьому збільшується кількість еритроцитів.

$E:\відкритий урок картинки\Биология\eritrocitngh.jpg$ 16

Процес розмноження відбувається прогресивно.

Пропонуємо розв’язати таку проблему.

Задача № 2 (письмово) .

Уявімо що на початку нашої ери жінка М народила дві доньки, кожна з них до 30 років народила теж 2 доньки і т.д. Чи можливо це? Скільки б за таких умов нащадків М жило б у нас час?

Розв’язання : Проаналізуємо цю задачу. В чому математична суть і яка математична модель цієї задачі?

Через кожні 30 років кількість жінок збільшується вдвічі. Тому маємо справу з геометричною прогресією у якої:

Використовуючи формулу суми, маємо:

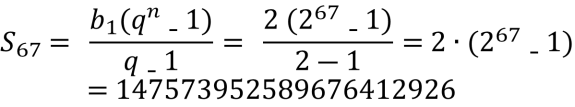
( знаходимо за таблицею).

Висновок: це число значно перевищує кількість людей на планеті. Тому це неможливо.

Вчитель:учасники ще однієї групи - фізики – презентують свій проект, який можна назвати «Кому потрібні гальма?».

Виступ групи «Фізиків».

$E:\відкритий урок картинки\дранік\ph19.jpeg$ Слів на описи не трачу

Словом не передаси

Безсловесно - дивовижної

Падіння вільної краси .

$E:\відкритий урок картинки\дранік\brjump2.JPG$ Так, бувають миті, що не повертаються двічі. Захоплено згадуєш хвилини вільного падіння. Не хочеться, щоб вони зникали.

Ось лечу, мені легко, я в захваті. В одну мить: я і простір.

Вільне падіння – це рух тіла під дією сили тяжіння без урахування тертя.

Кінцева швидкість при

вільному падінні: .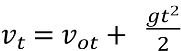

Прискорення вільного падіння: g=9,8 м/с²

Вашій увазі пропонуємо задачу. (Письмово).

Задача № 1. Тіло, яке вільно падає, проходить за першу секунду 4,9 м, а за $E:\відкритий урок картинки\дранік\004.jpg$ кожну наступну 9,8 м більше, ніж за попередню. Встановити, скільки секунд падає тіло з висотою

1960 м.

Розв’язання:

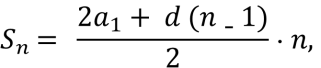
n=20 c.

Ну, а тепер про гальма. Ми кожного дня

чуємо «Обережно на дорозі!». Але не завжди правильно це розуміємо, забуваючи про наслідки.

Задача №2.

Гальмуючи, автомобіль за першу секунду проїхав 15м, а за кожну наступну – на 3 м менше, ніж за попередню. Знайти гальмівний шлях автомобіля.

Розв’язання.

а₁=15, d=-3, a_n=0.

a_n=а₁+ d(n-1), 15-3∙( n-1)=0, n=6.

S₆=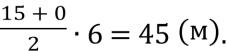

Висновок: ця задача застерігає кожного із нас, що треба бути уважним на дорозі.

Математику добре вивчаємо,

Самостійно проекти складаємо,

Однак зусиль ще треба локладати

Щоб досконало її знати.

Виступ групи «Практиків».

Готуючись до уроку, ми плідно попрацювали: знайшли і розв’язали багато прикладних задач. І нам хочеться поділитися

цим матеріалом. Тому нам прийшло на думку випустити збірник з цими задачами. Тому перед нами постали запитання:

Як можна повідомити мешканців нашого селища про наш збірник?
Як його прорекламувати?

Задача. Поширення чуток.

Я повідомлю нашу ідею о 12:00 год своїм трьом друзям, це займе , скажімо, 10 хв, тобто о 12:10 новина була відома лише чотирьом: мені і трьом моїм друзям. Довідавшись про цю новину, кожен з трьох розповів про неї трьом іншим. На це знадобилось теж 10 хв. Кожиний з дев’яти, які довідались про новину, поділився нею в найближчі 10 хв. із трьома іншими мешканцями селища. Якщо чутка поширюватиметься і надалі з такою самою швидкістю, то скільки пройде часу перш ніж усе селище

дізнається про неї?

Розв’язання.

Маємо геометричну прогресію 1, 3, 9, 27… .

Обчислимо, при яких n її сума стане більшою за 5200: S_n = 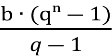; де b₁=1; q=3:1=3, маємо: 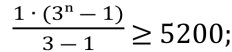3ⁿ≥5200∙2+

+1=10401; .

Пройде 8 десятихвилинок, тобто 1година і 20 хв, і о 13:20 новина буде відома всьому селищу.

Для того, щоб підвищити попит на наш збірник задач, необхідно його рекламувати, і дуже активно. Переговоривши з двома представника рекламних агенцій, я з’ясувала, що фірма «Шанс» на професійному рівні виготовить різноманітні рекламні проспекти нашої продукції за таких умов оплати: за першу партію 100 грн., а кожна наступна на 4% дешевша за попередню.

А представник фірми «Трейд-Лайн», запропонувавши такі послуги: виготовлення проспектів не тільки у чорному-білому, але й у кольоровому варіанті, при чому, виконають все дуже швидко, якісно, на любий смак. Але висунули такі умови оплати: перша партія коштує 100 грн., а кожна наступна має знижку 10%.

Учень. Розглянувши кожну умову, я хочу повідомимо вам про результати.

Фірма «Шанс»: перша партія 100 грн., а кожна наступна на 4 % дешевше попередньої, тобто: за першу збірку – 100 грн, за другу – 100-100∙0,04=96 грн., де 100∙0,04=4 грн., за третю – 96-4=92 і т.д.; це говорить нам про те, що маємо справу з арифметичною прогресією a₁ = 100, d = =-4;

Фірма «Трейд-Лайн»: за першу збірку - 100 грн., а кожна наступна збірка має знижку 10%, тобто: 100%-10%=90%, це 100∙0,9=90 грн., за третю - 90∙0,9=81грн. і т.д. : отже, маємо справу з геометричною прогресією

b₁= 100, q = 0,9 (100%-10%=90%=0.9)

Якщо нам треба розмістити замовлення на 5 збірників, то необхідно знайти S₅.

Фірма «Шанс»:

S_n∙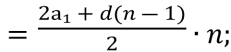

S₅ = 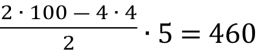(грн).

Фірма «Трейд-Лайн»

S_n = ;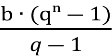

S₅=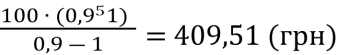

Висновок: Вигідніше розмістити замовлення, використавши послуги фірми «Трейд-Лайн».

Вчитель: ви дуже добре попрацювали, молодці! А зараз трішки розвантажемося.

V. Психологічне розвантаження.

У вас на партах лежать картки, на яких записані цифри від 1 до 9. Зараз зафарбуйте цей ряд двома різними кольорами у будь – якому порядку.

1, 3, 6, 7, 9; 2, 4, 5, 8.

А доки ви зафарбовуєте, я розповім вам про чудового математика на прізвище – Рамсей, який жив на початку ХХ століття. Він заснував теорію, яка стверджувала, що у світі немає абсолютного безладу. Навіть, здавалося б, саме неупорядкована система має визначені математичні закономірно всі. Згадайте, коли ви дивитесь на зірки, то може здаватися, що вони розміщені у хаотичному порядку. Але ще в давнину люди помітили там сузір’я Риб і Касіопеї, Лева і Оріона. І на ваших картках, здається , що цифри зафарбовані у випадковому порядку. Але Рамсей стверджував, що це не так, довівши

слідуючий факт: зверніть увагу, що хоча б 3 числа одного кольору складають арифметичну прогресію. Запишіть ці числа.

Vll. Рефлексія

Діти, а зараз оцініть самі свою роботу на уроці. Перед вами карточка із зображенням гори. Якщо ви вважаєте, що добре працювали на уроці і досягли бажаної мети, то намалюйте себе на вершині гори. Якщо залишилося щось незрозумілим, намалюйте себе нижче, а зліва чи справа вирішуйте самі,

та заповніть лист

самоконтролю:

VlІ. Підведення підсумків.

Давайте згадаємо початок нашого уроку,діти.

• Як ви вважаєте, епіграф відповідає сьогоднішньому нашому уроці?

Закінчіть речення:

Сьогодні на уроці я повторив…
Сьогодні на уроці я навчився…
Мені необхідно працювати над…
Найважчим для мене було…
Чому ми можемо вважати, що знання здобуті самостійно найбільш коштовні?

Вчитель: мені хочеться закінчити наш урок словами: «Не махай на все рукою, не лінуйся, а учись, бо чого навчився в школі, знадобиться ще колись!»

VІІІ. Домашнє завдання.

Кожному учневі знайти, або скласти та розв’язати дві задачі прикладного змісту, в яких застосовуються прогресії і подати їх до збірки, яка буде результатом вашої роботи.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Лисакова Ірина Миколаївна

Пов’язані теми

Алгебра, Розробки уроків

Додано

8 лютого 2021

Переглядів

658

Оцінка розробки

Відгуки відсутні