Урок "Рівняння кола" 9 клас

![]() Веселівський ліцей
Веселівський ліцей
Чмирівської сільської ради

Тема уроку. Рівняння кола.
Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв'язування задач.
Математична компетентність
Уміння: оперувати числовою інформацією, геометричними об’єктами на площині та в просторі; встановлювати відношення між реальними об’єктами навколишньої дійсності (природними, культурними, технічними тощо); розв’язувати задачі, зокрема практичного змісту; будувати і досліджувати найпростіші математичні моделі реальних об'єктів, процесів і явищ, використовувати математичні методи у життєвих ситуаціях.
Ставлення: усвідомлення значення математики для повноцінного життя в сучасному суспільстві, розвитку технологічного, економічного й оборонного потенціалу держави, успішного вивчення інших дисциплін.
Навчальні ресурси: розв'язування математичних задач, зокрема таких, що моделюють реальні життєві ситуації
Тип уроку: комбінований.
Наочність і обладнання: таблиця «Декартові координати і вектори на площині»
Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола.
Інтерпретувати та оцінювати результати; прогнозувати в контексті навчальних та практичних задач;
Хід уроку
I. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів під час їх виконання.
Залучити учнів-експертів до роз‘яснення домашнього завдання.
II. Аналіз результатів самостійної роботи
Синус, косинус, тангенс кутів від 0° до 180°.
Тотожності:
sin (180° – α) = sin α;
cos (180° – α) = – cos α.
Наводять приклади співвідношень, указаних у змісті;
пояснюють:
· що таке синус, косинус, тангенс кутів від 0° до 180°?
III. Сприйняття й усвідомлення нового матеріалу
Випереджальне завдання для учнів-експертів.
Розповідь одного з експертів, що опановували завдання дистанційно у формі лекції.
В алгебрі ми зустрічалися з різними рівняннями і будували їх графіки.
Рівнянням фігури на площині в декартових координатах називається рівняння з двома змінними х і у, яке задовольняють координати будь-якої точки фігури, і навпаки: будь-які два числа, які задовольняють це рівняння, є координатами деякої точки цієї фігури.
Яке ж рівняння має коло?
Для того щоб скласти рівняння кола, згадаємо його властивість, що міститься в означенні кола: усі точки кола розміщені в одній площині з його центром і однаково від нього віддалені.
Нехай центр кола М (а;b), а радіус кола R (рис. 1).
Позначимо на колі будь-яку точку А (х; у). Відстань від точки М до точки А дорівнює R, тобто AM = R, але за формулою відстані між двома точками маємо АМ2 = (х – а)2 + (y – b)2, або (x – a)2 + (y – b)2 = R2.(1)
Координати будь-якої точки цього кола задовольняють рівняння (1). Правильно і те, що будь-яка точка, координати якої задовольняють рівняння (1), належить колу.
Отже, (x – a)2 + (y – b)2 = R2 - рівняння кола. Якщо центр кола (рис. 2) лежить у початку координат, то воно має рівняння х2 + у2 = R2.
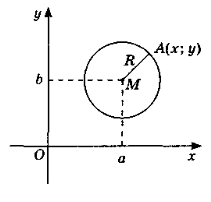
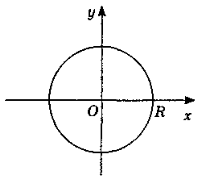
Рис.1 Рис.2
Розглянемо рівняння (1), у якому х і у — змінні координати точок кола, а числа а і b - відповідно абсциса і ордината центра, R - радіус кола. Отже, щоб записати рівняння кола, треба запам'ятати цю формулу і знати координати центра і радіус.
Наприклад, нехай M (-1; 2), a R = 2,тоді рівняння кола (x + 1)2 + (y – 2)2 = 4.
Виконання усних вправ
(Завдання записані на слайдах презентації та демонструються на моніторі комп‘ютера)
- Які з точок: А(1; 2), В(3; 4), С(−4; 3), D(0; 5), F(5; −1) - лежать на колі, рівняння якого х2 + у2 = 25?
- Запишіть рівняння кола радіуса 1, а координати центра:
а) (1;1); б) (-1; 1); в) (1;-1); г) (-1;-1)
- Укажіть координати центра і радіус кола, яке задане рівнянням:
a) (x– 1)2 + y2 = 9; б) (x + 1)2 + (у + 3)2= 1;
в) x2 + (y + 1)2 = 2; г) (x + 1)2 + (y + 2)2 = 7.
- Знайдіть на колі х2 + у2= 100 точки:
а) з абсцисою 6; б) з ординатою 8.
IV. Закріплення й усвідомлення нового матеріалу
Розв'язування задач письмово біля дошки
(Завдання задач записані на слайдах презентації та демонструються на моніторі комп‘ютера)
- Дано точки А(2; 1), В(−2; 5). Складіть рівняння кола, діаметром якого є відрізок АВ.
- Дано точки А(−1; −1) і С(−4; 3). Складіть рівняння кола:
а) з центром у точці А і яке проходить через точку С;
б) з центром у точці С і яке проходить через точку А.
- Знайдіть на осі Ох центр кола, яке проходить через точку А(1; 4) і має радіус 5.
- Складіть рівняння кола з центром (1; 2), яке дотикається до осі Ох.
- Складіть рівняння кола з центром (−3; −4), яке проходить через початок координат.
- Доведіть, що відрізок АВ, кінці якого А(2; −5) і В(5; −2) є хордою кола
(х − 5)2+(у + 5)2 = 9.
V. Домашнє завдання
Вивчити рівняння кола та розв'язати задачі.
- Коло задане рівнянням (х – 1)2+ (у + 3)2 =10. Чи проходить це коло через початок координат?
- Чи перетинає коло (х – 3)2+ (у + 5)2= 26 вісь Ох?Якщо перетинає, то знайдіть точки перетину з віссю Ох.
- Знайдіть рівняння кола, діаметром якого є відрізок АВ, якщо А(8; 5), В(2;−3).
-
 Виконати тестування в EasyQuizzy (тест 7) – додаткове завдання для учнів-експертів.
Виконати тестування в EasyQuizzy (тест 7) – додаткове завдання для учнів-експертів.
VI. Підбиття підсумків уроку
Завдання класу
- Запишіть рівняння кола.
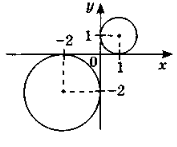
- Знайдіть координати центра і довжини радіусів кіл, зображених на рис. 3. Запишіть рівняння цих кіл. Рис.3
3. Укажіть рівняння кола, зображеного на рисунку.
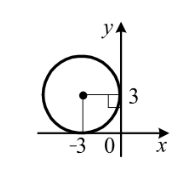 А)
А)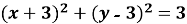
Б) 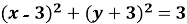
В)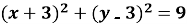
Г) 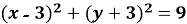
Комп’ютерне тестування
Порівняно з традиційними формами контролю комп’ютерне тестування має ряд переваг:
- швидке одержання результатів і звільнення викладача від трудомісткої роботи з обробки результатів тестування;
- індивідуалізація процесу навчання (автономність);
- певний психологічний комфорт учнів під час тестування;
- оперативність;
- підвищення об’єктивності оцінювання знань, і, як наслідок, позитивний стимулюючий вплив на пізнавальну діяльність учня;
- конфіденційність при анонімному тестуванні;
- тестування на комп’ютері більш цікаве у порівнянні з традиційними формами опитування, що створює позитивну мотивацію в учнів;
- виключення негативного впливу на результати тестування таких факторів як настрій, рівень кваліфікації й інші характеристики конкретного викладача;
- можливість застосування технічних засобів;
- універсальність, охоплення всіх стадій процесу навчання;
- контроль великого обсягу матеріалу;
- зменшення порівняно з традиційним опитуванням затрати часу на 50 %.
Використання різних конструкторів тестів потребує певних комп’ютерних знань з боку вчителя та час на його складання. Але затрачений час окупиться з лишком при неодноразовому використанні тестів. Те що комп’ютер дає можливість подавати запитання і варіанти відповідей у різному порядку забезпечує багатоваріантність тесту. Тобто аудиторію учнів, що тестуються можна значно збільшувати. При зміні програм учитель змінює, видаляє чи додає лише деякі завдання, що теж значно зберігає час.
- Вибір однієї правильної відповіді.
Зазвичай такі завдання в комп’ютерних конструкторах і web-конструкторах позначають маркером у вигляді кружечка, де правильна відповідь відмічається крапочкою. Це завдання типу «Виберіть правильне твердження» чи «Вкажіть неправильні твердження». Рекомендуються дескриптори (неправильна відповідь) підбирати так, щоб вони буди правдоподібні і обов’язково по тій темі, що і правильна відповідь, щоб зменшити ступінь відгадування. Тестологи рекомендують за допомогою цих завдань перевіряти знання теоретичного матеріалу.
- Множинний вибір правильної відповіді.
Завдання такого типу мають маркер у вигляді квадратика, відмічена відповідь позначається хрестиком” чи “галочкою”.
Також набувають популярності web-тести чи он-лайн тести. До попередніх перелічених переваг додається такий “плюс”, як збільшення аудиторії та можливість пройти тест у будь-який зручний час для учня, пройти його, як домашнє завдання чи додатково до уроків, навіть у кінці уроку, при умові вільного доступу до мережі Інтернет. Підтвердженням проходження тесту і отримання результату може бути “Сертифікат учасника”, який подається після збереження результатів проходження тестів.
1.1. Чому дорівнює сума 3,4 т + 700 кг.
А) 703,4 т Б) 4,1 т В) 410 кг Г) 1040 кг
1.2.Спростіть вираз ![]()
А) ![]() Б)
Б) ![]() В)
В)![]() Г)
Г)![]()
1.3 Яка з лінійних функцій є спадною?
А)![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
1.4. Який вираз є квадратом двочлена?
А)![]() Б)
Б) ![]()
В)![]() Г)
Г) ![]()
1.5. У кожному букеті має бути 2 червоні і 3 білі троянди. Яку найбільшу кількістъ таких букетів можна скласти з 40 червоних і 50 білих троянд?
A) 18 букетів Б) 17 букетів В)16 букетів Г) 15 букетів
1.6 Відомо, що c<d . Укажіть хибне твердження.
А) – 5с <− 5d Б) 5с < 5d В) с+5 <d+5 Г) с−5 < d−5
1.7 На одному з рисунків зображено графік функції ![]() . Укажіть цей рисунок.
. Укажіть цей рисунок.
![]()
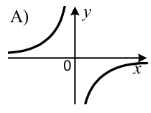
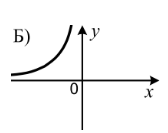
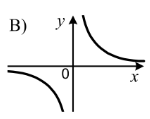
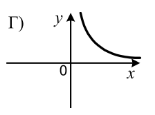
1.8 Деякий товар двічі подорожчав на 20%. На скільки відсотків збільшилась його ціна порівняно з початковою?
А) на 20% Б) на 24% В) на 40% Г) на 44%
1.9 Укажіть хибне твердження
А) суміжні кути мають спільну вершину
Б)суміжні кути мають спільну сторону
В)завжди один із суміжних кутів гострий, а інший - тупий
Г) якщо кути АОС і СОВ – суміжні, то промені ОА і ОВ - доповняльні
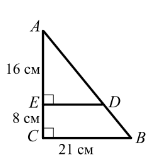 1.10 З точки D, яка належить гіпотенузі AB прямокутного трикутника ABC, зображеного на рисунку, опущено перпендикуляр DE на катет AC. Знайдіть довжину цього перпендикуляра.
1.10 З точки D, яка належить гіпотенузі AB прямокутного трикутника ABC, зображеного на рисунку, опущено перпендикуляр DE на катет AC. Знайдіть довжину цього перпендикуляра.
А) 10,5 см Б) 14 см В) 12 см Г) 16 см
1.11.Знайдіть сторону квадрата,діагональ якого дорівнює 4см.
А)![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.12. Укажіть рівняння кола,зображеного на рисунку.
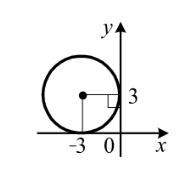 А)
А)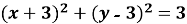
Б) 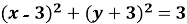
В)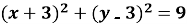
Г) 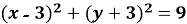


про публікацію авторської розробки
Додати розробку
