Скалярний добуток векторів
1
Тема уроку: Скалярний добуток векторів
Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв'язування задач; розвивати логічне мислення, просторову уяву, навички творчого мислення, увагу;виховувати математичну культуру учнів, сприяти вихованню інтересу до вивчення математики.
Тип уроку: засвоєння нових знань.
Обладнання: конспект уроку, кольорова крейда, підручник геометрія 9 клас, А.Г. Мерзляк, плакат «Вектори».
Хід уроку
І. Організаційний момент
(Заходжу до класу). Добрий день діти! Сідайте. (Перевіряю стан дошки, наявність вологої ганчірки, крейди, відмічаю відсутніх).
ІІ. Перевірка домашнього завдання
Хто не виконав домашнє завдання? Які виникли питання ?
Дуже добре, тоді якщо питань нема, то здаємо зошити.
ІІІ. Актуалізація опорних знань
Перш ніж почати нашу роботу давайте з вами пригадаємо попередній матеріал.
- Що таке вектор? Як позначаються вектори?
- Які вектори називаються однаково напрямленими (протилежно напрямленими)?
- Що таке абсолютна величина вектора?
- Що таке нульовий вектор?
- Які вектори називаються рівними? Яку властивість мають рівні вектори?
- Скільки різних векторів можна відкласти від заданої точки, які дорівнюють даному вектору?
ІV. Мотивація навчальної діяльності. Постановка завдань, мети уроку
На попередніх уроках ви навчились додавати та віднімати вектори, множити вектор на число.
Із курсу фізики ви знаєте, що коли під впливом постійної сили ![]() тіло перемістилося з точки А в точку В, то здійснилась механічна робота
тіло перемістилося з точки А в точку В, то здійснилась механічна робота ![]() .
.
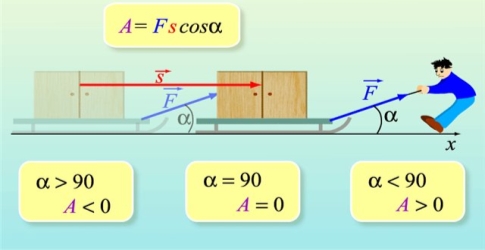
Цей факт показує, що для розв’язування таких задач, наших знань про вектор мало. Отже, сьогодні на уроці ми з вами розглянемо нове для вас поняття скалярний добуток векторів. З’ясуємо властивості скалярного добутку, навчимося знаходити кут між векторами. Розв’язувати задачі в яких використовується скалярний добуток векторів. Відкриваємо свої зошити і записуємо число, класна робота та тему нашого уроку: «Скалярний добуток векторів».
V. Вивчення нового матеріалу
Нехай ![]() - ненульові і неспівнапрямлені вектори. Від довільної точки О відкладемо вектори
- ненульові і неспівнапрямлені вектори. Від довільної точки О відкладемо вектори ![]() , відповідно рівні векторам
, відповідно рівні векторам ![]() .
.
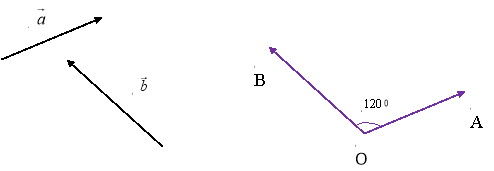
Величину ![]() називатимемо кутом між векторами
називатимемо кутом між векторами ![]() .
.
Кут між векторами позначається так: ![]() .
.
Якщо вектори ![]() співнапрямлені, то вважають, що
співнапрямлені, то вважають, що ![]() , якщо хоча б один із векторів нульовий, то вважають, що
, якщо хоча б один із векторів нульовий, то вважають, що ![]() .
.
Справедливо: ![]()
Означення. Скалярним добутком двох векторів називають добуток їх модулів і косинуса кута між ними.
![]()
Означення. Скалярним добутком двох векторів заданих їхніми координатами ![]() обчислюється за формулою:
обчислюється за формулою: ![]()
Наслідок: Косинус кута між ненульовим векторами ![]() та
та ![]() виражається формулою
виражається формулою 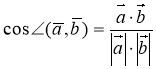 , яка випливає з означення скалярного добутку.
, яка випливає з означення скалярного добутку.
Косинус кута між ненульовими векторами із заданими координатами![]() обчислюється за формулою
обчислюється за формулою ![]()
Властивості скалярного добутку:
-
 ·
·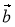 =
= 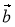 ·
·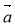 (переставний закон);
(переставний закон);
-
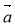 2 = |
2 = |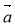 |2, або |
|2, або |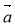 | =
| =  =
= 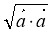 ;
;
-
(
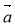 +
+ 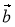 ) ·
) · 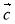 =
= 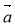 ·
·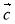 +
+ 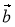 ·
·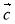 (розподільний закон);
(розподільний закон);
-
(λ
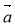 ) ·
) · 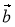 = λ(
= λ(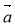 ·
·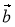 ) (сполучний закон);
) (сполучний закон);
- a ̅∙ 0 ̅=0.
Означення. Перпендикулярними називаються вектори кут між якими дорівнює 900. Пишуть ![]() .
.
Теорема. (Про скалярний добуток векторів)
Скалярний добуток двох ненульових векторів дорівнює нулю тоді й тільки тоді, коли ці вектори перпендикулярні.
Доведення:
-
Нехай:
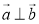 . Тоді
. Тоді 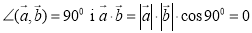 .
.
-
Нехай:
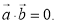 Тоді
Тоді 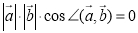 . Оскільки
. Оскільки 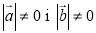 , то
, то 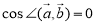 . Звідси
. Звідси 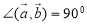 , тобто
, тобто  .
.
 Розв'язування задач
Розв'язування задач
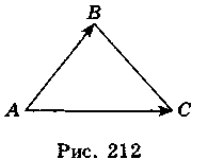
Сторона рівностороннього трикутника ABC дорівнює 13. Знайдіть скалярний добуток ![]() ·
·![]() (рис. 212).
(рис. 212).
Розв'язання
Оскільки |![]() |=|
|=|![]() |=13,
|=13, ![]() A=60°, то
A=60°, то ![]() ·
·![]() =
=
=|![]() |·|
|·|![]() |cos
|cos![]() A = = 13 · 13 cos60° = 169 ·
A = = 13 · 13 cos60° = 169 · ![]() = 84,5.
= 84,5.
Відповідь. 84,5.
VІ. Застосування знань
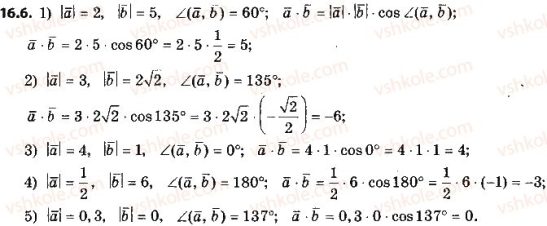
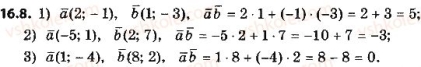
![]()
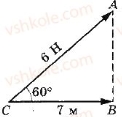

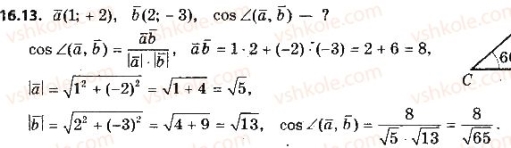
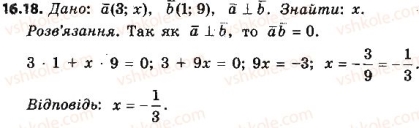
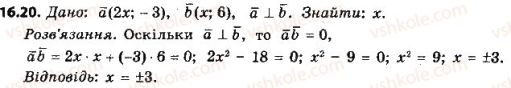

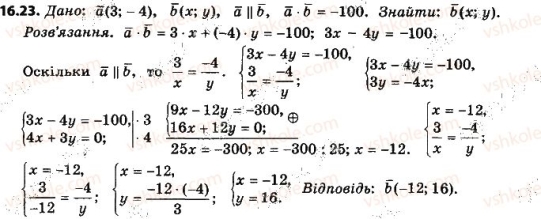
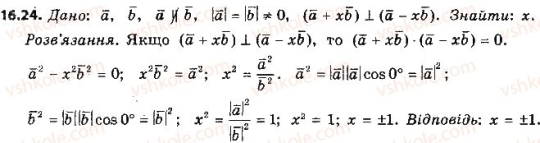
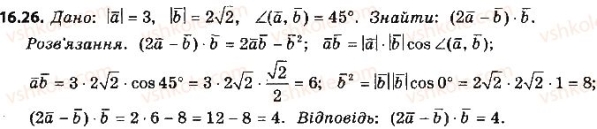

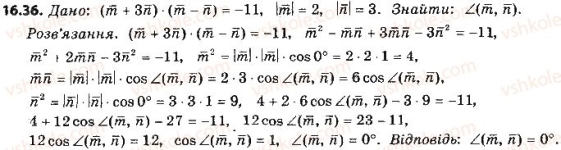
VІІ. Підбиття підсумків. Оцінювання учнів
Отже, ми з вами розглянули нову тему, а зараз дайте відповідь на наступні запитання.
Що ви дізналися нового? Що вам було незрозуміло? Що вам сподобалось?
VІІІ. Домашнє завдання
Опрацювати §4 п. 16. Розв’язати №16.7, 16.9,16.11.


про публікацію авторської розробки
Додати розробку
