Урок "Розв'язування задач на обчислення площ поверхонь циліндра і конуса"

Урок геометрії у 11 класі ( профільний рівень)

Тема уроку: розв’язування задач на обчислення площ поверхонь

                     циліндра і конуса

Мета уроку:1)  повторити формули для обчислення площі бічної та повної

                         поверхонь конуса та циліндра; формувати вміння й   навички                            

                         обчислювати  площі поверхні циліндра і конуса; вчити засто-

                       совувати вивчені формули при розв’язуванні задач практичного

                        спрямування;

                  2)  формувати уміння чітко, зрозуміло та лаконічно виражати свою

                         думку державною мовою, аргументовано доводити  правиль-

                         ність своїх суджень, міркувань та дій; формувати просторову

                         уяву.

Тип уроку: урок удосконалення знань і вмінь

Обладнання уроку: комп’ютер, заготовлені рисунки, підручник

                                    Хід уроку

І. Актуалізація опорних знань.

      1) Письмова фронтальна робота (на окремих аркушах)

За якою з поданих формул: 1)  πr² ;  2)  πrl;   3) 2πrh;  4) πr²+ πrl;  5) πrl+ 2πr²;

можна знайти :

а) площу бічної поверхні конуса;

б) площу основи циліндра;

в) площу повної поверхні циліндра;

г) площу основи циліндра;

д) площу повної поверхні конуса;

е) площу бічної поверхні циліндра.

    2) В конусі    r = 6 см,   h = 8 см . Знайти  S_б.п.

    3) В конусі    r = 6 см,   h = 8 см . Знайти площу осьового перерізу конуса.

    4)   В циліндрі   r = 6 см,   h = 8 см . Знайти  S_б.п.

    5)  В циліндрі   r = 6 см,   h = 8 см . Знайти  S_б.п.

   6) В конусі    r = 6 см,   h = 8 см . Знайти площу осьового перерізу конуса.

2) Усні задачі за готовими рисунками

ІІ.  Повідомлення теми і мети уроку

ІІІ. Формування вмінь і навичок

    1.Задача № 956 [ 1, ст.189] Скільки квадратних метрів жерсті піде на виготовлення водостічної труби завдовжки 5 м і діаметром 20 см, якщо на шви додають 10% площі поверхні труби.

Розв’язання.

h = 5 м,    d = 20 cм = 0,2 дм,   r = 0,1м    S_б.п.= 2πrh= 2·3,14·0,1·5 = 3,14 (м² )

Врахуємо, що на шви ще треба 10%:      3,14·1,1 = 3,454 3,5(м² )

2. Задача № 959 [ 1, ст.189] Діаметр циліндричного парового котла зав-довжки 3,8 м дорівнює 0,8 м. Знайдіть тиск пари на повну поверхню котла, якщо на 1 см²  пара давить із силою 10 Н.

Розв’язання.

S_п.п.= 2πrh + 2πr² = 2πr(r  + l) = 2·3,14·0,4· (3,8 + 0,8) = 11,6 (м² ) = 116000см²

р = 116000см² · 10Н = 1 160 000 Н·см²

3. Задача № 1002 [ 1, ст.198] Через дві твірні конуса, кут між якими α , проведено площину, що утворює з площиною основи кут β. Знайти висоту конуса, якщо площа перерізу S.

Розв’язання.

S_ABN = ;    S = ;   AN =; ;

З        ;     ;  

З ΔNOM:          ,     

ON = MN·sin= ==

4. Задача  № 1011(1) Знайти площу поверхні тіла, утвореного обертанням трикутника зі сторонами 7 см і 8 см та кутом 120⁰ навколо прямої, що містить найменшу сторону трикутника

Розв’язання.

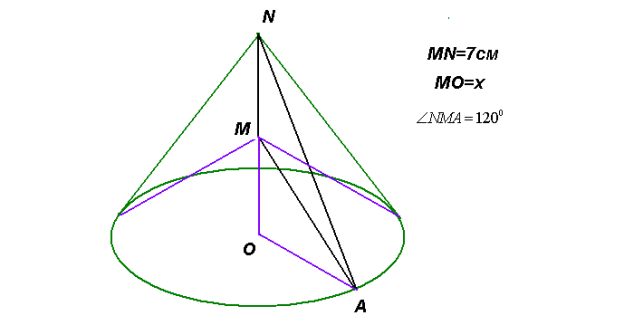
MN = 7 cм,     МА = 8 см,     ОМ = х,    NO = x + 7;

З  ΔNАM: АN² = MN² + MA² - 2 MN·MA·cos = 49 + 64 -2·7·8(- )= 169, AN = 13 cм.

З  ΔОАM:                 ОА² = 64 – х² ;

З  ΔОАN:                 ОА² = 169 – (x + 7)² ;     

169 – х² – 14х – 49 = 64 – х² ,    -14х = 64 + 49 – 169,         -14х = - 56,    х = 4  .

ОА² = 64 – 16 = 48;   ОА = 4см

S_п.п. = πrl + πrl₁ = πr (l+ l₁) = π· 4 · (8 + 13) = π· 4 ·21  = 84 π (см² )

ІУ.  Підсумки уроку.

У.  Домашні завдання : Повтор. п. 24-26. Виконати № 1010,  1012.[ 1, ст.199]

 Використані літературні джерела

1. Геометрія: 11кл.: підруч. для загальноосвіт.навч.закл.: академ. рівень, профіл. рівень /Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова, В.М. Владіміров.-К.: Генеза, 2011.- 336 с.