Урок "Розв’язування задач за допомогою пропорцій"

                                                                                                                                      Додаток

Урок 3.

"Розв’язування задач за допомогою пропорцій"

 

Мета уроку:

• повторити поняття прямої і зворотньої пропорційних залежностей;
• навчити виділяти в умовах задач дві величини і встановлювати вид залежності між ними;
• навчити робити короткий запис умови і складати пропорцію;
• розвивати здатність міркувати, ставити питання і відповідати на них;
• розвивати кругозір при вирішенні практичних завдань.

устаткування: картки зі словами «так» і «ні»; картки «Учитель-учень»; листи з друкованою основою; мультимедійний проектор; слайди з умовою завдань.

Хід уроку

1) Організаційний момент. Перевірка готовності до уроку. Повідомлення теми і мети.

Сьогодні ми навчимося вирішувати завдання за допомогою пропорцій. Ці знання вам знадобляться при рішенні задач з хімії, фізики, геометрії, географії, креслення і технології. Ви побачите великий зв'язок математики з іншими предметами.

2) Повторення.

1. Чи вірне висловлювання: (учні мають картки, на яких записані слова «так» і «ні» і відповідають за їх допомогою).

• Чим більше знаменник дробу, тим він більше.
• Чим ближче до 0 розташована точка на числовому промені, тим її координата менше.
• Зі збільшенням значення «х» значення виразу х² збільшується.
• Зі зменшенням значення «у» значення дробу  збільшується.
• Зростання людини прямо пропорційно її віку.
• Якщо одна з обернено пропорційних величин збільшується в кілька разів, то інша  зменшується у стільки ж разів.

2. Робота в парах. «Учитель-учень»

• Пара отримує дві картки. На одній завдання, а на іншій відповіді.
• Один учень відповідає на питання, інший, взявши картку з відповідями, виконує роль вчителя.

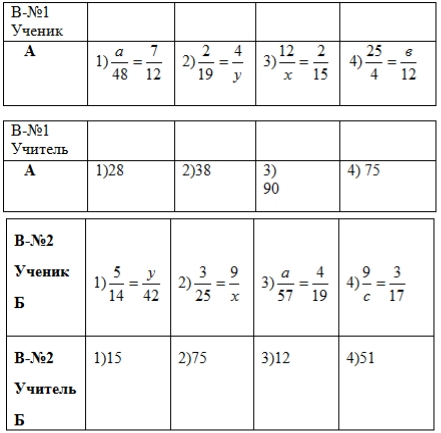
3. Питання.

• Які величини називають прямо пропорційними?
• Що можна сказати про відносини відповідних значень таких величин?
• Що можна сказати про відносини відповідних значень назад пропорційних достоїнств?

Ці властивості пропорційних величин використовуються при вирішенні завдань.

 

3) Пояснення нового матеріалу.

Задача№1. За 6 год потяг пройшов 480 км. Який шлях пройшов поїзд за перші 2 год, якщо його швидкість була постійною?

Розв’яжемо цю задачу новим способом.

1. Виділіть в умові задачі дві величини?
2. Яка між ними залежність?
3. У скільки разів зменшилась перша величина?

висновок: час і шлях зменшилися в одне і теж число раз, так як при сталій швидкості ці величини прямо пропорційні.

Для нового способу розв’язання буде потрібно короткий запис умови задачі:

Відповідь: 160 км.

Задача №2. Відстань між містами пасажирський поїзд пройшов зі швидкістю 80км / год за 3 год. За скільки годин товарний поїзд пройде на тій самій відстані зі швидкістю 40 км / год?

1. Назвіть дві величини?
2. Встановіть залежність між ними?
3. У скільки разів зменшилася перша величина?
4. Як зміниться друга величина?

У короткому  запису  умови завдання стрілки показують, що швидкість зменшилася, а час збільшився в одне і те ж число разів.

Швидкість руху (при постійному шляху) обернено пропорційно часу.

Відповідь: за 6 годин.

 

 

Розв’яжемо задачу другим способом

1) 80: 40 = 2 (рази) у стільки разів швидкість пасажирського поїзда більше,

2) 3 · 2 = 6 (ч) за стільки товарний поїзд проїде той же шлях.

Відповідь: за 6 годин.

Порівняти різні способи вирішення.

доповнення вчителя: Ще зустрінуться завдання, в яких «старий» спосіб не спрацює.

Узагальнення. Спосіб пропорцій полягає в наступному: (учні  пробують  під керівництвом вчителя скласти алгоритм).

1. Невідоме число позначається буквою х.
2. Умова записується у вигляді таблиці.
3. Встановлюється вид залежності між величинами.
4. Прямо пропорційна залежність позначається однаково спрямованими стрілками, а обернено пропорційна залежність - протилежно спрямованими стрілками.
5. Записується пропорція.
6. Знаходиться її невідомий член.

5) Рефлексія. Розв’язати  задачу з коментуванням.

Залежність між обсягом і масою прямо пропорційна.

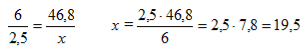
Відповідь: 19,5 г

Розв’язати задачу на дошці і в зошитах.

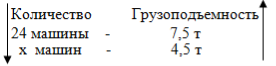
Залежність між кількістю машин і їх вантажопідйомністю обернено пропорційна.

х= 40

Відповідь: 40 машин.

 

Питання вчителя. Друзі, визначте в задачах залежність між величинами.

Завдання №3.За 2 год спіймали 12 карасів. Скільки карасів зловлять за 3 год?

завдання №4. Три півня розбудили 6 осіб. Скільки людей розбудять п'ять півнів?

Це завдання-жарти.

Завдання №5. Коли Вася прочитав 10 сторінок книги, то йому залишилося прочитати ще 90 сторінок. Скільки сторінок йому залишиться прочитати, коли він прочитає 30 сторінок?

У цьому завданні збільшення однієї і зменшення іншої величини відбувається не в одне й те ж число раз.

6) Тестова робота.

Учні отримують листи з друкованою основою.

Закінчити розв’язання задачі.

варіант №1

1) З 5 кг свіжих слив виходить 1,5 кг чорнослив. Скільки чорносливу вийде їх                      17,5 кг свіжих слив?

Закінчити розв’язування задачі.

Нехай вдруге вийде х кг чорносливу.

свіжі сливи		чорнослив
1 раз 5 кг	-	1,5 кг
2 раз 17,5 кг	-	х кг

Так як величини пропорційні, то можна скласти пропорцію:

відповідь:

2). На шлях від одного селища до іншого зі швидкістю 12,5 км/год велосипедист витратив 0,7 ч. З якою швидкістю він повинен був їхати, щоб подолати цей шлях за 0,5 год?

Закінчите розв’язання задачі.

Нехай х км/год - шукана швидкість велосипедиста. Швидкість руху (при постійному шляху) обернено пропорційна часу.

відповідь:

варіант №2

1) 3а 4 ч поїзд, не зупиняючись, пройшов 280 км. Скільки кілометрів він пройде з тією ж швидкістю за 6 год?

Закінчите рішення задачі.

Нехай вдруге поїзд пройде х км.

Так як величини пропорційні, то можна скласти пропорцію.

відповідь:

2) Щоб вивезти товар, який прибув на залізничну станцію, буде потрібно                                      21 автомашина вантажопідйомністю 2,5 т. Скільки необхідно  автомашин вантажопідйомністю 3,5 т?

Закінчите розв’язування задачи.

Нехай х машин потрібно вдруге. Кількість машин обернено пропорційно вантажопідйомності.

відповідь:

7) Підсумок уроку.

• Наведіть приклади прямо пропорційних величин.
• Наведіть приклади обернено пропорційних величин.
• Сформулюйте їх властивості.

 

8) Заповнити таблицю.

	Пряма пропорційність	Обернена пропорційність	Складання короткої умови	Складання пропорції за записом умови
Зрозумі(в/ла)
Не зрозумі(в/ла)
Частково зрозумі(в/ла)

 

9) Домашнє завдання.

Дякую за урок.