Урок. "Розвязування задач з теми 'Перпендикулярність прямої і площини'"

Конспект уроку з геометрії

на тему:

 Розв’язування задач з теми

«Перпендикулярність прямої і площини»

Тема. Розв'язування задач з теми «Перпендикулярність прямої і площини».

Мета:

• закріплення вмінь і навичок розв’язання задач на перпендикулярність прямих і площин у просторі;
• розвивати просторову уяву, логічне мислення;
• виховувати чесність, відповідальність, культуру математичних записів та мови.

Тип уроку: застовування знань, умінь і навичок

Обладнання. Мультимедійна презентація, підручник, креслярський набір

ХІД УРОКУ

I. Організаційний момент

Привітання. Перевірка присутності  учнів. Готовність учнів до уроку

ІІ. Перевірка домашнього завдання.

Наявність домашньої роботи у зошитах, перевірка правильності розв’язання шляхом усного коментування відповідей.

IIІ. Актуалізація опорних знань.

Математичний диктант

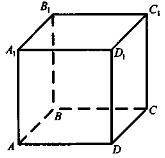
1. Дано зображення куба

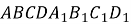
Користуючись зображенням, запишіть:

1)  площину, яка проходить через точку В прямої AВ і перпендику­лярна до неї; (2 бали)

2)  пряму, яка перпендикулярна до площини АВС і проходить через точку D; (2 бали)

3)  пряму, яка перпендикулярна до площини АВС і проходить через точку ; (2 бали

4)  площину, яка перпендикулярна до прямої BD; (2 бали)

5)  прямі, які перпендикулярні до площини АВС; (2 бали)

6)  площини, які перпендикулярні до прямої DC. (2 бали)

Відповіді. 1) (В); 2) D; 3) ; 4) (AВ); 5) D і ; 6) (AD) і (C).

III. Розв'язування задач.

Задачі розв'язуються біля дошки з коментуванням.

Задача 1. Побудувати переріз правильного тетраедра АВСD площиною, що перпендикулярна до ребра АВ і проходить через його середину. Знайти площу перерізу, якщо АВ = 12 см.     

Дано: АВСD — тетраедр, АВ = 12 см, МА = МВ.

Побудувати: а АВ.

Знайти:.

Розв'язання

У площині ∆ АВС через точку М проведемо СМ АВ. У площині ∆ АВD через точку М прове­демо DМ АВ.

∆ DМС є шуканим перерізом тетраедра АВСD .

∆ АВС = ∆ АBD, тому  СМ = DМ. Довжина відрізка СМ дорівнює АС∙см; СМ = 6 см.

Знайдемо площу ∆ DМС за формулою Герона: .

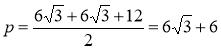(см).

(см²).

Відповідь.  см².

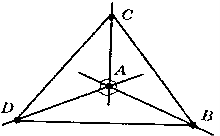                             Задача 2. Прямі AB, AC і AD попарно перпендикулярні. Знайдіть відрізок CD якщо: 1) AB =3 см, BC =7 см , AD = 1,5 см ; 2) BD = 9 см , BC= 16 см , AD = 5 см; 3) AB =a, BC =b, AD = c;

                  Дано: AB AC, ABAD, ACAD

                              AB =3 см, BC =7 см , AD = 1,5 см ;

                              BD = 9 см , BC= 16 см , AD = 5 см;

                                                                             AB =a, BC =b, AD = c.

                                                                Знайти: CD

                                    Розв'язання

За умовою    отже,   

 Прямокутні. Знайдемо довжину сторони DC.

1.   Розглянемо 

використаємо теорему Піфагора для прямокутного трикутника

Відповідь. 1) 6,5 см; 2) 15 см; 3)

Задача 3.  Доведіть, що через будь-яку точку А можна провести пряму, перпендикулярну до даної площини.

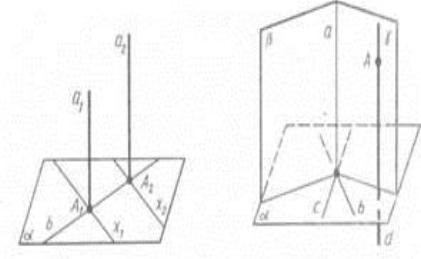
Доведення.

Проведемо у площині   дві прямі b і с, що перетинаються. Через точку їх перетину проведемо площини і , перпендикулярні до прямих b і с відповідно. Перетином їх буде пряма а. Пряма а перпендикулярна до прямих b і с, отже, і до площини  . Проведемо тепер через точку А пряму d, паралельну а. За теоремою 3 (Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої) вона перпендикулярна до площини

IV. Підсумок уроку.

Відповіді на запитання учнів

Оцінювання учнів

V. Домашнє завдання.

Зробити завдання  з розв’язком в зошиті за відповідним посиланням https://learningapps.org/view1464471