Урок-семінар "Теорема про три перпендикуляри"

10 клас

УРОК-СЕМІНАР

ТЕМА  ТЕОРЕМА ПРО ТРИ ПЕРПЕНДИКУЛЯРИ.

Мета уроку:

Дидактична  – Формування вмінь застосовувати теорему про три перпендикуляри до розв’язування задач.

Розвивальна –  розвивати пам'ять і мислення, просторову уяву;

Виховна – виховувати наполегливість і відповідальність, уважність,  любов до навчання та вміння працювати у колективі;

Формуємо компетентності: математичну, інформаційно-цифрову, соціальну, спілкування державною мовою.

Матеріально-технічне забезпечення та дидактичні засоби:

• презентація до уроку
• Інтерактивний комплекс
• програма Labwe Interactive Blackboard
• міні-зошит

ПЛАН СЕМІНАРУ

1. Теоретчна частина

• Гра "Заморочка із бочки" 
• Доведення теореми про три перпендикуляри

2. Задачі на обчислення – на самостійне опрацювання
3. Задачі на використання властивості точки, рівновіддаленої від сторін многокутника

ХІД УРОКУ:

1. Організаційна частина

2. Повідомлення теми і мети уроку:

Урок- семінар,

Перпендикуляр і похила. Теорема про три перпендикуляри

3. .Актуалізація опорних знань

Гра "Заморочка із бочки"  Перелік запитань:

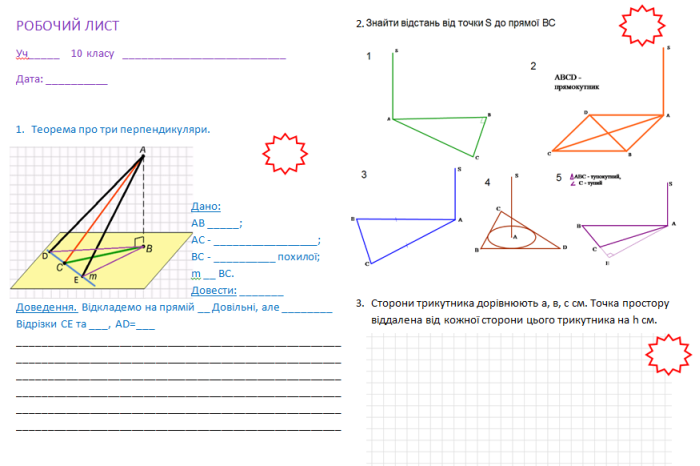
1. Теорема про три перпендикуляри

2. Записати формули радіусів вписаного та описаного кіл

3. Сформулювати властивості паралельного проектування

4. Означення та ознака перпендикулярності прямої та площини

5.

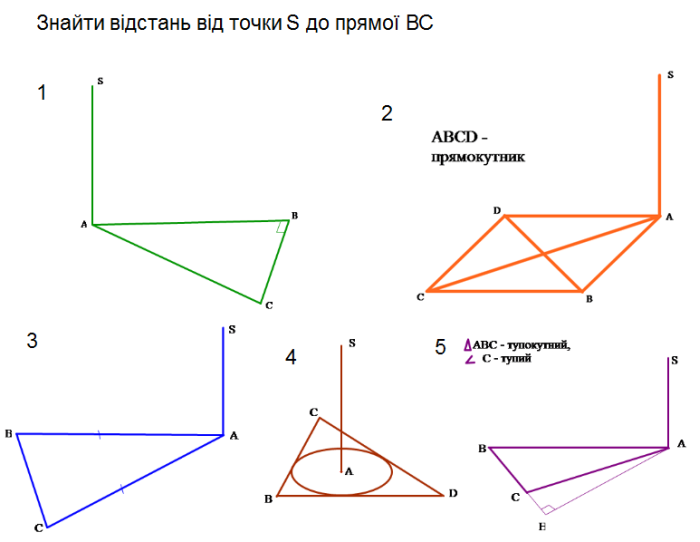
4. Розв'язування задач

1. Колективно

2. В парах

3. Угрупах

5. Самостійно

5. Підсумок  уроку,  рефлексія

6. Д/з  -  міні-зошит: № 7,8.

Додаток №1

Перпендикуляр і похила. Теорема про три перпендикуляри

Розв'язування задач.

1. Знайти довжину похилої, якщо довжина перпендикуляра дорівнює 4 см, а проекція похилої на площину - 3 см.
2. Знайти проекцію похилої на площину, якщо похила дорівнює 13 см, а перпендикуляр, проведений з тієї ж точки, -  12 см.
3. Знайти довжину перпендикуляра, якщо похила дорівнює 10 см, а проекція на площину - 8 см.
4. Скільки перпендикулярів можна опустити з даної точки до даної
   площини? Чому?
5. Скільки похилих можна провести з даної точки до даної площини? Чому?
6. Як слід установити на хрестовині ялинку, щоб вона була перпендикулярна до площини підлоги?
7. Як на практиці за допомогою виска перевірити вертикальність встановленого стовпа?
8. Знайти відстань від точки А до граней куба, якщо ребро куба дорівнює 10 см.

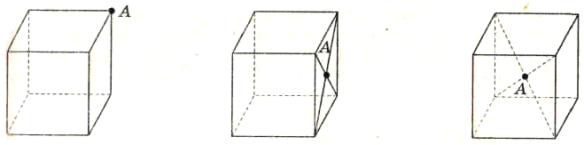
9. Із точки S проведено до площини 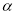   перпендикуляр SO та похилі SА і SВ. Довжини похилих відповідно дорівнюють 13 і 20 см. Довжина проекції похилої АS дорівнює 5 см. Знайти відстань від точки S до площини та довжину проекції похилої SВ.

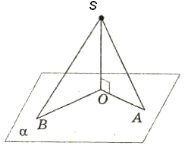
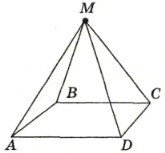
10. АВСD - квадрат, АВ = 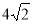см, МА = МВ = МС = MD =5 см. Знайдіть відстань від точки М до площини АВС.

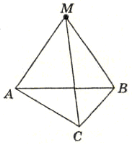
11. АВ = ВС = АС = 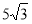см;   МА = МВ = МС = 13 см. Знайдіть відстань від точки М до площини АВС.

12. АВСD - квадрат, 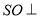(АВС), SО = 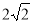см, АВ = 4 см. Знайдіть відстань від точки S до вершин квадрата.

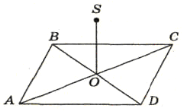
13. ∆АВС - правильний; точка О - центр трикутника; АВ = 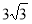см; 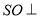(АВС);  SО = 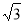см. Знайдіть відстань від точки S до вершин трикутника АВС.

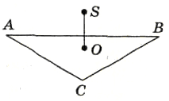
14. У рівнобедреному трикутнику кут при вершині дорівнює 120° , а бічні сторони - по 10 см. Поза площиною трикутника дано точку, яка віддалена від кожної із вершин на 26 см. Знайдіть відстань від цієї точки до площини трикутника. (Відповідь. 24 см.)
15. У трикутнику АВС 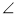А=45°, ВС = 12 см. Точка S знаходиться від його площини на відстані 6см і на однаковій відстані від кожної вершини трикутника. Знайдіть відстань від точки S до вершин трикутника. (Відповідь. 6 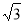  см.)
16. Трапеція вписана в коло, причому менша основа, яка дорівнює 16 см, стягує дугу 60°. На відстані 12 см від площини трапеції зна­ходиться точка, рівновіддалена від кожної її вершини. Знайдіть відстань від цієї точки до вершини трапеції. (Відповідь. 20 см.)
17. Через точку О перетину діагоналей квадрата АВСD проведено до його площини перпендикуляр МО дoвжиною 15 см. Знайдіть відстань від точки М до сторін квадрата, якщо його сторона дорівнює 16 см. (Відповідь. 17 см.)
18. Відрізок АS, що дорівнює 12 см, перпендикулярний до площини трикутника АВС, в якому АВ=АС=20  см,  ВС = 24 см. Знайдіть відстань від точки S до прямої ВС. (Відповідь. 20 см.)
19. До площини прямокутника АВСD, площа якого дорівнює 180 см, проведено перпендикуляр SD,  SD= 12  см,  ВС = 20 см. Знайдіть відстань від точки S до сторін прямокутника. (Відповідь. 12 см; 12 см; 15 см; 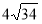см.)
20. Точка О — центр квадрата зі стороною 4 см, АО — пряма, що пер­пендикулярна до площини квадрата,  АО = 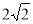    см. Знайдіть від­стань від точки А до сторін квадрата.
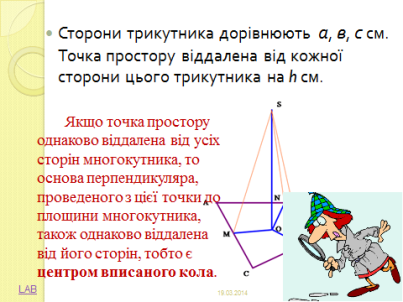
21. Точка S на 5 см віддалена від усіх сторін правильного трикутника, медіана якого дорівнює 9см. Знайдіть відстань від даної точки до сторін трикутника.
22. Точка S рівновіддалена від сторін правильного шестикутника, сторона якого дорівнює 6 см. Відстань від точки S до площини шестикутника дорівнює 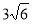  см. Знайдіть відстань від точки S до кожної сторони шестикутника. (Відповідь. 9 см.)
23. Точка S віддалена від кожної стороні ромба на 20 см, його діагоналі до­рівнюють 3О і 40 см. Знайдіть відстань від точки S до площини ромба.
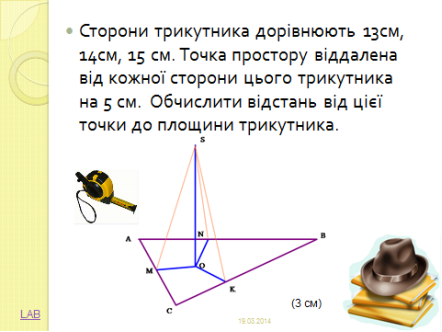
24. Бічна сторона рівнобедреного трикутника дорівнює 10 см, а основа 12 см. Точка S віддалена від кожної його сторони на 5 см.

Знай­діть: а) відстань від точки S до площини трикутника;

б) площу кру­га, вписаного в трикутник.

25. Прямокутна трапеція з гострим кутом в 45° і більшою бічною сторо­ною, яка дорівнює 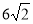см, розташована на площині 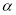. На відстані 4 см від площини 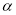знаходиться точка, рівновіддалена від кожної сторони трапеції. Знайдіть відстань від цієї точки до сторін трапеції.
26. Точка, однаково віддалена від всіх сторін рівнобічної трапеції, зна­ходиться на відстані 3 см від її площини. Периметр трапеції дорів­нює 48 см. Знайдіть відстань від точки до сторін трапеції.

Математичний диктант №1

МО - перпендикуляр до площини ОАВ; ОВ = 90°; МА і МВ — похилі.

Варіант   1 - МО = 1 см, ОА = 3 см, МВ = см;

Варіант   2 - МО = 1 см, ОВ = 4 см, МА =см.

Користуючись зображенням, знайдіть:

1. довжину невідомої похилої; (2 бали)
2. довжину невідомої проекції похилої; (2 бали)
3. довжину відрізка АВ; (2 бали)
4. відстань від точки О до середини відрізка АВ; (2 бали)
5. відстань від точки М до середини відрізка АВ; (2 бали)
6. відстань від точки А до площини МОВ. (2 бали)

Відповідь. 

Варіант   1. 1) см; 2) см; 3)  см; 4) см; 5) см; 6) 3 см.

Варіант   2. 1)   см; 2) 3 см; 3) 5 см; 4) 2,5 см;  5) см; 6) 3 см.

Математичний диктант №2

З центра правильного:

варіант   1 — трикутника;                         варіант   2 — чотирикутника

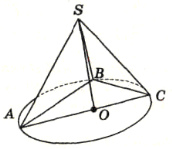
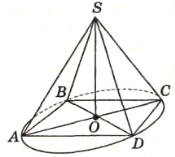
проведено перпендикуляр S0 до площини АВС, S0 = 1 см, АВ = 1 см.

Користуючись зображенням, знайдіть:

1. проекцію похилої SА на площину АВС; (2 бали)
2. відрізки, які дорівнюють відрізку ОА; (2 бали)
3. похилі, що дорівнюють похилій SА; (2 бали)
4. довжину похилої SА; (2 бали)
5. кут між похилою SА і перпендикуляром S0; (2 бали)
6. висоту трикутника SAB, проведену з вершини S. (2 бали)

Відповідь.  

Варіант   1. 1) см; 2) ОВ, ОС; 3) SВ, SС; 4) см; 5)  = 30° ; 6) см.

Варіант   2. 1) см; 2) ОВ, ОС, ОD; 3) SВ, SС, SD; 4) см; 5) , 6) см.

Математичний диктант №3

ABCD – прямокутник. .

Варіант 1 -  SA= см, АВ = 1 см, АD = 3 см;

Варіант 2  - SA= см, АВ = 1 см, АD = 2 см.

Користуючись зображенням, знайдіть:

1. довжину відрізка SВ; (2 бали)
2. довжину діагоналі АС; (2 бали)
3. довжину відрізка SD; (2 бали)
4. величину кута SВС; (2 бали)
5. величину кута SDС; (2 бали)
6. площу трикутника SDС. (2 бали)

Відповідь:

Варіант   1. 1) 2 см; 2) см; 3)  см; 4) см; 5) см; 6) .

Варіант   2. 1)   см; 2)   см; 3) см; 4) см;  5) см; 6) .

Математичний диктант №4

З центра правильного:

Варіант 1 – чотирикутника;                     Варіант 2 – трикутника

проведено перпендикуляр SO, SO=1см, АВ=1 см.

Користуючись зображенням, знайдіть:

1. відстань від точки О до точки А; (2 бали)
2. відстань від точки О до прямої АВ; (2 бали)
3. відстань від точки S до прямої АВ; (2 бали)
4. відстань від точки S до сторін даного многокутника; (2 бали)
5. відстань від точки S до вершин многокутника; (2 бали)
6. величину кута АSВ. (2 бали)

Відповідь.   Варіант   1. 1) см; 2) см; 3) см; 4) см; 5)  см ; 6) .

                    Варіант   2. 1) см; 2) ; 3) см ; 4) см; 5) см , 6) .