Урок: "Що таке функція?"
Цілі:
навчальна: домогтися усвідомлення учнями змісту понять „функція”, „функціональна залежність”, „область визначення функції”, „область значень функції”, способи задання функції; здійснити первинне закріплення змісту вивчених понять; розпочати роботу з вироблення вмінь обчислювати за формулою значення функції, якщо відомо значення аргументу, та розв’язувати обернену задачу;
розвивальна: формувати вміння самостійно здобувати знання, працювати з текстом підручника, розвивати розумову діяльність;
виховна: виховувати позитивне ставлення до знань
Тип уроку: формування компетентностей.
Обладнання: роздавальний матеріал, комп’ютер, таблиці.
Хід уроку
І. Організаційний момент.
ІІ. Мотивація навчальної діяльності.
Друзі! Якщо я запитаю, якого кольору мільйон або як звучить в музичному виконанні таблиця множення, то це вам видасться дивним. Насправді, в світі багато речей, що нас оточують, можна зв’язати між собою. Ще в давнину деякі вчені надавали особливе, інколи містичне, значення числам. Так, число 7 вважалось щасливим, а число 13 – „чортова дюжина” і з ним пов’язані різні неприємні обставини. Щоб зрозуміти зв’язок між різними величинами, потрібно познайомитися з поняттям „функція”.
Функція – одне з найважливіших понять математики, вона дає можливість досліджувати і моделювати не тільки стани, а й процеси. „Немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення” (К.Ф.Лебединцев)
Виявляється, що як і в повсякденному житті, так і в науці часто зустрічаються залежності між двома змінними, які можна виразити формулами або іншими способами. Тому на сьогоднішньому уроці ми нарешті з’ясуємо, як такі залежності визначаються в математиці, які математичні поняття пов’язані із цим поняттям, а також навчимося розв’язувати завдання на закріплення змісту розглянутих понять.
ІІІ. Актуалізація опорних знань.
У процесі вивчення та дослідження різноманітних явищ природи, розв’язування технічних задач тощо, доводиться розглядати не стільки змінні величини, взяті окремо, скільки зв’язок між ними, залежність однієї величини від іншої. Не існує змінних величин, які змінюються ізольовано, без зв’язку з іншими фізичними величинами. Наприклад...
Виконання усних вправ.
- Площа прямокутника зі сторонами 9 см та x см дорівнює S см2. Виразіть формулою залежність S від x. (Відповідь: S=9x)
- Потяг рухається зі швидкістю 70 км/год. За t годин він подолає S км. Задайте формулою залежність S від t. (Відповідь: S=70t)
- Нехай a см – довжина ребра куба, V см3 – його об’єм. Задайте формулою залежність V від a. (Відповідь: V=a3)
ІV. Вивчення нового матеріалу.
Прикладів залежностей між змінними можна навести чимало. Їх називають функціональними відповідностями, або функціями.
-
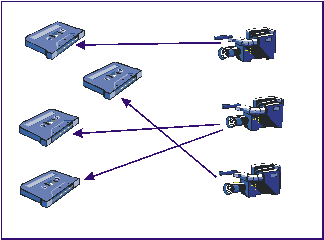
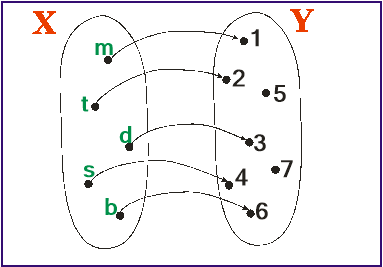 Уявіть собі, що перед вами не монітори комп’ютерів, а аеропорт, а це не калюжі, а множина X – пасажири, Y – місця в літаку. Нехай пасажири зайняли місця в літаку так: мама (m) займає крісло № 1, тато (t) – крісло № 2, донька (d) – № 3, син (s) – № 4, бабуся (b) – № 6. Неважливо, що частина крісел залишились незайняті. Головне те, що кожному пасажиру (кожному елементу xX) дісталося одне місце (поставлено у відповідність єдиний елемент yY).
Уявіть собі, що перед вами не монітори комп’ютерів, а аеропорт, а це не калюжі, а множина X – пасажири, Y – місця в літаку. Нехай пасажири зайняли місця в літаку так: мама (m) займає крісло № 1, тато (t) – крісло № 2, донька (d) – № 3, син (s) – № 4, бабуся (b) – № 6. Неважливо, що частина крісел залишились незайняті. Головне те, що кожному пасажиру (кожному елементу xX) дісталося одне місце (поставлено у відповідність єдиний елемент yY).
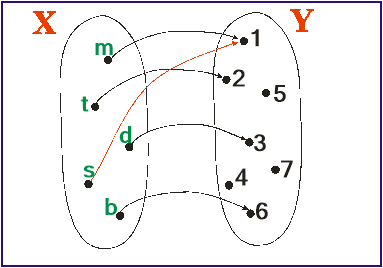
- Обставини змінились, і маму просять взяти сина на руки. Отримали іншу картину:
Все рівно, це функція, так як виконується умова: кожному елементу множини X поставлено у відповідність єдиний елемент із другої множини Y.
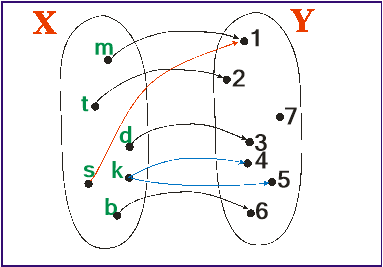
- В цьому літаку летить дуже „крутий” дядя, який хоче в одне крісло сісти, а на друге положити ноги. Така відповідність функцією не являється.
У розглянутих прикладах показано зв’язок між двома змінними. Одну з них, значення якої вибирають довільно, називають незалежною змінною, або аргументом. Другу змінну, яка залежить від аргументу, називають залежною змінною, або функцією. Незалежними змінними у наведених прикладах є: довжина сторони прямокутника, час руху потяга, довжина сторони куба, пасажири. Залежними змінними будуть: площа прямокутника, відстань, об’єм куба, місця літака.
Означення: Якщо кожному значенню змінної x з даної множини D відповідає єдине значення змінної y, то таку відповідність називають функцією. При цьому x називають незалежною змінною, або аргументом, y – залежною змінною, а множину D – областю визначення даної функції.
Якщо змінна y залежить від x, то використовують запис: y=f(x)
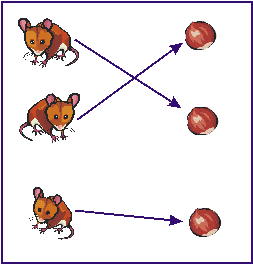
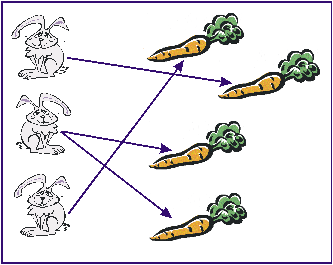 Приклади відповідностей
Приклади відповідностей
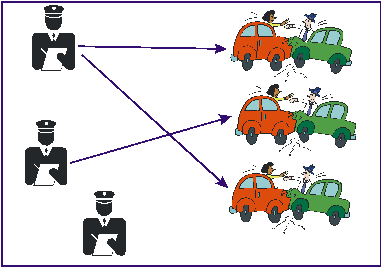
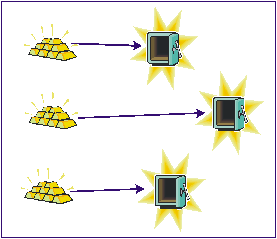
Тепер ви знаєте, що таке функція. Так ось, можна встановити відповідність між множиною натуральних чисел (скільки їх?) і спектром кольорів (скільки їх?). (Згадаємо, жартівливу приказку, яка допомагає запам’ятати кольори веселки: „Каждый охотник желает знать, где сидит фазан”). Отже, числу 1 можна поставити у відповідність червоний колір, 2 – жовтогарячий і т.д. по таблиці.
Таблиця1
Функціональна відповідність між числами, кольорами та нотами
|
Числа |
Колір |
Нота |
|
1 |
Червоний |
До |
|
2 |
Жовтогарячий |
Ре |
|
3 |
Жовтий |
Мі |
|
4 |
Зелений |
Фа |
|
5 |
Голубий |
Соль |
|
6 |
Синій |
Ля |
|
7 |
Фіолетовий |
Сі |
Починаючи з числа 8, все повторюється. А як же визначити, якого кольору число 29? Правильно, потрібно знайти остачу від ділення 29 на 7. Це буде 1. Отже, 29 – червоний колір і т.д.
Всі ви любите музику. Скільки всього нот? Хто перерахує їх? Так ось можна встановити функціональну відповідність між натуральними числами і нотами. Ви вже здогадалися, що числу 1 відповідає нота „до”, числу 2 – „ре” і т.д.
ІІ тепер ми не тільки можемо сказати, якого кольору мільйон (червоного, так як при діленні на 7 в остачі отримали 1), але і знаємо, що він „звучить” як нота „до”.
Склавши функціональну відповідність між натуральними числами і кольорами спектру та нотами (використовуємо таблицю 1), ми можемо визначити якого кольору ваш день народження і як він звучить.
Таблиця 2
Таблиця натуральних чисел
|
29 |
30 |
31 |
|
|
|
|
|
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
До |
Ре |
Мі |
Фа |
Соль |
Ля |
Сі |
Аналогічно ви можете розфарбувати і озвучити таблицю множення. Це ви виконаєте вдома, тим самим повторите табличку множення.
Таблиця 3
Таблиця множення
|
|
2 ре |
3 мі |
4 фа |
5 соль |
6 ля |
7 сі |
8 до |
9 ре |
|
2 ре |
4 фа |
6 ля |
8 до |
10 мі |
12 соль |
14 сі |
16 ре |
18 фа |
|
3 мі |
6 ля |
9 ре |
12 соль |
15 до |
18 фа |
21 сі |
24 мі |
27 ля |
|
4 фа |
8 до |
12 соль |
16 ре |
20 ля |
24 мі |
28 сі |
32 фа |
36 до |
|
5 соль |
10 мі |
15 до |
20 ля |
25 фа |
30 ре |
35 сі |
40 соль |
45 мі |
|
6 ля |
12 соль |
18 фа |
24 мі |
30 ре |
36 до |
42 сі |
48 ля |
54 соль |
|
7 сі |
14 сі |
21 сі |
28 сі |
35 сі |
42 сі |
49 сі |
56 сі |
63 сі |
|
8 до |
16 ре |
24 мі |
32 фа |
40 соль |
48 ля |
56 сі |
64 до |
72 ре |
|
9 ре |
18 фа |
27 ля |
36 до |
45 ре |
54 соль |
63 сі |
72 ре |
81 фа |
І так, ми з вами вияснили, що таке функція, незалежна змінна (аргумент), залежна змінна. А розглядаючи приклади функцій, ми не задумуючись розібрали способи задання функцій. Задати функцію – означає встановити правило (закон), за допомогою якого за даними значеннями незалежної змінної знаходять відповідні значення функції. Найчастіше використовують такі способи задання функції. Узагальнимо...
Способи задання функції
1) формула (S=9x; S=70t;V=a3) – найпоширеніший, основний спосіб в математичному аналізі;
2) опис („пасажири в літаку”);
3) таблиця (таблиця натуральних чисел, таблиця множення) – у техніці, природознавстві;
4) графік (більш детальніше зупинимось на наступним уроках) – у техніці та фізиці
А тепер перейдемо до більш серйозного етапу уроку – розглянемо поняття „область визначення”, „область значень” (пояснення проводжу по графіку деякої функції за програмою „Відкрита математика. Функції і графіки. Модель ”Властивості функції”). Складаємо опорний конспект.
Опорний конспект (виведений на моніторах комп’ютерів)
|
єдине О: функція – залежність x –––––––––––––––– y y=f(x) (відповідність)
x – аргумент y – значення функціїї D(f) – область визначення E(f) – область значень
1. Формула 3. Опис 4. Графік |
V. Розв’язування вправ.
- Вправи № 1, 2 виконуються „ланцюжком” біля дошки з коментуванням.
№ 1
Функцію задано формулою y=0,3x. Заповніть таблицю:
|
X |
–10 |
–3 |
–1 |
0 |
4 |
5 |
50 |
|
Y |
–3 |
–0,9 |
–0,3 |
0 |
1,2 |
1,5 |
15 |
4№ 2
Знайдіть область визначення функції, заданої формулою:
а) y=3x–7; б) ![]() ; в) y=5x2–x+3
; в) y=5x2–x+3
Відповідь: а) x – будь-яке число; б) x–5; в) x – будь-яке число
- Розв’язати самостійно вправи № 3, 4 і розшифрувати послання.

|
–1 |
30 |
7 |
–1 |
2005 |
19 |
5 |
№ 3
Функцію задано формулою y=2x+5. Знайдіть значення функції, коли x дорівнює: 1; 0; -3; 7; 1000.
Відповідь:
якщо x=1, то y=7 – Р; якщо x=–3, то y=–1 – Б ;
якщо x=0, то y=5 – І; якщо x=7, то y=19 – К;
якщо x=1000, то y=2005 – А
№ 4
Функцію задано формулою ![]() . При якому значенні аргументу значення функції дорівнює 20?
. При якому значенні аргументу значення функції дорівнює 20?
Відповідь: якщо y=20, то x=30 – У
Розв’язавши приклади, учені за допомогою вчителя вставляють букви у таблицю. Виходить слово „Бурбакі”.
VІ. Історична довідка.
Деякі приклади відповідностей між змінними, вченим були відомі дуже давно (у Вавилоні ще понад 3000 років тому складено таблиці квадратів і кубів натуральних чисел).Загальне поняття функції було введено тільки в XVІІ ст.. Спочатку Р.Декарт ввів поняття змінної величини і систему координат та залежність ординат точок графіка від їх абсцис. Слово „функція” (з латинського – дія, виконання) уперше ввів німецький математик Г.Лейбніц. Зусиллями багатьох математиків (Й.Бернуллі, Л.Ейлера, М.Лобачевського, Б.Больцано та ін.) поняття функції уточнювалося, розширювалося і наповнювалося новим змістом. Найзагальніше сучасне означення функції запропонувала в XX ст.. група математиків, яка виступала під псевдонімом Н.Бурбакі.
VІІ. Діагностика засвоєння знань і вмінь.
Математична естафета (на комп’ютерах – тестер „MyTestX”)
Учні з кожного ряду сідають по черзі до комп’ютера і розв’язують вправи. Перемагає команда, яка першою розв’яже всі приклади (враховується швидкість і якість – результати записані на комп’ютері)
Завдання тесту
Варіант І
- Площа прямокутника зі суміжними сторонами 5 см і x см дорівнює S см2. Виберіть формулу, яка задає функціональну залежність S від x.
А S=10+2x; Б S=5+x; В S=5x; Г S=25x2
- Дано функціональну залежність y=–23+0,7x. Вкажіть аргумент – незалежну змінну.
А y; Б x; В інша відповідь
-
Знайдіть значення функції
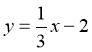 , якщо значення аргументу дорівнює –6.
, якщо значення аргументу дорівнює –6.
А –24; Б –12; В –4; Г 4
-
Задано функцію
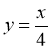 . Значення функції дорівнює –4. Знайдіть значення аргументу.
. Значення функції дорівнює –4. Знайдіть значення аргументу.
А –16; Б –1; В 1; Г 16
- Функція задана таблицею. Вкажіть функцію – залежну змінну
|
x |
1 |
2 |
3 |
|
Y |
4 |
9 |
16 |
А y; Б x; В інша відповідь
-
Укажіть значення змінної x, при яких функція
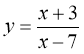 не має змісту.
не має змісту.
А –7; Б –3; В 3; Г 7.
Варіант ІІ
- Автомобіль рухався 6 год зі швидкістю v км/год пройшов шлях S км. Виберіть формулу, яка задає функціональну залежність S від v.
А S=6+v; Б S=6v; В ![]() ; Г
; Г ![]()
-
Дано функціональну залежність
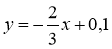 . Вкажіть аргумент – незалежну змінну.
. Вкажіть аргумент – незалежну змінну.
А y; Б x; В інша відповідь
- Знайдіть значення функції y=–0,2+0,8x, якщо значення аргументу дорівнює –1.
А –1; Б 0,28; В 0,6; Г 1
-
Задано функцію
 . Значення функції дорівнює –8. Знайдіть значення аргументу.
. Значення функції дорівнює –8. Знайдіть значення аргументу.
А –12; Б ![]() ; В
; В ![]() ; Г 12
; Г 12
- Функція задана таблицею. Вкажіть функцію – залежну змінну
|
x |
1 |
2 |
3 |
4 |
|
y |
3 |
6 |
9 |
12 |
А y; Б x; В інша відповідь
-
Укажіть значення змінної x, при яких функція
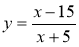 не має змісту.
не має змісту.
А –15; Б –5; В 5; Г 15.
Варіант ІІІ
- Автомобіль рухався t год зі швидкістю 65 км/год пройшов шлях S км. Виберіть формулу, яка задає функціональну залежність S від t.
А ![]() ; Б S=65+t; В S=65t; Г
; Б S=65+t; В S=65t; Г ![]()
- Дано функціональну залежність y=–0,5+3x. Вкажіть аргумент – незалежну змінну.
А y; Б x; В інша відповідь
-
Знайдіть значення функції
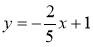 , якщо значення аргументу дорівнює 10.
, якщо значення аргументу дорівнює 10.
А –5; Б –3; В 3; Г 5
-
Задано функцію
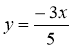 . Значення функції дорівнює –9. Знайдіть значення аргументу.
. Значення функції дорівнює –9. Знайдіть значення аргументу.
А –15; Б –5 ; В 5 ; Г 15
- Функція задана таблицею. Вкажіть функцію – залежну змінну
|
x |
12 |
9 |
6 |
3 |
|
y |
–4 |
–3 |
–2 |
–1 |
А y; Б x; В інша відповідь
-
Укажіть значення змінної x, при яких функція
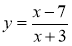 не має змісту.
не має змісту.
А –7; Б –3; В 3; Г 7.
Варіант ІV
- Кожну секунду в басейн надходить 0,5 м3. Скільки води стане в басейні через x с, якщо зараз у ньому 120 м3? Виберіть формулу, яка задає функціональну залежність об’єму V води в басейні від часу наповнення x.
А V=120–0,5x; Б V=120+0,5x; В ![]() Г
Г 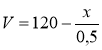
- Дано функціональну залежність y=0,2x–13. Вкажіть аргумент – незалежну змінну.
А y; Б x; В інша відповідь
- Знайдіть значення функції y=13–0,1x, якщо значення аргументу дорівнює –5.
А 8; Б 12,5; В 13,5; Г 18
-
Задано функцію
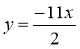 . Значення функції дорівнює 33. Знайдіть значення аргументу.
. Значення функції дорівнює 33. Знайдіть значення аргументу.
А –22; Б –6 ; В 6 ; Г 22
- Функція задана таблицею. Вкажіть функцію – залежну змінну
|
x |
1 |
2 |
3 |
4 |
|
y |
1 |
8 |
27 |
64 |
А y; Б x; В інша відповідь
-
Укажіть значення змінної x, при яких функція
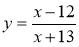 не має змісту.
не має змісту.
А –13; Б –12; В 12; Г 13.
VІІІ. Домашнє завдання. (виведене на моніторах комп’ютерів перед математичною естафетою)
§ 3 п.20, 21, пит.1–8 (ст..135), таблиця множення, № 791, 796, 804
ІX. Підсумок уроку.
Рефлексія
Учитель:
- Чи складною була тема? Що здалося найлегшим?
- В аркуші самооцінювання виставте собі оцінку за:
|
Листок само оцінювання Прізвище, ім’я______________________________________ а) розуміння навчального матеріалу (1–3 бали)___________; б) кількість і якість розв’язаних вправ (1–3 бали)_________; в) активність на уроці, висунення ідей, що привели до розв’язання поставлених завдань (1–3 бали)___________________________________; г) самостійність (1–3 бали)____________________________
|
Далі учитель, аналізуючи аркуші самооцінювання та, враховуючи відповіді учнів на уроці виставляє оцінки. Ряд, який працював найкраще, отримує додатковий бал.


про публікацію авторської розробки
Додати розробку


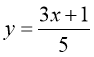 .
.
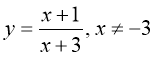 .
.
 2. Таблиця
2. Таблиця