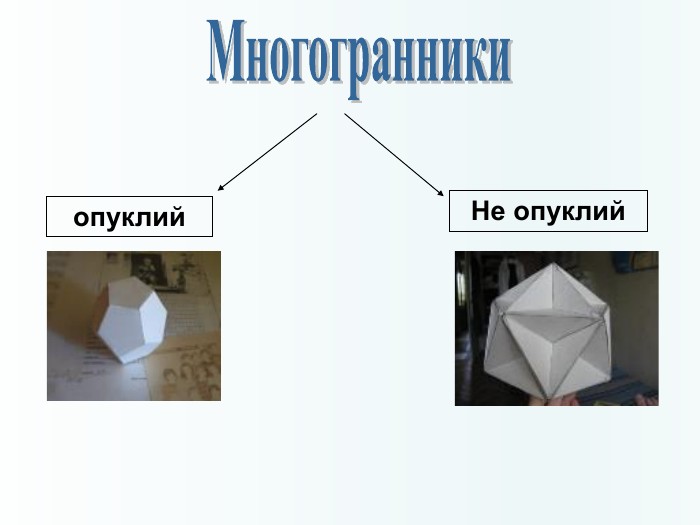
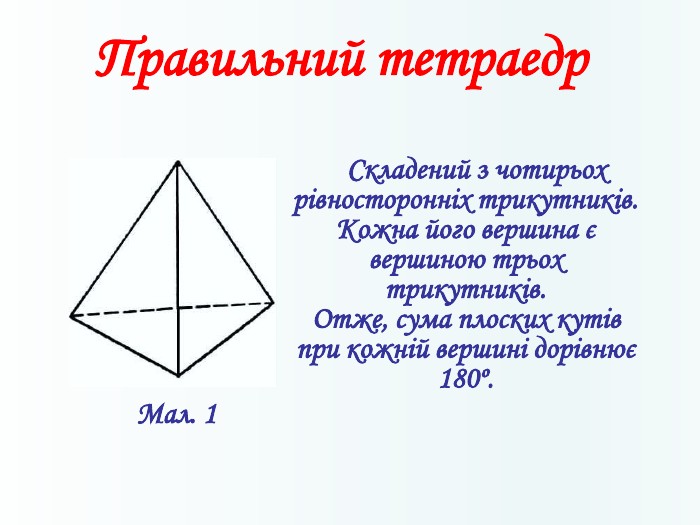
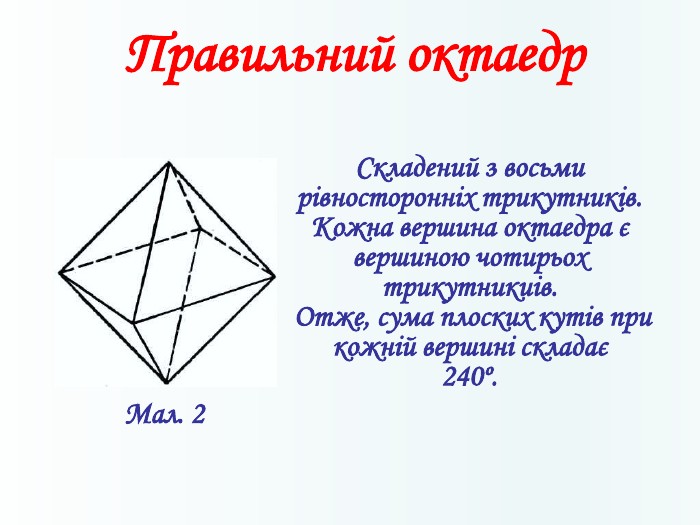
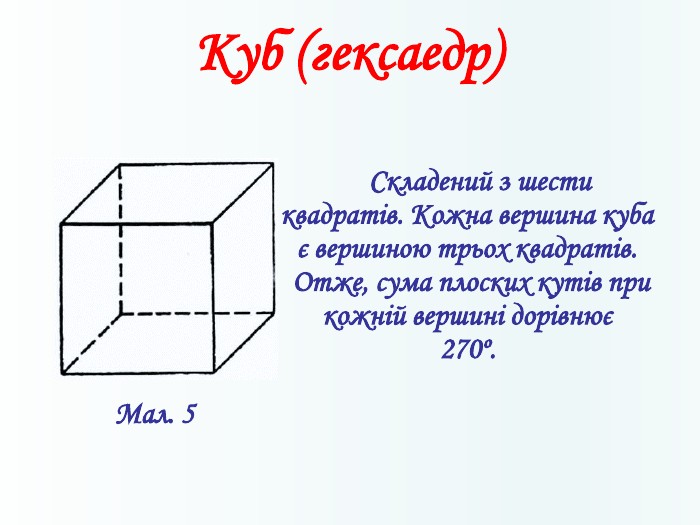
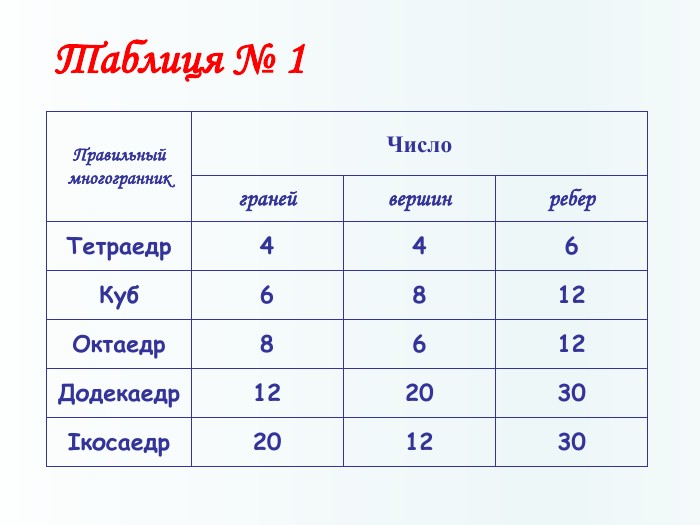
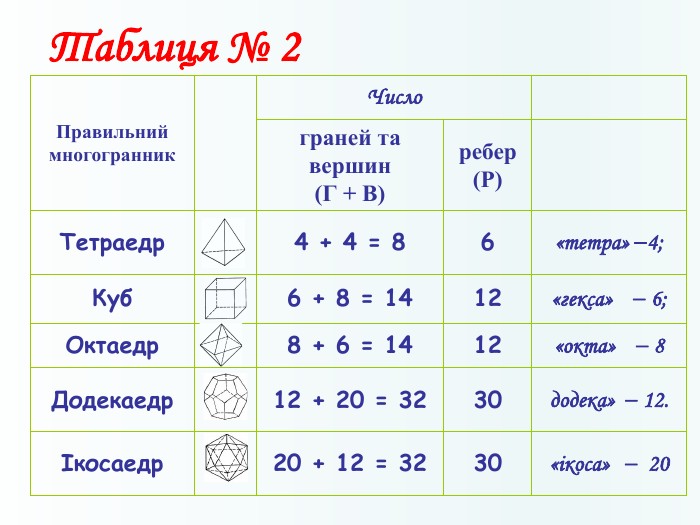
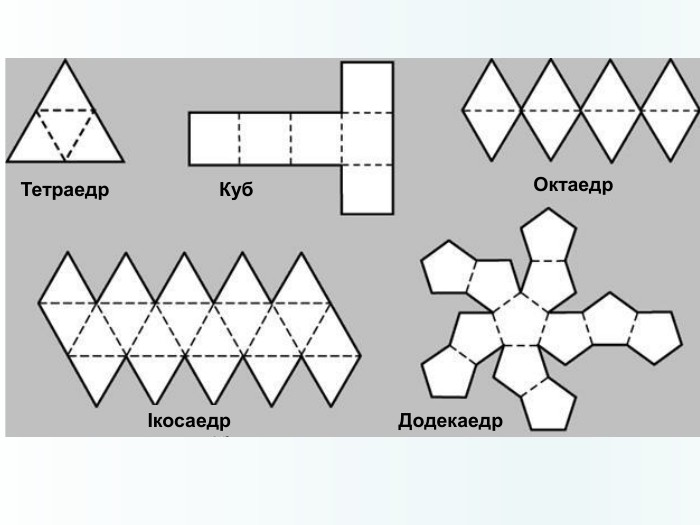
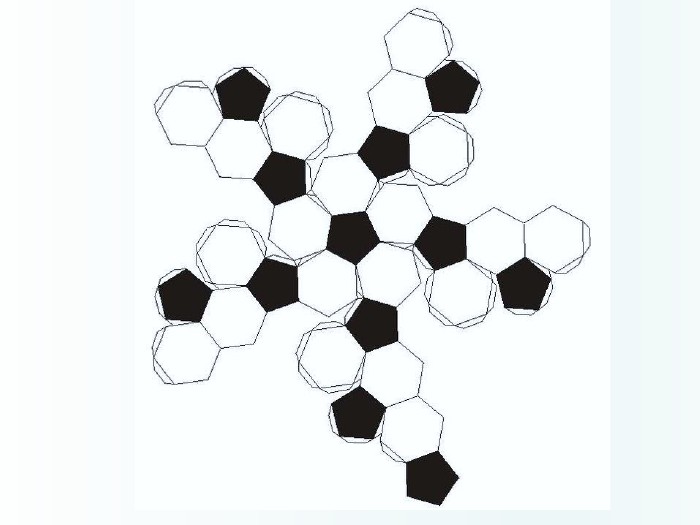
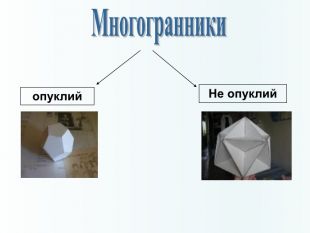
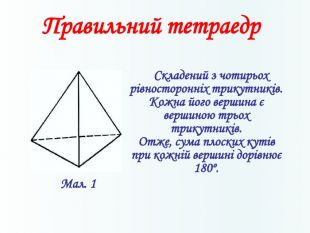
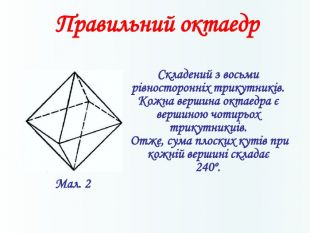
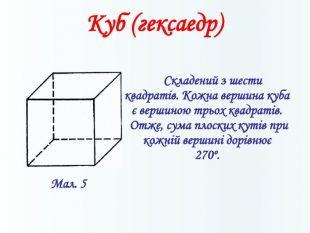
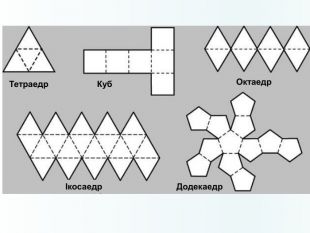
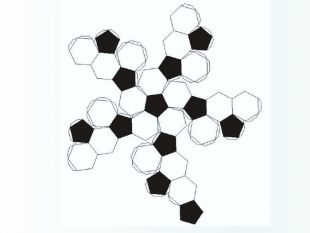
Многогранники, правильні многогранники
Про матеріал
Дана презентація призначена для ознайомлення учнів з типами многогранників та можливістю створити їх своїми руками. Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку