Урок "Співвідношення між тригонометричними функціями одного аргументу"

МЕТОДИЧНА РОЗРОБКА

УРОКУ З АЛГЕБРИ

на тему:

«Співвідношення між тригонометричними функціями одного аргументу»

Підготувала: Подляшаник Л.А.

Тема: Співвідношення між тригонометричними функціями одного аргументу.

Навчальна мета: Вивчення співвідношення між тригонометричними функціями одного аргументу. Формування умінь застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження значень тригонометричних функцій за однією відомою функцією.  

Виховна мета: виховувати вміння проводити об’єктивну самооцінку, самостійність та відповідальність.

Розвивальна мета: розвивати вміння самостійно міркувати, аналізувати та використовувати набуті знання на практиці.

Тип уроку: засвоєння нових знань.

Хід уроку І. Організаційна частина.

Організація робочих місць учителя і учнів, повідомлення теми, мети заняття. ІІ. Перевірка домашнього завдання. 1. Наявність виконаного письмового завдання перевіряють чергові.

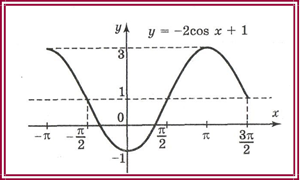
2. Розв’язування вправ:  1) Побудувати графіки функцій

•       y 2cosx 1;

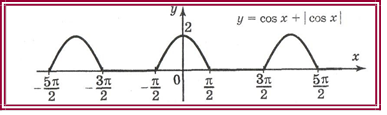
•       y  cosx  cosx ;

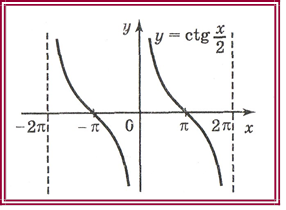
•       y  ctg ^x ;

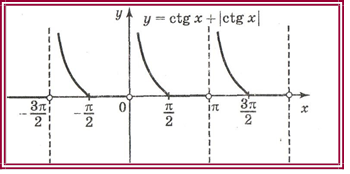
2  y  ctgx ctgx ;  y  tgx tgx .

Розв’язання:

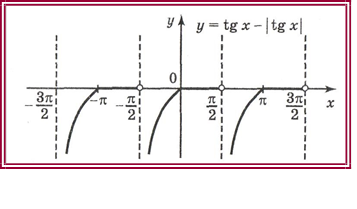
2) Знайдіть числове значення виразу.

tg²30^o 2sin60^o tg45^o tg60^o cos30^o 

•        3 ²   3          3          1          3          4          3          83 3

                     2          1 3                3 1 3                   

               ^ 3 ^_          2                    2      3                           2      3      2           6

_

2

•       sin0o 3cos sin2  030         2   2  1

                                            2            2                  2     4     2

•       2sin^ 2cos0^o tg^2  3 ¹ 21 3² 1,523  2,5

                            6                         3         2

ІІІ. Вивчення нового матеріалу а) Мотивація

Дуже часто при розв’язуванні задач виникає проблема: знайти значення тригонометричних функцій, якщо задано значення лише однієї з них. На сьогоднішньому занятті ми повинні пригадати формули (залежності), які пов’язують тригонометричні функції одного і того самого аргументу.

б) План вивчення теми

1.     Співвідношення між синусом і косинусом.

2.     Співвідношення між тангенсом і котангенсом.

3.     Співвідношення між тангенсом і косинусом, котангенсом і синусом.

в) Короткий конспект, тези нового матеріалу

Співвідношення між синусом і косинусом

Пояснення вчителя

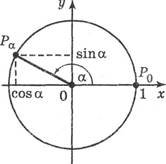
Нехай точка _x, y одиничного кола отримана поворотом точки Р₀ (1; 0) на кут  _ радіан. Тоді згідно з означенням синуса і косинуса маємо: x  cos,

 y  sin.

Оскільки точка  _x, y належить одиничному колу, то координати (х; у) задовольняють рівнянню  х² + у² = 1. Підставивши в це рівняння замість х і у значення cos_ і sin, отримаємо:

cos² sin² 1 Таким чином,

sin² cos²1

для всіх значень . Ця рівність називається основною тригонометричною тотожністю.

З основної тригонометричної тотожності можна виразити sin_ через cos_ і навпаки:

sin 1cos²;

cos 1sin².

Співвідношення між тангенсом і котангенсом.

 За означенням

sin tg         ;

cos cos^ ctg       .

sin

Почленно перемноживши ці рівності, одержимо: tgctg1.

Співвідношення між тангенсом і косинусом, котангенсом і синусом

Поділимо  обидві  частини основної тригонометричної тотожності  на  cos²_  (за умови,  що cos0), одержимо:

                                                                                               ²                      1     .

1tg  cos₂

Поділимо   обидві  частини основної тригонометричної тотожності  на  sin²_   (за  умови,   що sin0), одержимо:

                                                                                                ²                      1    .

1сtg  sin₂

IV. Закріплення вивченого:

Розв’язування вправ.

Усно. Чи існує число , яке одночасно задовольняє умовам:

1)    sin  , cos ;

2)    sin , cos ;

3)    sin 0,7, cos 0,3.

Розв’язання.

                                                                                       2                     2

1)    Оскільки sin²cos²^_^1_ ^_¹_^  ¹  ¹  ² 1, то не існує числа , яке

                                                                              3    3     9    9     9

одночасно задовольняло б даним умовам.

                                                                                         2                     2

2)    Оскільки sin²cos²^_^3_ ^_ ^4_  ⁹  ¹⁶ 1, то існує число , яке

                                                                                5     5     25    25

одночасно задовольняло б даним умовам.

3)    Оскільки sin²cos² 0,7² 0,3²  0,490,09 0,581, то не існує число , яке одночасно задовольняло б даним умовам.

Письмово. Спростіть вираз.

1)     1sin²cos²_;

2)     1cos1cos;

3)     sin⁴ 2sin²cos²cos⁴_.

Розв’язання.

1)      Подамо одиницю як суму sin²cos², тоді матимемо:

1sin²cos² sin²cos²sin²cos² 0.

2)      Скористаємося формулою abab a² b², подамо одиницю як суму sin²cos²1, матимемо:

1cos1cos1cos² sin²cos²cos² sin².

3)      Скориставшись формулою  a²  2abb²  (ab)² і врахувавши, що sin²cos²1, маємо: sin⁴ 2sin²cos²cos⁴ sin²_²  2sin²cos²cos²_

 cos² sin²_² 1² 1.

Усно. Чи існує число , яке одночасно задовольняє умовам:

1)     tg , сtg ;

2)     tg, сtg;

3)     tg 23, сtg 2 3.

Розв’язання.

1) Оскільки     tgctg  1, то існує число , яке одночасно задовольняє даним умовам.

2) Оскільки     tgctg  1, то існує число , яке одночасно задовольняє даним умовам.

3) Оскільки tgctg 2 ³2 ³ 2²  3²  43 1, то існує число _, яке одночасно задовольняє даним умовам.

Письмово. Спростіть вираз

ctg²sin²

1)      1sin₂

2)      cossin^2tg^

Розв’язання.

cos² 2 ctg2sin2 sin2cossin   _cos22_ 1



1         1sin2   2 cos 

sin

                      costg                       coscoscoscos

ctgcos

2         sin2      sin2 sin

                                        sin cos² 1                   cos² 1cos² sin²

                                 sin2 sin  sin sin             sin  sin  sin

Доведіть тотожність.

ctg  cos₂

ctgtg

Розв’язання.

                                        cos                cos

ctgctgtg  cossin   2 sincos2  cossinsin1cos  cos2

sin sin 



sin cos sincos V. Домашнє завдання.

Приклад 1. Спростити вираз.

1sin²

a)      tg_ cos

b)     1cos^_ sin^ _. sin 1cos

Розв’язання.

                  1sin²            cos² sin

a)      tg   sin_ cos cos cos

b)     1cos^_ sin^ _ 1cos² sin^2_

sin 1cos sin1cos

12coscos²sin² 12cos1                        21cos      2    .

                                                                                                  

                sin1cos        sin1cos sin1cos   sin

Приклад 2. Довести тотожність.

a)           sin12 cos12  tgctg2;

b)          sin⁴cos⁴12sin²cos²_ Розв’язання.

a)      Перетворимо праву частину рівності, враховуючи тотожності 

1tg² cos¹₂,

                                                                                                ²                      1     ,

1 ctg  sin₂ tgctg1.

tgctg² tg²2tgctgctg²tg²2ctg²  1ctg21tg2 sin12 cos12.

Одержали вираз, що стоїть у лівій частині рівності. Отже. Дана рівність є тотожністю.

b)     sin⁴2cos42 sin2 422sincos22cos212cossin42cos2sin2.2cos2 sin cos  2sin 

Підсумок уроку.

Вчитель відповідає на запитання учнів. Акцентує їхню увагу на основну тригонометричну тотожність.