Урок. "Способи подання і кодування інформації. Системи числення"

 

 

 

 

 

 

 

 

 

Відкритий урок з інформатики

на тему:

Способи подання і кодування інформації. Системи числення

 

 

 

 

 

 

 

 

Підготувала:

вчитель інформатики

Опорного ЗЗСО І-ІІІ ст. №1, м. Ходорів

Пелих Яромира Володимирівна

 

 

 

 

 

 

 

 

Тема: «Способи подання і кодування інформації. Системи числення.»

Обладнання та наочність: таблиці, слайди.

ХІД УРОКУ

I. Організаційний момент

II. Мотивація навчальної діяльності

Коли вам на уроці математики пропонують записати будь-яке число, ви, не за­мислюючись, зображуєте його за допомогою 10 арабських цифр. Ці цифри утворюють десят­кову систему числення, і саме в цій системі ви­кладається шкільна арифметика. Проте існують й інші системи числення. Про деякі з них ви ді­знаєтесь на сьогоднішньому уроці.

III. Вивчення нового матеріалу

Подання інформації в різних формах відбува­ється в процесі сприйнятті навколишнього світу живими організмами і людиною. Подання інфор­мації може здійснюватися за допомогою мовних засобів, які є знаковими системами.

Мова — система знаків і правил для відобра­ження, передачі, опису і зберігання даних. Осно­вою мови є алфавіт — впорядкована сукупність усіх знаків мови.

Кодування — процес перетворення символів одного алфавіту на символи іншого. Двійкові коди — спосіб подання інформації за допомогою двох символів — Oil (наприклад, число 34 ма­тиме вигляд 100010). Такий спосіб кодування обумовлений тим, що у пристроях комп'ютера використовуються елементи, які мають два різ­ні стани (що позначаються як 0 і 1). Це технічно легко реалізує зберігання й обробку інформації.

Біт (від англ. bit (абревіатура (b)inary dig(it)) — двійковий знак) — це найменша одиниця вимірю­вання інформації. Біт — це також одна комірка пам'яті, у яку можна записати 0 або 1.

Байт — це вісім послідовно записаних бітів:

Загальна кількість різних комбінацій двійко­вих значень у байті дорівнює 2⁸ = 256. Викорис­товуються також похідні одиниці вимірювання інформації: кілобайт (Кб), Мегабайт (Мб), гіга­байт (Гб).

1 Кб = 2¹⁰ = 1024 байтів;

1 Мб = 2¹⁰ = 1024 Кб;

1 Гб = 2¹⁰ - 1024 Мб.

  Матриця думок  

Класу пропонується розв’язати не складні, але неоднозначні задачі .

Задача1

Деяке плем’я має в алфавіті 24 букви і 8 цифр і більше ніяких знаків. Скільки мінімально розрядів їм необхідно для подання всіх символів?

(Відповідь: 24+8=32=2⁵ отже 5 розрядів)

Задача2

Лазерний принтер друкує зі швидкістю 5 сторінок за хвилину. Скільки знаків у секунду виводить принтер, якщо в середньому на одному листі 1,5 Кбайт інформації?

(Відповідь: 5*1,5*1024/60=128 знаків)

Щоб повідомлення можна було обробити за допомогою електронної апаратури (у тому числі, комп'ютера), його перетворюють в електричний сигнал. Сигнали бувають безперервними (анало­говими) або дискретними (імпульсними).

Відповідно до видів сигналів розрізняють два спосо­би надання інформації:

• Аналоговий — за допомогою безперервних сигналів. Прикладами аналогових способів передачі сигналу є людська мова, радіо, звукозапис на магнітні стрічки тощо.
• Цифровий — за допомо­гою дискретних сигна­лів. Найяскравішим прикладом дискретного способу подання інформації є обчислювальні процеси в комп'ютерах

  Мозковий штурм 

Класу пропонується загадка.

Було їй 1111 років.

Вона ходила на уроки

До 1001-го класу,

Носила 110 книжок щоразу.

Крокуючи десятком ніг,

Вона ходила вздовж доріг.

Рук, вух, очей по 10 мала,

І все, що поруч, помічала.

Коли виходила гуляти,

За нею бігло цуценятко.

І цей її 100-ногий друг

Мав один хвіст і 10 вух.

Все дуже дивним тут здається,

Нехай же відповідь дадуть:

У чому ж тут суть?

І хто секрет цей розгадає,

То скільки їй було років взнає!

Учні об'єднуються в 4 групи. Кожна група отримує завдання.

Перша група

Виписати й проаналізувати всі дані задачі.

Друга група

Виписати перші 15 натуральних чисел, у за­пису яких використовуються лише дві цифри — 1 і 0, і пронумерувати їх.

Третя група

10101 = 1 * 2⁴ + 0 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2° = 16+ 0 + 4 + 1 + 1 = 21.

1111 = 1* 2³ + 1 * 2² + 1 * 2¹ + 1 * 2° = ?           1001= ?         110 = ?

Через 7 хв кожна група записує на дошці ре­зультати своєї роботи.

Перша група  Роки – 1111. Клас – 1001. Руки – 10. Вуха – 10. Ноги – 10. Очі – 10. Голова – 1. Рот – 1. Ніс – 1. Кіски – 10. Портфель – 1. Лапи – 100. Хвіст –1.

Друга група

1	10	11	100	101	110	111	1000
1	2	3	4	5	6	7	8
1001	1010	1011	1100	1101	1110	1111
9	10	11	12	13	14	15

Третя група

1111 = 1* 2³ + 1 * 2² + 1 * 2¹ + 1 * 2° = 15                   

1001 = 1* 2³ + 0 * 2² + 0 * 2¹ + 1 * 2° = 9 

110 = 1 * 2² + 1 * 2¹ + 0 * 2° = 6

Відгадка в тому, що числа в ній подані у двійковій системі числення.

Система числення є позначенням чисел і при­йомами роботи з числами. Мінімальний набір знаків, за допомогою яких позначаються числа, називається алфавітом. Кількість знаків в алфа­віті називається основою системи числення.

  Повідомлення учнів  

Учень 1. У десятковій системі алфавіт утворений циф­рами 0, 1, 2, ..., 9, а основа дорівнює 10. З остан­ньою обставиною пов'язана назва самої системи.

Системи числення, незважаючи на свою простоту і природність, є результатом тривалої еволюції. Десяткова система виникла в резуль­таті лічби на пальцях. Зародилася вона в Індії у III столітті і була викладена в рукописах, які датуються IX століттям, арабською мовою. Тому цифри цієї системи називаються арабськими.

Учень 2. Давні шумери, які населяли Двуріччя в III тисячолітті до нашої ери, використовува­ли систему, алфавіт якої складався з шістдеся­ти цифр. За допомогою цієї системи можна було пронумерувати секунди у хвилинах, а хвили­ни — у годинах. Окрім ділення часу на години, шумери ввели ділення кутів на градуси, хвилини і секунди. Один кутовий градус містить 60 хви­лин: а одна хвилина — 60 секунд, тобто 1° (гра­дус) = 60' (хвилин) і Г = 60" (секунд). Система, побудована таким чином, називається шістде-сятковою.

Учень 3. У вавилонській системі числення перші п’ять чисел мали свої назви та записувались паличками у вигляді клинчиків. Числа більші за п’ять власних назв не мали. Число 10 називали «терміном» і позначали у вигляді широкого клина, що лежав. Для позначення всіх чисел використовували тільки два знаки: вузький клин, повернутий гострим кутом донизу, та широкий клин, повернутий ліворуч.

Двійкове числення не настільки давнє, як десяткове або шістдесяткове: воно було запро­поноване в 70-х роках XVII століття Готфрідом Лейбніцем. Алфавіт двійкової системи склада­ється всього з двох цифр – 0 і 1. В інформатиці, окрім двійкової системи, часто застосовується шістнадцяткова система числення (основа дорів­нює 16).

Учитель.  Система числення – це спосіб подання числа. Системи бувають позиційні, непозиційні, врівноважені, унарні, мішані.

Прикладом непозиційної системи числення є Римська система, в якій для запису цифр використовувалися букви: І=1; V=5; Х=10; L=50; С=100; D=500 і т.д. Наприклад 267 = ССLХVІІ.

Значення числа в позиційні системі з основою р визначається за формулою:

А _р= а_m*p^m+…+a₁*p¹+a₀*p⁰,  де m – номер розряду, р – основа, а – значення m-го розряду. За приклад візьмемо двійкову систему числення.

Двійкова система числення – це система, в якій для запису чисел використовують дві цифри – 0 I 1. Основою двійкової сис­теми числення є число 2.

Окрім двійкової системи числення існують інші нетрадиційні системи – 5, 7, 8,… та ще одна досить цікава – 16. Цікава тим, що  її алфавіт складається не лише з цифр, ай букв, тобто 0, 1, 2, …, 9, А=10, В=11, С=12, …, F=15.

Наприклад, число в 16-ій системі матиме вигляд (3АС)₁₆, а його значення в 10-ій системі буде таким: (3АС)₁₆ = 3*16² + 10*16¹ + 12*16⁰ = (940)₁₀

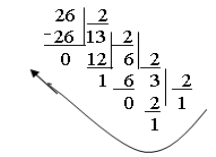Для переведення числа з однієї системи числення в іншу для р>q потрібно послідовно ділити його на q, тобто на основу тої системи числення, в яку переводимо число, поки не отримаємо остачу меншу за q. Число  в новій системі запишеться у вигляді остач від ділення, починаючи з молодшого розряду результата. Наприклад:

 

 

 

 

 

 

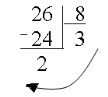
  (26)₁₀ = (32)₈                  (26)₁₀ = (11010)₂

Правило виконання операції додавання є од­наковим для всіх систем числення: якщо сума цифр, які додають, більша або дорівнює осно­ві системи числення, відбувається перенесення одиниці в наступний ліворуч розряд. Правила додавання у двійковій системі такі:

Додавання	Множення
0 + 0 = 0	0*0 = 0
0+1 = 1	1*0 = 0
1+0 = 1	0*1=0
1 + 1 = 10	1*1 = 1

Користуючись цими правилами, отримуємо:

Приклади

Додавання

  100      101                  110                      111

⁺    1 ⁺     1 ⁺      1  ⁺      1

  101      110                   111                   1000

Множення

       100                     101

       ^х    11  ^х   10

       100                     000

       ⁺  100                  ⁺  101

     1010                   1010

 

IV. Застосування знань, умінь і навичок

Завдання 1.  Подайте  у десятковій  системі числа:

11011010₂,     3В5D₁₆,    203₈

Завдання 2.  В саду росте 40 фруктових дерев: 34 яблуні і 4 груші. В якій системі пораховано дерева?

(Відповідь: 40=34+4, ця рівність справджується в системі з основою х, тобто 40_х=34_х+4_х;   4*х¹ + 0*х⁰ = 3*х¹ + 4*х⁰ + 4*х⁰;   4х=3х+4+4;   х=8.)

Завдання 3.  Замість «?» поставте 1 або 0 так, щоб число зліва було найбільшим, а число справа – найменшим.

1 ? ? 1;         1 1 0 1;     1 ? ? 1

Завдання 4.  У десятковій системі числення знайдіть 20% від числа 1000001, заданого у двійковій системі.

(Відповідь: 100001₂=1*2⁶ +  0*2⁵ + 0*2⁴ + 0*2³ + 0*2² + 0*2¹ + 1*2⁰ = 65;    65*20/100=13)

Завдання 5.  Знайти в десятковій системі числення гіпотенузу С трикутника, катети якого відповідно рівні А = 110₂; В =1000₂ 

(Відповідь: А = 6; В = 8; С²=А²+В²= 36 + 64 = 100; С = 10)

Завдання 6.  Бізнесмен Рябошапка привіз на планету Альфа 10000 пачок сірників по 2 грн. за пачку. На планеті користуються 16-ю системою числення. Рябошапка продав весь товар по 2 альфи за пачку і обміняв їх на гривні по курсу один до одного. Який прибуток отримав бізнесмен?

(Відповідь: 10000*2=20000;  20000₁₆= 2*16⁴ + 0*16³ + 0*16² + 0*16¹ + 0*2⁰ = 131072₁₀;    131072 – 20000=111072)

V. Підбиття підсумків уроку

VІ. Домашнє завдання

Скласти таблиці відповідності цифр вісімкової системи цифрам двійкової системи.